随机变量的概念

随机变量概念的引入是很重要的,由于引入了随机变量,数学分析的方法就可用来研究随机现象了。

离散型随机变量
离散型随机变量:
只能取有限个值或可列无穷多个值的随机变量X称之为离散型随机变量
概率分布列

分布列的性质:
0—1分布(伯努利分布、两点分布)

二项分布
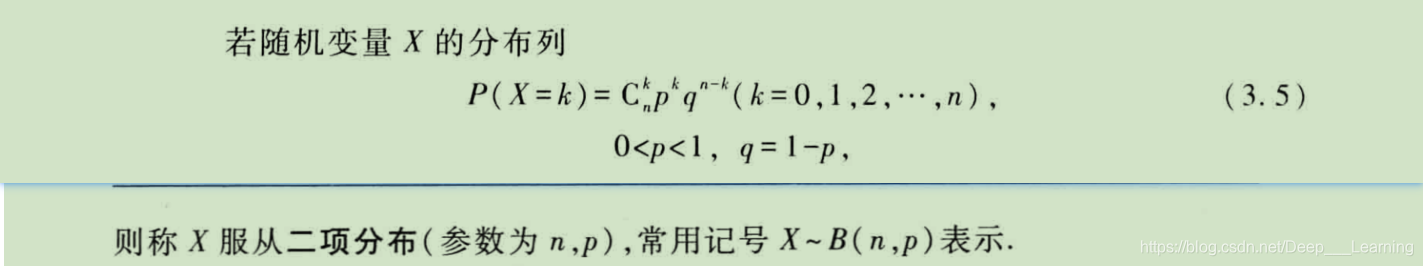
性质:

泊松分布

几何分布
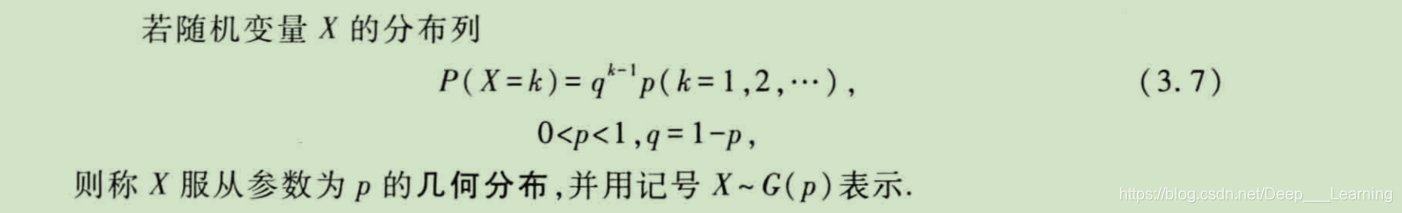
性质:
几何分布具有无记忆性
超几何分布

由此可见,二项分布可以用来描述有放回抽样,而超几何分布可用来描述不放回抽样。

随机变量的分布函数

性质

连续型随机变量


概率密度 f ( x ) f(x) f(x)的数值反映了随机变量X取x的邻近值的概率的大小。
注意:对连续型随机变量而言,概率 P ( X = x ) P(X=x) P(X=x)不能描述X取x值的概率分布规律,因为对任何x值,总有 P ( X = x ) = 0 P(X=x)=0 P(X=x)=0
由于连续型随机变量取个别值的概率为0,因此想用列举连续型随机变量取某个值的概率来描述这种随机变量不但做不到,而且也毫无意义。
此外,当计算连续型随机变量落在某一区间的概率时,区间是否包含端点,是无需考虑的。
一个事件的概率等于零,这件事并不一定是不可能事件;同样一个事件的概率等于1,这事件也未必是必然事件。
均匀分布

X落在子区间上的概率与子区间的长度成正比,而与子区间的位置无关,属于几何分布。故X落在长度相等的各个子区间的可能性是相等的。
“均匀分布”中的“均匀”的含义就是“等可能”的意思
指数分布
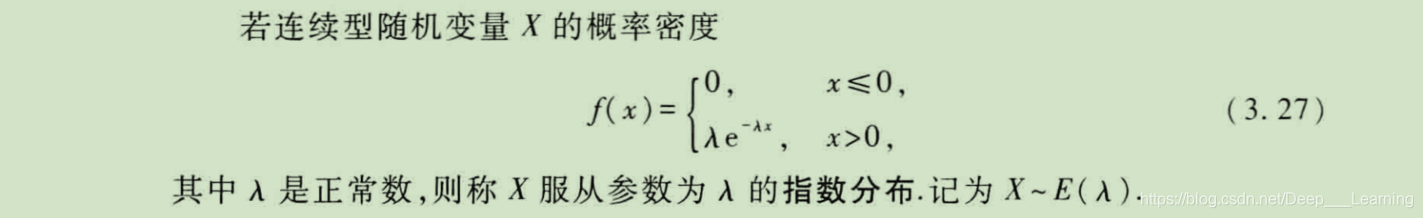
指数分布常用来近似表示各种寿命的分布
指数分布具有类似于几何分布的无记忆性
正态分布
连续型随机变量中,最重要的分布是正态分布,也称高斯分布。

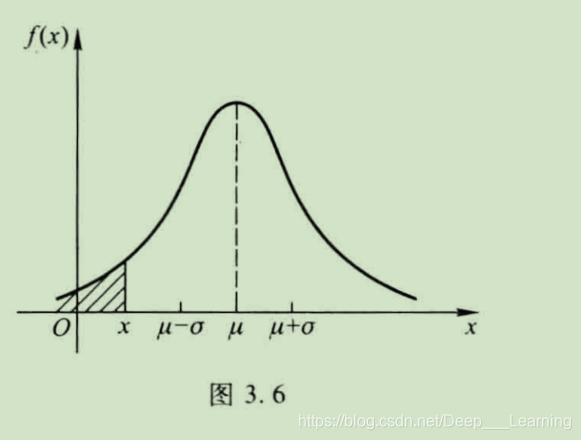
当 固 定 σ 值 而 改 变 μ 值 时 , f ( x ) 的 图 形 将 随 着 μ 值 的 增 大 而 沿 着 x 轴 向 右 平 移 , 且 不 改 变 其 形 状 ; 当固定\sigma值而改变\mu值时,f(x)的图形将随着\mu 值的增大而沿着x轴向右平移,且不改变其形状; 当固定σ值而改变μ值时,f(x)的图形将随着μ值的增大而沿着x轴向右平移,且不改变其形状;
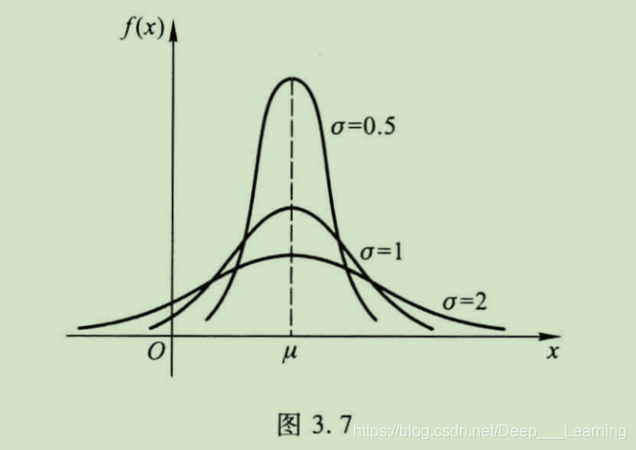
当 固 定 μ 值 而 改 变 σ 值 时 , f ( x ) 的 图 形 将 随 着 σ 值 的 减 少 而 越 变 越 陡 峭 , 且 对 称 中 心 不 变 。 当固定\mu 值而改变\sigma 值时,f(x)的图形将随着\sigma 值的减少而越变越陡峭,且对称中心不变。 当固定μ值而改变σ值时,f(x)的图形将随着σ值的减少而越变越陡峭,且对称中心不变。
标准正态分布:
若
正
态
分
布
N
(
μ
,
σ
2
)
中
参
数
μ
,
σ
分
别
为
0
,
1
时
,
则
得
到
N
(
0
,
1
)
,
此
称
为
标
准
正
态
分
布
。
若正态分布N(\mu ,\sigma^2)中参数\mu ,\sigma 分别为0,1时,则得到N(0,1),此称为标准正态分布。
若正态分布N(μ,σ2)中参数μ,σ分别为0,1时,则得到N(0,1),此称为标准正态分布。
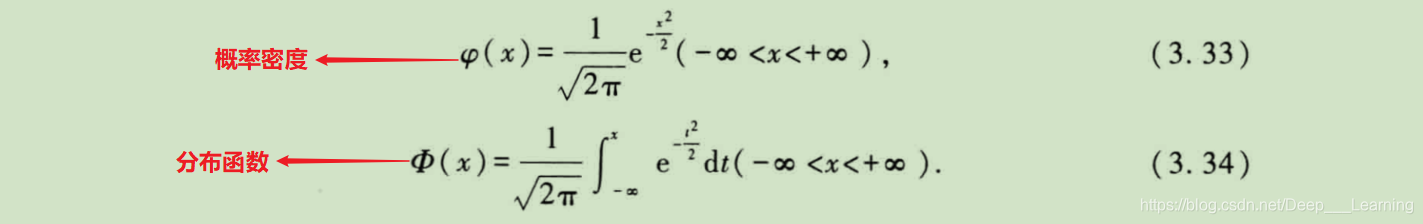
一般正态分布的分布函数与标准正态分布的分布函数,有下面的关系:
F ( x ) = Φ ( x − μ σ ) F(x)=\Phi(\frac {x-\mu} \sigma) F(x)=Φ(σx−μ)
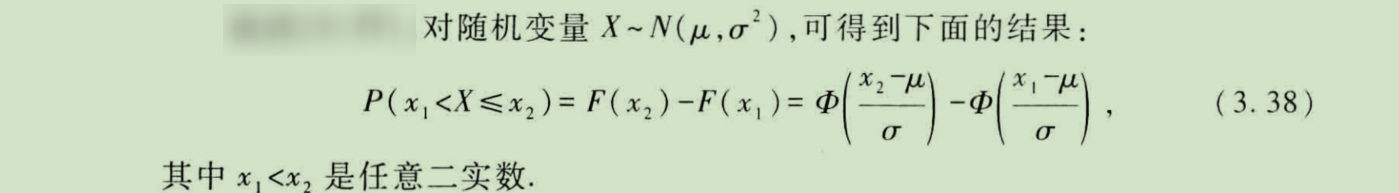
随机变量的函数分布

当X为离散型随机变量时,g(X)的分布可直接由X的分布列求得。
























 491
491

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








