高效解决数论和数组问题的算法实践-优快云博客

1. 两数之和

TwoSum

时间：O（n）来自遍历整个数组，每次遍历都查找一次hashset用时O（1）空间：O（n）来自hashset存储之前遍历过的元素

重点在这一段：Hashset
对于每一个遍历的元素num，都在之前遍历过的并存入map中的元素们中找有没有target - num，如果有，返回[hashtable[target - num], i], 如果没有，将当前遍历的元素以（key，value） = （nums[i], i）的形式存入map。

if target - num in hashtable:
                return [hashtable[target - num], i]
            hashtable[nums[i]] = i

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hashtable = dict() # key: nums[i] value: i
        for i, num in enumerate(nums):
            if target - num in hashtable:
                return [hashtable[target - num], i]
            hashtable[nums[i]] = i
        return []

Two Sum II - Input array is sorted

时间：O（n）来自双指针搜索空间：O（1）不需要开辟额外空间
双指针

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        n = len(numbers)
        i, j = 0, n - 1;
        while i < j:
            if numbers[i] + numbers[j] == target:
                return [i + 1, j + 1]
            elif numbers[i] + numbers[j] < target:
                 i += 1
            else:
                 j -= 1
        return [-1, -1]

Two Sum IV - Input is a BST
时间：O（2n），来自中序遍历BST和双指针搜索空间：O（n）来自list存储正序list

方法1：BST中序遍历生成有序list+双指针

class Solution:
    def findTarget(self, root, k):
        def inorder(root1, list1):
            if root1 is None:
                return
            inorder(root1.left, list1)
            list1.append(root1.val)
            inorder(root1.right, list1)
        elements = []
        inorder(root, elements)
        i, j = 0, len(elements) - 1
        while i < j:
            two_sum = elements[i] + elements[j]
            if two_sum == k:
                return True
            elif two_sum < k:
                i += 1
            else:
                j -= 1
        return False

方法2：HashSet + 二叉树遍历
时间：O（n）遍历二叉树的每一个点空间：O（n）来自set存储遍历过的节点值

新建set：空set用set(), 非空可以用{…}。
在每个node都进行一下这一段，和使用HashMap解TwoSum是一样的。对于每一个遍历的元素num，都在之前遍历过的并存入map中的元素们中找有没有target - num，如果有，返回True, 如果没有，将当前遍历的元素以（value） = （root.val）的形式存入set。遍历完整棵树后，如果这棵树中有某节点的find返回的是True，那么这棵树self.find(root, hashset, k)就会返回True。

if target - root.val in hashset:
            return True
        else:
            hashset.add(root.val)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findTarget(self, root, k):
        if root is None:
            return False
        hashset = set()
        return self.find(root, hashset, k)
    def find(self, root, hashset, target):
        if root is None:
            return False
        if target - root.val in hashset:
            return True
        else:
            hashset.add(root.val)
        return self.find(root.left, hashset, target) or self.find(root.right, hashset, target)

Two Sum BSTs（两棵树，各取一个点，求和=target，有则返回True）
时间：O（nlogn）空间：O（logn）来自递归栈
遍历其中一棵BST1,遍历到每个结点的时候，取出该结点值node.val，求得(target-node.val)的值拿到BST2去查找，找到就返回true。（O（logn））若同步步骤1没找到，则递归遍历BST1的左子树和BST1的右子树，不断执行步骤1，直到找到或者所有节点遍历完也未找到为止。（O（n））

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def twoSumBSTs(self, root1: TreeNode, root2: TreeNode, target: int) -> bool:
        def find(root, target1) -> bool:
            if root is None:
                return False
            if root.val == target1:
                return True
            elif root.val > target1:
                return find(root.left, target1)
            else:
                return find(root.right, target1)
        if root1 is None:
            return False
        if find(root2, target - root1.val):
            return True
        else:
            return self.twoSumBSTs(root1.left, root2, target) or self.twoSumBSTs(root1.right, root2, target)

Two Sum III - Data structure design

相当于设计一个HashMap，在python中是dict，key = 元素值，value = 该元素值出现次数。时间复杂度：<= O(n), 空间：O（1）

方法1：HashMap
这个数据结构的方法包括：
1）初始化一个空map

def __init__(self):
        """
        Initialize your data structure here.
        """
        self.numbers = {}

2）add number in this map

def add(self, number: int) -> None: # O(1)
        """
        Add the number to an internal data structure..
        """
        # 添加一个元素，如果键值原本存在，就value+1， 如果不存在，用self.numbers[number] = 1
        if number not in self.numbers:
            self.numbers[number] = 1
        else:
            self.numbers[number] += 1

java写法：

nums.put(number, nums.getOrDefault(number, 0) + 1);

3）找map中有没有两个数相加 = target

def find(self, value: int) -> bool: # O(n)
        """
        Find if there exists any pair of numbers which sum is equal to the value.
        """
        for key in self.numbers:
            key2 = value - key
            if key2 in self.numbers:
                if self.numbers[key2] >= 1 and key != key2:
                    return True
                elif self.numbers[key2] > 1 and key == key2:
                    return True
        return False

java写法：

public boolean find(int value) { // O(n)
        for (Integer num : nums.keySet()) {
            int target = value - num;
            if (target == num && nums.get(target) > 1) return true;
            if (target != num && nums.containsKey(target)) return true;
        }
        return false;
    }

方法2：排序+双指针
时间复杂度：>=O(nlogn) 空间：O（n）

public class TwoSum {
    private List<Integer> nums;
    private boolean isSorted;

    public TwoSum() {
        nums = new ArrayList<>();
        isSorted = false;
    }

    // 添加一个元素
    public void add(int number) {
        nums.add(number); // O(1)
        isSorted = false;
    }

    // 查找是否存在两个数，这两个数的和等于 value
    public boolean find(int value) { // O(nlogn)
        if (!isSorted) {
            Collections.sort(nums); // O(nlogn)
            isSorted = true;
        }

        int left = 0;
        int right = nums.size() - 1;
        while (left < right) { // O(n)
            int sum = nums.get(left) + nums.get(right);
            if (sum == value) {
                return true;
            } else if (sum < value) {
                left++;
            } else {
                right--;
            }
        }

        return false;
    }
}

关于python字典的知识点：

1）遍历方式：

1、遍历key值，value值（下面写法完全等价）：
a = {'a': '1', 'b': '2', 'c': '3'}
方式一：
for key in a:
    print(key+':'+a[key])
方式二：
for key in a.keys():
    print(key+':'+a[key])
方式三：
for key,value in a.items():
       print(key+':'+value)
方式四：
for (key,value) in a.items():
    print(key+':'+value)
打印结果：
a:1
b:2
c:3
 
2、遍历value值：
for value in a.values():
    print(value)
打印结果：
1
2
3
 
3、遍历字典项
for kv in a.items():
    print(kv)
打印结果：
('a', '1')
('b', '2')
('c', '3')

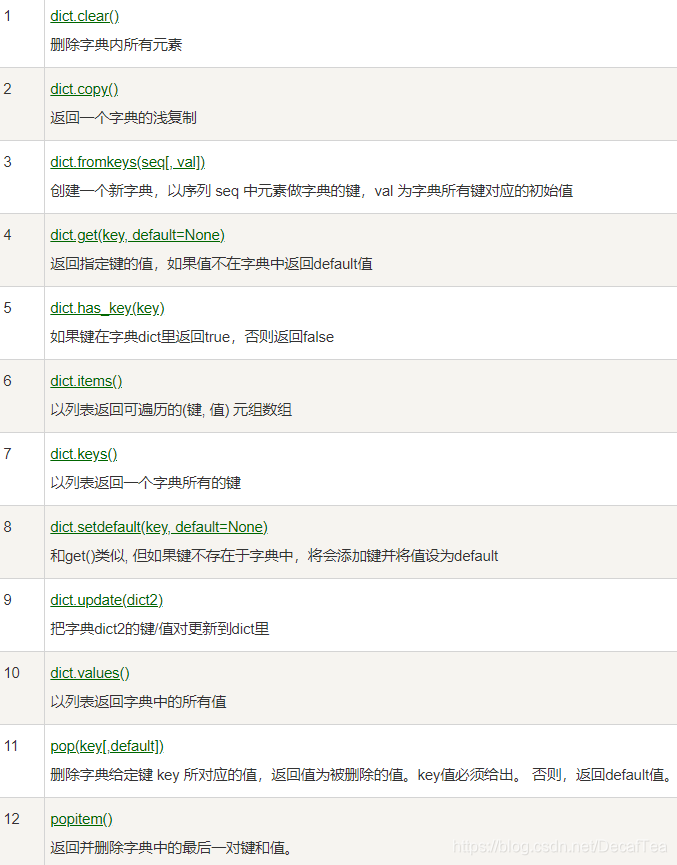
2）方法

在这里插入图片描述

2. 三数之和

返回所有满足三数之和 = 0的unique三元组，返回值是list[list[int]]形式
双指针问题，首先对数组进行排序，然后遍历每一个值作为固定值，之后用双指针左右遍历。

时间复杂度：O（n²) 遍历a+双指针bc
空间复杂度：O（1）原地

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        n=len(nums)
        res=[]
        # 特判直接返回的情况
        if(not nums or n<3):
            return []
        nums.sort()
        for i in range(n-2):
            # 因为数组已经排序，所以a < b < c， 如果a > 0, 那么三数之和不可能=0
            if(nums[i]>0):
                return res
            # 去重
            if(i>0 and nums[i]==nums[i-1]):
                continue
            L = i + 1
            R = n - 1
            while(L < R):
                if(nums[i]+nums[L]+nums[R]==0):
                    res.append([nums[i],nums[L],nums[R]])
                    # 去重
                    while(L<R and nums[L]==nums[L+1]):
                        L=L+1
                    while(L<R and nums[R]==nums[R-1]):
                        R=R-1
                    L=L+1
                    R=R-1
                elif(nums[i]+nums[L]+nums[R]>0):
                    R=R-1
                else:
                    L=L+1
        return res

返回最接近target的三数之和
您可以假设每个输入都只有一个解。which means 不用去重。
双指针问题，首先对数组进行排序，然后遍历每一个值作为固定值，之后用双指针左右遍历。

剪枝：
第一个数去重
如果最大的数都小于等于target，那直接下一轮，first往右也许能更大；如果最小的数都大于等于target，那压根别找了，因为不可能再有更小的数了，直接Break掉返回结果即可。

def threeSumClosest(self, nums: List[int], target: int) -> int:
        n=len(nums)
        # 特判直接返回的情况
        if(not nums or n<3):
            return None
        nums.sort()
        res=float("inf") # 存“最接近和”
        for i in range(n):
        	# 剪枝，优化时间复杂度
            if(i>0 and nums[i]==nums[i-1]): # 第一个数去重
                continue
            max_sum = nums[first] + nums[-2] + nums[-1]
            min_sum = nums[first] + nums[first + 1] + nums[first + 2]
            if max_sum <= target:    # 最大的数
                if abs(max_sum - target) < abs(ans - target):
                    ans = max_sum
                continue              
            elif min_sum >= target:  # 最小的数
                if abs(min_sum - target) < abs(ans - target):
                    ans = min_sum      
                break   
                
			# 双指针遍历第二第三个数
			L=i+1
            R=n-1
            while(L<R):
                cur_sum=nums[i]+nums[L]+nums[R]
                
                if(cur_sum==target): # sum = target直接返回了！
                    return target
                if(abs(cur_sum-target)<abs(res-target)): # 更新最接近和res
                    res=cur_sum
                if(cur_sum-target<0): # 移动双指针
                    L+=1
                else:
                    R-=1
        return res

3. 四数之和

返回所有满足四数之和 = target的unique四元组，返回值是list[list[int]]形式。

剪枝：
1）第1、2、3、4个数去重
2）在这里插入图片描述

class Solution:
    def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
        quadruplets = list()
        # 特判直接返回的情况
        if not nums or len(nums) < 4:
            return quadruplets
        
        nums.sort()
        length = len(nums)
        for i in range(length - 3):
            if i > 0 and nums[i] == nums[i - 1]: # 第一个数去重
                continue
            # 剪枝
            if nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target:
                break
            if nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target:
                continue
            for j in range(i + 1, length - 2):
                if j > i + 1 and nums[j] == nums[j - 1]: # 第二个数去重
                    continue
                # 剪枝
                if nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target:
                    break
                if nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target:
                    continue
                left, right = j + 1, length - 1
                while left < right:
                    total = nums[i] + nums[j] + nums[left] + nums[right]
                    if total == target:
                        quadruplets.append([nums[i], nums[j], nums[left], nums[right]])
                        while left < right and nums[left] == nums[left + 1]: # 第三个数去重
                            left += 1
                        left += 1
                        while left < right and nums[right] == nums[right - 1]: # 第四个数去重
                            right -= 1
                        right -= 1
                    # 移动双指针
                    elif total < target:
                        left += 1
                    else:
                        right -= 1
        
        return quadruplets