MATLAB专题2 特殊矩阵及其应用-优快云博客

本文链接：https://blog.youkuaiyun.com/Davidmyhmyh/article/details/145238111

一、特殊矩阵

1.一些基础又典型矩阵

ones(n):n阶方阵，所有元素为1

zeros(n):n阶方阵，所有元素为0

eye(n):n阶单位矩阵

2.幻方矩阵

通常使用magic(n)生成幻方矩阵，其中n为矩阵的行数或者列数

最常见的为3阶幻方，其共有15种，且每行每列以及两条对角线上数的和均为15

3.对角矩阵

对角矩阵：非零元素仅仅存在于对角线上

其中标题矩阵要求对角线上的值一样，单位矩阵要求对角线上的值一样且都为1

4.三角矩阵

使用triu和tril函数分别提取某一个矩阵的上三角部分以及下三角部分

A=ones(3);
B=triu(A);
C=tril(A);

5.帕斯卡矩阵

可以理解为杨辉三角逆时针旋转 $\frac{\pi}{4}$ 后得到的矩阵

6.利用与随机数有关的函数生成矩阵

A=fix(10+(99-10+1)*rand(5));
B=0.6+sqrt(0.1)*randn(5);
C=eye(5);

其中rand常生成（0,1）中的均匀分布随机数或方阵

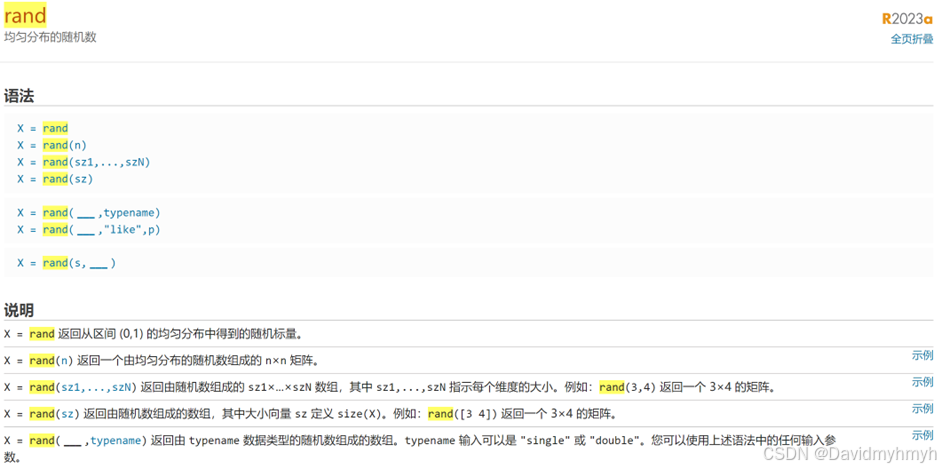
randi常生成特定闭区间[a,b]内的随机数或者方阵

randn生成标准正态分布下产生的随机数或者其组成的方阵，其中期望为0，方差为1

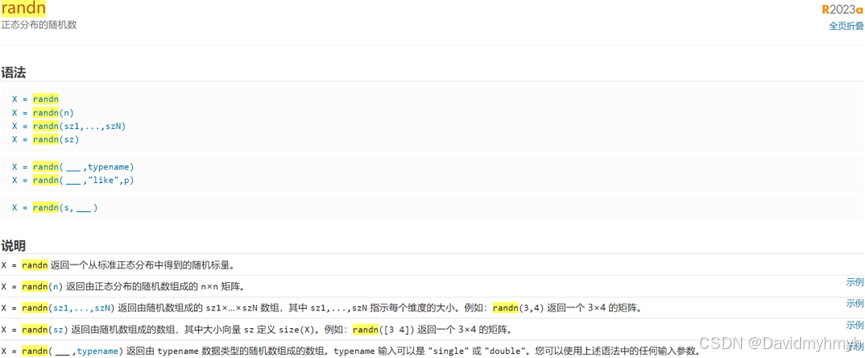
二、旋转与翻转操作

旋转：常用rot90函数，对矩阵进行特定次数的逆时针旋转。需明确旋转的矩阵以及旋转的次数

A = [1 2 3; 4 5 6; 7 8 9];

B1 = rot90(A);

B2 = rot90(A, 2);

B3 = rot90(A, 3);

B4 = rot90(A, 0);

翻转：flip(上下左右都翻转）

flipud(只上下翻转）

fliplr(只左右翻转）

三、矩阵的稀疏存储

sparse:记非零元素的位置与值 A=sparse(S) VS S=full(A)

经典函数：

sparse函数：

sparse(m,n):即zeros(m,n)

也可单独规定非零元素（按row→column→value的顺序）

D=sparse([1,2,3],[2,3,4],[9,3,7]);

输出得到

2.spconvert(A)

例子如下：每行前两个元素为下标，第三个元素为元素值

A=[1,2,3;8,9,3;1,6,4];

B=spconvert(A);

输出得到

四、应用：图像的处理

核心：利用数值矩阵处理图片

黑白图片：0代表黑色，1代表白色

灰度图：0代表黑色，255代表白色，其中有255种不同灰度

彩色图：像素值→RGB值

下标图：每个下标代表一种映射，反映相关信息

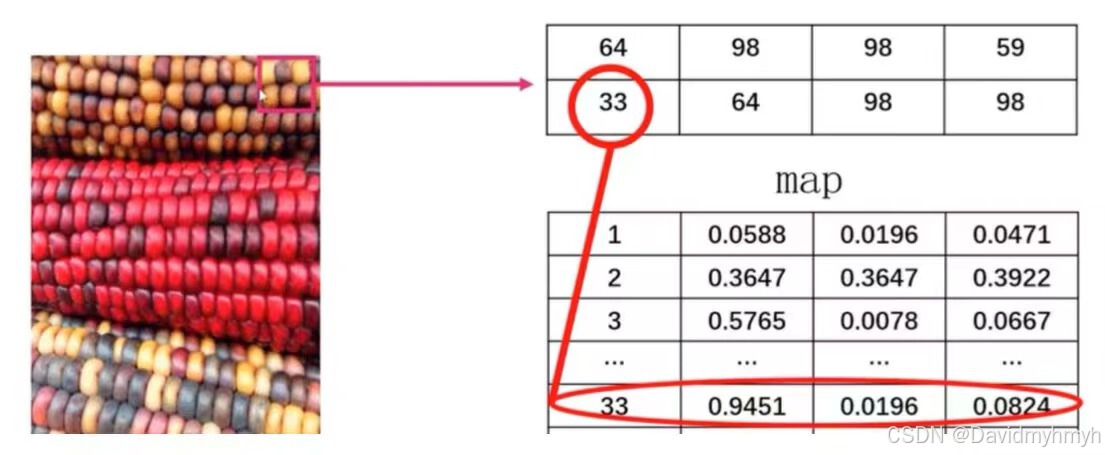
A=imread('rabbit.jpg');
B=rgb2gray(A); 
figure;
subplot(1,2,1);
imshow(A);
subplot(1,2,2);
imshow(B);

经典步骤：imread读取图片，读取后进行处理（(rgb,ind,gray,bw)→(rgb,ind,gray,bw)），最后用imshow展示图片