【打CF，学算法——五星级】CodeForces 478D (dp计数)

最新推荐文章于 2021-01-14 21:46:36 发布

David_Jett

最新推荐文章于 2021-01-14 21:46:36 发布

阅读量934

点赞数 1

分类专栏： CodeForces 编程题——动态规划【打CF，学算法】文章标签： codeforces 动态规划

本文链接：https://blog.youkuaiyun.com/David_Jett/article/details/51887089

版权

CodeForces 同时被 3 个专栏收录

50 篇文章

订阅专栏

【打CF，学算法】

49 篇文章

订阅专栏

编程题——动态规划

27 篇文章

订阅专栏

本文详细介绍了如何利用动态规划解决CodeForces 478D问题，即用红绿两种方块构建特定规则的塔并计算不同构造方法的数量。通过分析问题，确定最高层数，并使用滚动数组优化空间复杂度，最终求得符合条件的塔的构建方法数量模10^9 + 7的结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【CF简介】

提交链接：CF 478D

题面：

There are r red and g green blocks for construction of the red-green tower. Red-green tower can be built following next rules:

Red-green tower is consisting of some number of levels;
Let the red-green tower consist of n levels, then the first level of this tower should consist of n blocks, second level — of n - 1 blocks, the third one — of n - 2 blocks, and so on — the last level of such tower should consist of the one block. In other words, each successive level should contain one block less than the previous one;
Each level of the red-green tower should contain blocks of the same color.

$\text{[math]}$

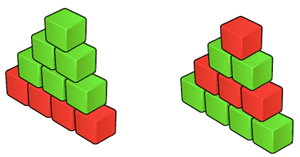
Let h be the maximum possible number of levels of red-green tower, that can be built out of r red and g green blocks meeting the rules above. The task is to determine how many different red-green towers having h levels can be built out of the available blocks.

Two red-green towers are considered different if there exists some level, that consists of red blocks in the one tower and consists of green blocks in the other tower.

You are to write a program that will find the number of different red-green towers of height h modulo 10⁹ + 7.

Input

The only line of input contains two integers r and g, separated by a single space — the number of available red and green blocks respectively (0 ≤ r, g ≤ 2·10⁵, r + g ≥ 1).

Output

Output the only integer — the number of different possible red-green towers of height h modulo 10⁹ + 7.

Examples

Input

4 6

Output

Input

9 7

Output

Input

1 1

Output

Note

The image in the problem statement shows all possible red-green towers for the first sample.

题意：

给定红绿两种方块，要求以1，2，3..n的方式，一层一层垒上去，且任意一层只能是单色，问在该种方式下垒到最高高度的方式有多少种？

解题：

因为是1，2，3..所以只要刚刚好方块够到某一层的总数量的话，是一定可以构造出可行方案的，因此可以直接根据两种方块数量总和，先求出最高高度。根据范围，最高高度为1000。可以比较轻松地想到用dp[i][j]来表示，其中i为第几层,j为到该层为止用了多少红色方块，dp的值的含义是在第i层用了j块红色方块的方案数。此方法看似可行，实则不然，1000*（2*10^5）远超出题目给的空间限定范围，且复杂度也够呛。因为，我们最后要取的仅仅是最后一层的结果，前面的计算过程都是不需要的，因此，我们可以采用滚动数组的方法，将第一维压缩至2，分别表示上一层和下一层。在计算过程中用队列或其他数据结构保存要更新的点。最后取最后一层的所有结果和即可。

代码：

#include <iostream>
#include <string>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <vector>
#define LL long long
#define maxn 200010
#define sq(a)  1LL*(a)*(a)
#define mod 1000000007
using namespace std;
bool vis[maxn];
vector <int> v[2];
int amount[1000];
int dp[2][maxn];
void init()
{
	for(int i=1;i<1000;i++)
		amount[i]=(1+i)*i/2;
}
int main()
{
	int r,g,total,h,a,b,sz,tmp,ans=0,tmp2;
	init();
	scanf("%d%d",&r,&g);
    total=r+g;
    h=(-1+sqrt(1+8.0*total))/2;
	if(g>0)
	{
		dp[0][0]=1;
		v[0].push_back(0);
	}
	if(r>0)
	{
		dp[0][1]=1;
		v[0].push_back(1);
	}

	a=0;
	b=1;
	for(int i=2;i<=h;i++)
	{
	   sz=v[a].size();
	   for(int i=0;i<sz;i++)
		   vis[v[a][i]]=0;
	   for(int j=0;j<sz;j++)
	   {

		   tmp=amount[i]-v[a][j];
		   if(tmp<=g)
		   {
			   if(!vis[v[a][j]])
			   {
				   v[b].push_back(v[a][j]);
				   dp[b][v[a][j]]=0;
				   vis[v[a][j]]=1;
			   }
			   dp[b][v[a][j]]=(dp[b][v[a][j]]+dp[a][v[a][j]])%mod;
		   }
		   tmp=v[a][j]+amount[i]-amount[i-1];
           if(tmp<=r)
		   {
			   if(!vis[tmp])
			   {
				   v[b].push_back(tmp);
				   vis[tmp]=1;
				   dp[b][tmp]=0;
			   }
			   dp[b][tmp]=(dp[b][tmp]+dp[a][v[a][j]])%mod;
		   }
		 }
	   v[a].clear();
	   swap(a,b);
	}
	sz=v[a].size();
	for(int i=0;i<sz;i++)
		ans=(ans+dp[(h+1)%2][v[a][i]])%mod;
	printf("%d\n",ans);
	return 0;
}