菱形继承和组合与继承的选择。

最新推荐文章于 2025-03-21 18:54:24 发布

GXR_1116

最新推荐文章于 2025-03-21 18:54:24 发布

阅读量145

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/Darling_sheeps/article/details/88766649

本文介绍了单继承、多继承和菱形继承的概念，并详细解析了菱形继承中的二义性问题及解决方案。通过虚拟继承解决了数据冗余问题，并对比了继承与组合的不同应用场景。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

单继承：一个子类只有一个直接父类的继承关系。
多继承：一个子类有两个或两个以上的直接父类的继承关系。
菱形继承：是多继承的一种特殊情况。

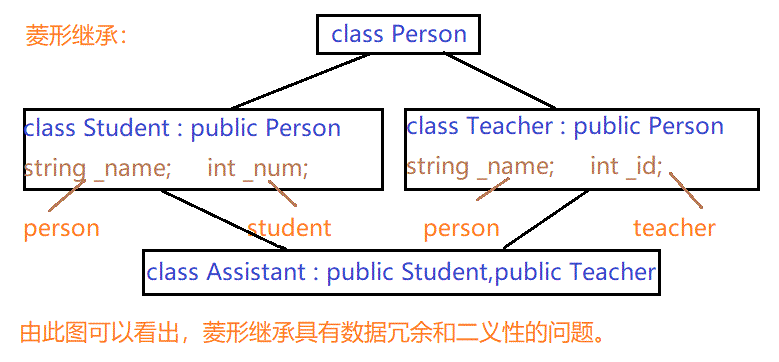
菱形继承问题的具体分析：

class Person{
  public:
     string _name;
}
class Student : public Person{
  protected:
     int _num;
}
class Teacher : public Person{
  protected:
     int _id;
}
class Assistant : public Person,public Student{
  protected:
     string _major;
}
void Test1(){
  Assistant a;
  a._name = "XiaoHua";
}

由上述的代码中可以看出，在给a._name初始化的时候，不确定访问的是Teacher中的_name，还是Student中的_name。
为了解决二义性的问题，我们可以指定访问父类的成员。

a.Student::_name = "XiaoHua";
a.Teacher::_name = "XiaoHua";

但是，这种方法没有办法解决数据冗余的问题，因此只能用虚拟继承来实现(添加关键字virtual)。

class Student : virtual public Person{
  protected:
     int _num;
}
class Teacher : virtual public Person{
  protected:
     int _id;
}

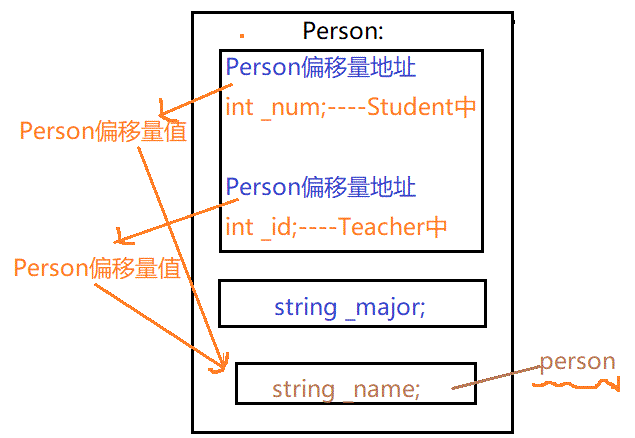
其实，菱形虚拟继承的原理是：通过了Student和Teacher的两个指针指向的一张表。这两个指针叫虚基表指针，这两个表叫虚基表。续集表中存在偏移量，通过偏移量可以找到下面的_name。
在这里插入图片描述

关于继承和组合： public继承是一种is-a的关系；组合是一种has-a的关系。

class Eye{
  public:
    void Look(void);
}
继承：
class Head : public Eye{};
组合：
class Head{
  Eye _eye;
}

虽然继承和组合都实现了复用，但是优先使用组合。
原因是：在继承方式中，基类的内部细节对子类可见，一定程度上破坏了基类的封装。派生类和基类之间的依赖关系很强，耦合度高；
而在组合中，对象内部的细节是不可见的。组合类之间没有很强的依赖关系，耦合度低。