模拟测试9题解-优快云博客

本文链接：https://blog.youkuaiyun.com/Daniel__d/article/details/102810297

本文详细解析了模拟测试9中的三道题目，包括数列、数对和最小距离问题的算法实现，使用拓展欧几里得算法、动态规划与线段树优化、多源点最短路径等技术。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

191029-模拟测试9

T1 数列

解析

一眼 拓展欧几里得算法（实际花了一个小时看出来，而且发现自己写不来）
话归正传，我们已经求出一组解了，那么如何去找到 $∣ x ∣ + ∣ y ∣$ 的最小值呢，~~我反正是枚举取最小，然后t了~~ 不过，可以打个表来观察，发现min值=min（x=最小正数时的解，x=最大负数时的解）；（x为一次项系数较小的那个自变量，~~话说为这个我调了好久~~ ）

题解

#include<bits/stdc++.h>
using namespace std;
long long a,b,d,k,n,x,y,ans;
void exgcd(long long a,long long b,long long &x,long long &y)
{
	if(b==0)
	{
		x=1;
		y=0;
		return;
	}
	exgcd(b,a%b,x,y);
	long long t=x;
	x=y;
	y=t-(a/b)*y;
}
int gcd(int xx,int yy){return (yy==0)?xx:gcd(yy,xx%yy);}
int main()
{
	//freopen("array.in","r",stdin);
	//freopen("array.out","w",stdout);
	scanf("%lld%lld%lld",&n,&a,&b);
	if(a>b) swap(a,b);
	d=gcd(a,b);
	a/=d;
	b/=d;
	exgcd(a,b,x,y);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&k);
		k=abs(k);
		if(k%d) 
		{
			printf("-1\n");
			return 0;
		}
		k/=d;
		long long tx=x*(k);
		long long ty=y*(k);
		if(tx>0)
			ans+=min(abs(tx-(tx/b)*b)+abs(ty+(tx/b)*a),abs(tx-(tx/b)*b-b)+abs(ty+(tx/b)*a+a));
		else
			ans+=min(abs(tx+(-tx/b)*b)+abs(ty-(-tx/b)*a),abs(tx+(-tx/b)*b+b)+abs(ty-(-tx/b)*a-a));
	}
	printf("%lld",ans);
	return 0;
}

T2 数对

解析

个人觉得是三道中最难的那一道，~~话说我考场上写了个随机化贪心，全wa~~
话归正传，首先很明显dp，但是我们需要将每个数对按照每种法则来排序，来看下面四种情况
1, $a_i<b_j,b_i<a_j$ 很明显我们需要将j数对放在i数对后面
2, $a_i>b_j,b_i>a_j$ 与上面情况相反
3, $a_i>b_j,b_i<a_j$ 该种情况下，i，j的顺序没有限制
4, $a_i<b_j,b_i>a_j$ 同上
因此我们可以将整个序列按** $a + b$ **的大小，来排序，最后再线段树优化dp
~~没学过线段树优化dp~~ ，所以想了好久，解析见下图：

题解

#include<bits/stdc++.h>
#define int long long
#define M 200005
using namespace std;
int w[M*2],n,m,len;
struct zb
{
	int x,y,z;
}a[M];
struct node
{
	int l,r,maxn,add;
}tree[M*4];
bool comp(const zb &a,const zb &b)
{
	return a.x+a.y<b.x+b.y;
}
void build(int id, int l, int r)
{
	tree[id].l = l;
	tree[id].r = r;
	if(l==r)
		return;
	int mid = (l + r) >> 1;
	build(id<<1, l, mid);
	build(id<<1|1, mid + 1, r);
}
void pushdown(int k)
{
	if(tree[k].l!=tree[k].r)
	{
		tree[k<<1].add+=tree[k].add;
		tree[k<<1|1].add+=tree[k].add;
		tree[k<<1].maxn+=tree[k].add;
		tree[k<<1|1].maxn+=tree[k].add;
		tree[k].add=0;
	}
}
void update(int k,int l,int r,int val)
{
	pushdown(k);
	if(tree[k].l>=l&&tree[k].r<=r) 
	{
		tree[k].add+=val;
		tree[k].maxn+=val;
		return;
	}
	int mid=(tree[k].l+tree[k].r)>>1;
	if(l<=mid) update(k<<1,l,r,val);
	if(r>mid) update(k<<1|1,l,r,val);
	tree[k].maxn=max(tree[k<<1].maxn,tree[k<<1|1].maxn);
}
void maxx(int k,int pos,int val)
{
	pushdown(k);
	if(tree[k].l==tree[k].r)
	{
		tree[k].maxn=max(tree[k].maxn, val);
		return;
	}
	int mid=(tree[k].l+tree[k].r)>>1;
	if(pos<=mid) maxx(k<<1,pos,val);
	else maxx(k<<1|1,pos,val);
	tree[k].maxn=max(tree[k<<1].maxn,tree[k<<1|1].maxn);
}
int query(int k,int l,int r)
{
	pushdown(k);
	if(tree[k].l>=l&&tree[k].r<=r) return tree[k].maxn;
	int mid=(tree[k].l+tree[k].r)>>1;
	pushdown(k);
	int ret=0;
	if(l<=mid) ret=max(ret,query(k<<1,l,r));
	if(r>mid) ret=max(ret,query(k<<1|1,l,r));
	return ret;
}
signed main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld%lld%lld",&a[i].x,&a[i].y,&a[i].z);
		w[++m]=a[i].x;
		w[++m]=a[i].y;
	}
	sort(w+1,w+m+1);
	len=unique(w+1,w+m+1)-w-1;
	for(int i=1;i<=n;i++)
	{
		a[i].x=lower_bound(w+1,w+len+1,a[i].x)-w;
		a[i].y=lower_bound(w+1,w+len+1,a[i].y)-w;
	}
	build(1, 1, len);
	sort(a+1,a+n+1,comp);
	for(int i=1;i<=n;i++)
	{
		maxx(1,a[i].x,query(1,1,min(a[i].x,a[i].y))+a[i].z);
		if(a[i].x<a[i].y)
			update(1,a[i].x+1,a[i].y,a[i].z);
	}
	printf("%lld",tree[1].maxn);
	return 0;
}

T3 最小距离

解析

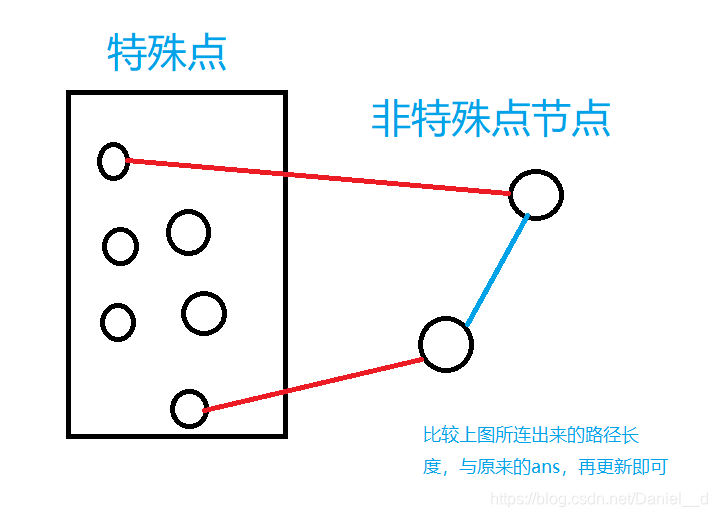
先求一个多源点最短路径，首先新建一个源点为 $n + 1$ ，然后给源点和每个特殊点建一条边权为0的有向边，再跑一遍最短路，同时记录下每个非特殊点节点是被哪个特殊点所拓展的，为from数组（特殊点的from等于本身），然后枚举每一条边，更新答案，详解如下图：

题解

#include<bits/stdc++.h>
#define int long long
#define INF 1e18
#define M 300007
using namespace std;
priority_queue<pair<int,int> >q;
int read()
{
	int f=1;
	int re=0;
	char ch;
	for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
	if(ch=='-')
	{
		f=-1;
		ch=getchar();
	}
	for(;isdigit(ch);ch=getchar())
		re=(re<<3)+(re<<1)+ch-'0';
	return re*f;
}
struct zb
{
	int x,y,z;
}e[200009];
int d[M],tot,to[M*2],nxt[M*2],first[M*2],w[M*2],ans[M],from[M],a[M],n,m,q1,vis[M];
void add(int x,int y,int z)
{
	nxt[++tot]=first[x];
	first[x]=tot;
	to[tot]=y;
	w[tot]=z;
}
void dj(int r)
{
	for(int i=1;i<=n;i++)
		d[i]=INF;
	d[r]=0;
	q.push(make_pair(-d[r],r));
	while(!q.empty())
	{
		int v=q.top().second;
		q.pop();
		if(vis[v]) continue;
		vis[v]=1;
		for(int i=first[v];i;i=nxt[i])
		{
			int u=to[i];
			if(d[u]>d[v]+w[i])
			{
				d[u]=d[v]+w[i];
				from[u]=(from[v])?from[v]:u;
				q.push(make_pair(-d[u],u));
			}
		}
	}
}
signed main()
{
	scanf("%lld%lld%lld",&n,&m,&q1);
	for(int i=1;i<=q1;i++)
	{
		a[i]=read();
		add(n+1,a[i],0);
		ans[a[i]]=INF;
	}
	for(int i=1;i<=m;i++)
	{
		e[i].x=read();
		e[i].y=read();
		e[i].z=read();
		add(e[i].x,e[i].y,e[i].z);
		add(e[i].y,e[i].x,e[i].z);
	}
	dj(n+1);
	for(int i=1;i<=m;i++)
	{
		if(from[e[i].x]!=from[e[i].y])
		{
			ans[from[e[i].x]]=min(ans[from[e[i].x]],d[e[i].x]+d[e[i].y]+e[i].z);
			ans[from[e[i].y]]=min(ans[from[e[i].y]],d[e[i].x]+d[e[i].y]+e[i].z);
		}
	}
	for(int i=1;i<=q1;i++)
		printf("%lld ",ans[a[i]]);
	return 0;
}

扩展

一道与该题类似的题目旅行者

解析

该题只是将双向边改为单向边，所以新建源点的操作和源点连特殊点的操作不变，但是要跑2遍最短路，第一遍是正向边跑，第二遍是建反向边跑，最后与T3类似，枚举每条边来更新答案

题解

#include<bits/stdc++.h>
#define int long long
#define INF 1e18
#define M 1000007
using namespace std;
int read()
{
	int f=1;
	int re=0;
	char ch;
	for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
	if(ch=='-')
	{
		f=-1;
		ch=getchar();
	}
	for(;isdigit(ch);ch=getchar())
		re=(re<<3)+(re<<1)+ch-'0';
	return re*f;
}
struct zb
{
	int x,y,z;
}e[M];
int d2[M],from2[M],d1[M],tot,to[M*2],nxt[M*2],first[M*2],w[M*2],ans[M],from1[M],a[M],n,m,q1,vis[M],t,anss;
bool bj[M];
void add(int x,int y,int z)
{
	nxt[++tot]=first[x];
	first[x]=tot;
	to[tot]=y;
	w[tot]=z;
}
void dj1(int r)
{
	priority_queue<pair<int,int> >q;
	for(int i=1;i<=n+1;i++)
		d1[i]=INF;
	d1[r]=0;
	q.push(make_pair(-d1[r],r));
	while(!q.empty())
	{
		int v=q.top().second;
		q.pop();
		if(vis[v]) continue;
		vis[v]=1;
		for(int i=first[v];i;i=nxt[i])
		{
			int u=to[i];
			if(d1[u]>d1[v]+w[i])
			{
				d1[u]=d1[v]+w[i];
				from1[u]=from1[v]?from1[v]:u;
				q.push(make_pair(-d1[u],u));
			}
		}
	}
}
void dj2(int r)
{
	priority_queue<pair<int,int> >q;
	for(int i=1;i<=n+1;i++)
	{
		vis[i]=0;
		d2[i]=INF;
	}
	d2[r]=0;
	q.push(make_pair(-d2[r],r));
	while(!q.empty())
	{
		int v=q.top().second;
		q.pop();
		if(vis[v]) continue;
		vis[v]=1;
		for(int i=first[v];i;i=nxt[i])
		{
			int u=to[i];
			if(d2[u]>d2[v]+w[i])
			{
				d2[u]=d2[v]+w[i];
				from2[u]=(from2[v])?from2[v]:u;
				q.push(make_pair(-d2[u],u));
			}
		}
	}
}
signed main()
{
	t=read();
	while(t--)
	{ 
		tot=0;
		memset(nxt,0,sizeof(nxt));
		memset(to,0,sizeof(to));
		memset(first,0,sizeof(first));
		memset(w,0,sizeof(w));
		memset(e,0,sizeof(e));
		memset(from1,0,sizeof(from1));
		memset(from2,0,sizeof(from2));
		memset(vis,0,sizeof(vis));
		scanf("%lld%lld%lld",&n,&m,&q1);
		for(int i=1;i<=m;i++)
		{
			e[i].x=read();
			e[i].y=read();
			e[i].z=read();
			add(e[i].x,e[i].y,e[i].z);
		}
		for(int i=1;i<=q1;i++)
		{
			a[i]=read();
			ans[a[i]]=INF;
			add(n+1,a[i],0);
		}
		dj1(n+1);
		tot=0;
		memset(nxt,0,sizeof(nxt));
		memset(to,0,sizeof(to));
		memset(first,0,sizeof(first));
		memset(w,0,sizeof(w));
		for(int i=1;i<=q1;i++)
			add(n+1,a[i],0);
		for(int i=1;i<=m;i++)
			add(e[i].y,e[i].x,e[i].z);
		dj2(n+1);
		//for(int i=1;i<=n;i++)
		//	printf("%lld %lld\n",d1[i],d2[i]);
		anss=INF;
		for(int i=1;i<=m;i++)
			if(from1[e[i].x]!=from2[e[i].y])
				ans[from2[e[i].y]]=min(ans[from2[e[i].y]],d1[e[i].x]+d2[e[i].y]+e[i].z);
		anss=INF;
		for(int i=1;i<=q1;i++)
			anss=min(anss,ans[a[i]]);
		printf("%lld\n",anss); 
	}
	return 0;
}