进行实验前,请阅读Writeup
实验目录下的文件有:
daniel@u22:~/csapp/labs/datalab-handout$ tree
.
├── bits.c # 需要实现的文件,且只需要实现这个文件
├── bits.h
├── btest # 测试文件:每次编辑bits.c后都要make再运行它进行功能测试
├── btest.c
├── btest.h
├── decl.c
├── dlc # data lab checker,检查是否满足限制要求
├── Driverhdrs.pm
├── Driverlib.pm
├── driver.pl
├── fshow # 查看浮点数的二进制表示
├── fshow.c
├── ishow # 查看整数的二进制表示
├── ishow.c
├── Makefile
├── README
└── tests.c
0 directories, 17 files
bitXor
使用 ~ 和 & 实现异或运算
列出异或运算的真值表:
| a | b | a ^ b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
得出使用与或非表达的逻辑表达式为(类似于析取范式的形式):
Y = (~a & b ) | (a & ~b)
由于题目限制,我们进一步使用DeMorgen律消去“或”联结词:
Y = ~( ~ ( ~a & b) & ~ (a & ~b) )
所以本题的答案为:
int bitXor(int x, int y) {
return ~(~(~x & y) & ~(x & ~y));
}
$ ./dlc bits.c # 检查是否满足限制要求
$ make
$ ./btest -f bitXor # 测试功能是否正确
Score Rating Errors Function
1 1 0 bitXor
Total points: 1/1 # 通过了测试
tmin
求补码表示的最小负数,当然是 0x8000_0000
int tmin(void) {
return 1<<31;
}
isTmax
使用 ! ~ & ^ | + 这些运算符实现判断一个数是否为INT_MAX。若是返回1,否则返回0
由于 INT_MAX = 0X7fff_ffff,将其加1后得到 0x8000_0000,然后取反得到 0x7fff_ffff
所以一种native的想法是将其加一取反后再与原数据做异或,如果得到0,就说明它是INT_MAX
但测试结果表明这是错误的,因为 0xffff_ffff 经过上述运算后也能得到0,如何绕开这个bug呢?我们可以再加上一个限制条件:加一后结果不为0
也就是下面的代码所示:
int isTmax(int x) {
int a = x + 1;
int b = ~a;
return (!(b ^ x) & a); //加一取反异或==0 && 加一!=0
}
但是上面的代码还是不能通过测试,问题很明显:当我们用“位与”代替了“逻辑与”,试想输入INT_MAX时,!(b ^ a) = 0x0000_0001 的结果为1,而 a = 0x1000_0000,二者相与还是0,结果错误
如何改进呢——使用DeMorgen律,把“位与”换成“位或”,因为“位或”和“逻辑或”的语义更加相近。于是我们得到了下面的正确答案:
int isTmax(int x) {
int a = x + 1;
int b = ~a;
return !((b ^ x) | !a);
}
检查编译测试一条龙:
$ ./dlc -e bits.c && make && ./btest -f isTmax
allOddBits
检测是否所有奇数位都为1
思路很简单,让x与 0xaaaa_aaaa 进行“位与”运算,则当且仅当“位与”的结果还是 0xaaaa_aaaa 时,满足检测条件:
int allOddBits(int x) {
int mask, a;
mask = 0xaa;
mask <<= 8, mask |= 0xaa;
mask <<= 8, mask |= 0xaa;
mask <<= 8, mask |= 0xaa;
a = x & mask;
return !(a ^ mask);
}
注意,在题目不允许使用 == 进行判等的情况下,要用异或
negate
求相反数。牢记求补规则:所有位取反,末尾加1
int negate(int x) {
return (~x) + 1;
}
isAsciiDigit
判断x是否是一个ascii数字,即是否在0x30到0x39之间
判定过程分为2步:
首先判断x的最低字节的高4位是否=3:
- 让x位与
0xffff_fff0,判定其结果是否为0x0000_0030(用异或判等)
然后判断x的最低字节的低4位是否在0和9之间,这相当于在实现一个“比较器”,判断低4位是否<9。我们需要分析一下大于9的数字的位模式:
| 数值 | 二进制 |
|---|---|
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
我们将低四位的二进制编码表示为 b 3 b 2 b 1 b 0 b_3b_2b_1b_0 b3b2b1b0,则根据位模式,判定一个数字y是否大于9的逻辑表达式为:
Y = b 3 & ( b 2 ∣ b 1 ) Y = b_3 \&(b_2 | b_1) Y=b3&(b2∣b1)
受限于允许使用的操作符,我们可以通过如下两步进行判断:
- 让x位与
0xffff_fffa,若得到的结果是0x0000_003a,则说明 b 3 = = 1 & & b 1 = = 1 b_3 == 1 \&\& b_1 == 1 b3==1&&b1==1,这是x>0x39的一个充分条件 - 让x位与
0xffff_fffc,若得到的结果是0x0000_003c,则说明 b 3 = = 1 & & b 2 = = 1 b_3 == 1 \&\& b_2 == 1 b3==1&&b2==1,这又是x>0x39的一个充分条件
上面两个充分条件“或”在一起,构成了x>0x39的充要条件
int isAsciiDigit(int x) {
int x1, x2, x3, mask;
x1 = x2 = x3 = x;
mask = 1 << 31, mask >>= 27; //mask = 0xffff_fff0
x1 &= mask;
x1 ^= 0x30;
mask |= 0x0a; //mask = 0xffff_fffa
x2 &= mask;
x2 ^= 0x3a; //if x==0xa or x == 0xb, then x2 == 0
mask ^= 0x06; //mask = 0xffff_fffc
x3 &= mask;
x3 ^= 0x3c; //if 0xc <= x <= 0xf, then x3 == 0
return !(x1 | !x2 | !x3);
}
conditional
要求使用位运算实现 x ? y : z
很自然的想法就是:
- 当x=0,需要返回z,那么就让z位与
0xffff_ffff;否则,让z位与0x0000_0000,消灭掉它 - 当x=1,需要返回y,那么就让y位与
0xffff_ffff;否则,让y位与0x0000_0000,消灭掉它
把上面的两个表达式“位或”在一起,就能实现选择的目的了:
int conditional(int x, int y, int z) {
return (z & (((!x) << 31) >> 31)) | (y & (((!(!x))<<31) >> 31));
}
isLessOrEqual
使用位运算实现判断 <= 的逻辑
类似于x86的 jle 条件转移指令,我们可以采用先做差,再判断差值的符号位进行判断。同时要注意将 x == y 的情况单独考虑,并考虑溢出
首先,当 x == y 时,很容易得到判断条件为:
c1 = !(x ^ y)
/*
if (x == y) c1 = 1;
else c1 = 0
*/
如果x != y,我们通过做差的方式进行判断 difference_sign = (y - x) & 0x8000_0000
- 如果 x 与 y 的符号位相同,则减法过程不会产生溢出,判断结果Y与
!difference_sign保持一致 - 如果 x 与 y 的符号位不同,则不论减法过程溢出与否,我们只需要简单地考虑x的符号位即可:如果x是正数,那么y一定是负数,结果为true,and vice versa。所以判断结果Y与x的符号位保持一致即可
列出真值表如下:
| is_same_sign | difference_sign | x _sign | y_sign | Y |
|---|---|---|---|---|
| 1 | 0 | x | x | 1 |
| 1 | 1 | x | x | 0 |
| 0 | x | 1 | 0 | 1 |
| 0 | x | 0 | 1 | 0 |
于是我们得到Y的逻辑表达式:
Y = i s _ s a m e _ s i g n & & ! d i f f e r e n c e _ s i g n ∣ ∣ ! i s _ s a m e _ s i g n & & x _ s i g n Y = is\_same\_sign \&\& !difference\_sign || !is\_same\_sign \&\& x\_sign Y=is_same_sign&&!difference_sign∣∣!is_same_sign&&x_sign
将上面的逻辑用位运算表达即可:
int isLessOrEqual(int x, int y) {
int nx, is_same_sign, difference_sign, x_sign, mask, c1, c2, c3;
nx = (~x) + 1;
mask = (1 << 31); // mask = 0x8000_0000
difference_sign = ((y + nx) & mask); // 0x0000_0000 or 0x8000_0000
x_sign = (x & mask); // 0x0000_0000 or 0x8000_0000
is_same_sign = !((x ^ y) & mask); // 1 or 0
c1 = !(x ^ y); // 1 or 0
c2 = (is_same_sign) & (!difference_sign); //x and y has the same sign, c2 will be 1 or 0
c3 = (((!is_same_sign) << 31) & x_sign); // x and y has different sign, c3 will b 0x8000_0000 or 0x0000_0000
return !!(c1 | c2 | c3); //cast to boolean value: 1 or 0
}
logicalNeg
题目要求:使用位运算实现 ! 的逻辑
首先考虑我们如何在不借助 ! 运算符的情况下将任意的非0值映射到1,而将0值还映射到0,也就是实现一个 cast int to boolean 的功能:
我的想法是:若数字x非0,如果能够则将其任意位置的1“扩展”到所有位,再与1做“位与”运算,就能得到1;而0直接与1做“位与”运算就能得到0
那么如何实现这个“扩展”操作呢?——我们能想到,“符号位”是一个不错的“任意位置”,因为在算术右移的过程中,最高位填充1,将一个负数右移31次,就能得到“全1”。至于正数,取反即可
现在我们得到了 cast int to boolean 的功能,这与题目要求的逻辑是反的,所以为了把1变0,把0变1,我们需要将结果与1做异或。于是得到下面的代码:
int logicalNeg(int x) {
int nx;
nx = (~x) + 1;
return (((x >> 31) & 1) | ((nx >> 31) & 1)) ^ 1;
}
howManyBits
求使用二进制补码表示一个数字所需要的最小比特数
这道题我没做出来,参考了这里的视频讲解,思路非常精妙。这道题是我觉得最难的一道题:
int howManyBits(int x) {
int mask, bit_16, bit_8, bit_4, bit_2, bit_1, bit_0;
mask = x >> 31;
x = (~mask & x) | (mask & ~x); //正数不变,负数取反
bit_16 = (!!(x >> 16)) << 4;
x >>= bit_16;
bit_8 = (!!(x >> 8)) << 3;
x >>= bit_8;
bit_4 = (!!(x >> 4)) << 2;
x >>= bit_4;
bit_2 = (!!(x >> 2)) << 1;
x >>= bit_2;
bit_1 = (!!(x >> 1));
x >>= bit_1;
bit_0 = x;
return (!x) | (bit_16 + bit_8 + bit_4 + bit_2 + bit_1 + bit_0 + 1);
}
floatScale2
使用位运算求浮点数 f 的2倍,当参数位NaN时,直接返回参数
首先将阶码部分取出:
exp = uf & 0x7f800000;
- 当阶码为255,说明这是NaN或无穷大,直接返回参数即可
- 否则,当阶码不为0,说明这是一个规格化数,我们只需将阶码+1,然后将其放回原位置
- 否则,阶码为0,说明这是一个非规格化数,则只需将尾数左移1位就能实现乘以2,但是要注意处理符号位
unsigned floatScale2(unsigned uf) {
int exp;
exp = uf & 0x7f800000;
if (exp == 0x7f800000) { // Not a Number
return uf;
} else if (exp != 0){ // Normalized value
exp = exp >> 23;
exp += 1;
exp = exp << 23;
uf = (uf & 0x807fffff) | exp;
return uf;
} else { //DeNormalized value
int sign = uf & 0x80000000;
return (uf << 1) | sign;
}
}
floatFloat2Int
使用位运算实现“将一个浮点数转化为整数”,对于超过int表示范围的数字,返回 0x80000000u
首先将阶码部分和符号位取出:
exp = uf & 0x7f800000;
sign = uf & 0x80000000;
- 若阶码为255,说明这是NaN或无穷大,直接返回
0x80000000u - 否则,若阶码为0,说明这是一个非规格化的值,根据其定义,这一定是小于1的数(在0附近),取整必为0,直接返回0即可
- 否则,阶码在1~254之间,这是一个规格化的值:
- 首先取出尾数frac,并将阶码转化到真正的指数值
- 若指数值 < 0,说明这个值在(-1, 1),返回0即可
- 否则,指数值 > 0,这个值比1大:
- 如果指数值 < = 23,小数点右移的次数不超过23,需要舍弃掉frac剩下的部分,则我们需要将frac右移
23 - exp位 - 否则,如果指数值 <= 31,小数点右移的次数超过了23,需要在frac右边补0,则我们需要将frac左移
exp - 23位 - 否则,结果超出了int的表示范围(高位溢出),返回
0x80000000u
- 如果指数值 < = 23,小数点右移的次数不超过23,需要舍弃掉frac剩下的部分,则我们需要将frac右移
- 返回之前注意符号位
int floatFloat2Int(unsigned uf) {
int exp, frac, sign, ret;
exp = uf & 0x7f800000;
sign = uf & 0x80000000;
if (exp == 0x7f800000) { //NaN and infinity
return 0x80000000u;
} else if (exp == 0) { //0
return 0;
} else {
exp >>= 23;
exp -= 127;
frac = (uf & 0x007fffff) | 0x00800000;
if (exp >= 0) {
if (exp <= 23) {
ret = frac >> (23 - exp);
} else if (exp <=31){
ret = frac << (exp - 23);
} else {
return 0x80000000u;
}
return sign ? (~ret) + 1 : ret;
} else {
return 0;
}
}
}
floatPower2
通过位运算实现 2.0^x 的功能,其中x是一个整数。如果结果上溢,返回 +INF;如果结果下溢,返回0
首先考虑 x >= 0,这时很简单,因为尾数一定是0:
- 如果x不超过127,则说明结果不会上溢,直接将x + 127变为阶码后,左移23位即可
- 否则,结果上溢,返回
0x7f800000
接下来考虑 x < 0,这时需要考虑规格化和非规格化的情况:
- 如果 x >= -126,这时为规格化的情况,还是将x + 127变为阶码后,左移23位即可
- 否则,这时来到了非规格化的情况,我们需要通过移动尾数中的1来实现pow功能:如果 x >= -149,说明此时还能用尾数表达结果(尾数中的1还没有被右移出去),则我们需要返回尾数右移之后的值
- 否则,产生了下溢(阶码全0,尾数中的1被右移出去了),返回0
unsigned floatPower2(int x) {
int frac;
if (x >= 0) {
if (x <= 127) {
return (x + 127) << 23;
} else {
return 0x7f800000; //+INF
}
} else {
if (x >= -126) {
return (x + 127) << 23;
} else if (x >= -149){
frac = 0x00400000;
return frac >> (-126 - x);
} else {
return 0;
}
}
}
我们的代码拿到了全部的分数:
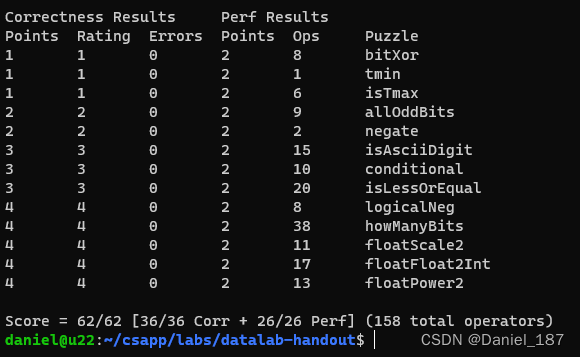





 本文详细介绍了如何使用位运算符(如异或、与、或、非等)来实现特定的计算任务,包括求补码表示的最小负数、判断是否为INT_MAX、检测所有奇数位是否为1、求相反数、判断ASCII数字、实现条件选择、比较运算以及浮点数的位操作。每个任务都给出了逻辑分析和位运算的解决方案,并提供了相应的测试验证。
本文详细介绍了如何使用位运算符(如异或、与、或、非等)来实现特定的计算任务,包括求补码表示的最小负数、判断是否为INT_MAX、检测所有奇数位是否为1、求相反数、判断ASCII数字、实现条件选择、比较运算以及浮点数的位操作。每个任务都给出了逻辑分析和位运算的解决方案,并提供了相应的测试验证。
















 5560
5560

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








