计算机中的进制 & 进制转换 & 位运算符号

进制

计算机内部是由 IC（intergrated Ciruit）这种电子部件构成， CPU 和内存也是 IC 的一种，IC的所有引脚只有直流电压 0V 或 5V两个状态，也就是说 IC 的一个引脚只能表示两个状态。现代计算机都是基于 0、1两个符号表示信息的，即现代计算机中数值的表示是二进制。

进制的定义

进制：进位计数制的简称，指针数的方法，一般用于刻画实物之间的数量关系，是人们长期实践中发现和发明的。

十进制

运算规则：逢十进一

十进制是我们日常中最熟悉的进制方法，计数符号使用 0～9 来记录数字的大小，根据数字中所处的位置不同代表的数值大小也是不同。

N 进制

逢 n 进一，即为 n 进制

进制	R值	计数符号
十进制	10	1,2,3,4,5,6,7,8,9
八进制	8	1,2,3,4,5,6,7
二进制	2	0,1
十六进制	16	0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

计算机中的进制

现代计算机都是基于 0、1 两个符号表示信息的，即现代计算机中数值的表示是二进制。

为什么计算机采用二进制系统（二进制和十进制对比）

• 采用二进制系统更经济

  二进制的 33 位表示最大可以表示 10 的 10 次方量级的数

  一个 33 位的二进制数需要的状态是 2*33=66中

  一个10位的十进制数需要的状态是10*10=100种

  由此可见二进制所需要的状态数更少

• 物理实现方面：要找到两个稳定状态是相对容易的，系统的稳定性可靠性更高

  两个状态：电压高低，电流有无等

  十个稳定状态：很难找且很难维护可靠性和稳定性

• 算数运算规则二进制运算规则简单，可简化运算器等物理器件的设计

  二进制只需要计算 0、1

  十进制需要 0～9 运算 99 加法

• 逻辑运算真假都可以用 0 和 1 表示，可使电子机械装置的计算通用性更强

进制转换

进制转换算法

通常我们在数字后面加上不同的字母来表示不同进位制，B（Binary）表示二进制，O（Octal）表示八进制，D（D ecimal）或不加表示十进制，H（Hexadecimal）表示十六进制。

(二、八、十六进制) 转换为 十进制

• 二进制转换为十进制

  二进制数从低位到高位**（即从右到左）**计算，第 0 位的权值是 2 的0次方，第一位的权值是2的1次方，第2位的权值是2^2一次递增下去，把最后的结果相加后的值就是十进制的值。

  # eg: 将二进制数（101011）B 转换为十进制的步骤：
  1. 第0位 1 x 2^0 = 1；
  
  2. 第1位 1 x 2^1 = 2；
  
  3. 第2位 0 x 2^2 = 0；
  
  4. 第3位 1 x 2^3 = 8；
  
  5. 第4位 0 x 2^4 = 0；
  
  6. 第5位 1 x 2^5 = 32；
  
  7. 读数，把结果值相加，1+2+0+8+0+32=43，即(101011)B=(43)D。
  

• 八进制转换为十进制

  八进制数从低位到高位（从右往左）计算，第 0 位的权值是 8 的 0 次方，第一位是8的一次方，第二位的权值是8的2次方，依次递增下去，把最后的结果相加后的值就是十进制的值。

  # eg 将八进制 （52）O 转换为十进制：
  1. 第0位 3 x 8^0 = 3；
  
  2. 第1位 5 x 8^1 = 40；
  
  3. 读数，把结果值相加，3+40=43，即(53)O=(43)D。
  

• 十六进制转换为十进制

  十六进制数从低位到高位（从右往左）计算，第 0 位的权值是 16 的 0 次方，第一位是16的一次方，第二位的权值是16的2次方，依次递增下去，把最后的结果相加后的值就是十进制的值。

  # eg: 将十六进制的（2B）H 转换为十进制的步骤：
  1. 第0位 B x 16^0 = 11；
  
  2. 第1位 2 x 16^1 = 32；
  
  3. 读数，把结果值相加，11+32=43，即(2B)H=(43)D。
  

十进制 => （二、八、十六进制）

• 十进制转换为二进制

  除2取余法，每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数上有为上一个位权上的数，重复这个步骤直到商为0，最后读书的时候从最后一个余数读起一直到最前面的一个余数

  # 将十进制的(43)D转换为二进制的步骤如下：
  1. 将商43除以2，商21余数为1；
  
  2. 将商21除以2，商10余数为1；
  
  3. 将商10除以2，商5余数为0；
  
  4. 将商5除以2，商2余数为1；
  
  5. 将商2除以2，商1余数为0； 
  
  6. 将商1除以2，商0余数为1； 
  
  7. 读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，101011，即(43)D=(101011)B。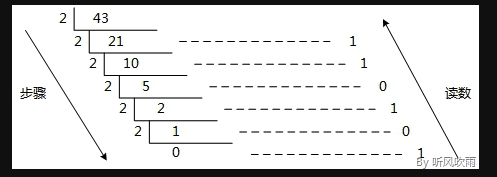
  

  

• 十进制转换为八进制

  除8取余法，即每次将整数部分除以8，余数为该位权上的数，而商继续除以8，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数起，一直到最前面的一个余数。

  # eg: 将十进制的(796)D转换为八进制的步骤如下：
  
  1. 将商796除以8，商99余数为4；
  
  2. 将商99除以8，商12余数为3；
  
  3. 将商12除以8，商1余数为4；
  
  4. 将商1除以8，商0余数为1；
  
  5. 读数，因为最后一位是经过多次除以8才得到的，因此它是最高位，读数字从最后的余数向前读，1434，即(796)D=(1434)O。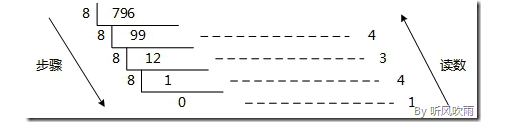
  

  

• 十进制转换为十六进制

  除16取余法，即每次将整数部分除以16，余数为该位权上的数，而商继续除以16，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数起，一直到最前面的一个余数。

  # eg:将十进制的(796)D转换为十六进制的步骤如下：
  
  1. 将商796除以16，商49余数为12，对应十六进制的C；
  
  2. 将商49除以16，商3余数为1；
  
  3. 将商3除以16，商0余数为3；
  
  4. 读数，因为最后一位是经过多次除以16才得到的，因此它是最高位，读数字从最后的余数向前读，31C，即(796)D=(31C)H。
  

  

二进制转换为八、十六进制

• 二进制转换为八进制

  取三合一法，即从二进制的小数点为分界点，向左（向右）每三位取成一位，接着将这三位二进制按权相加，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的八进制数。如果向左（向右）取三位后，取到最高（最低）位时候，如果无法凑足三位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足三位

  # eg 将二进制的(11010111.0100111)B转换为八进制的步骤如下：
  
  1. 小数点前111 = 7；
  
  2. 010 = 2；
  
  3. 11补全为011，011 = 3；
  
  4. 小数点后010 = 2；
  
  5. 011 = 3；
  
  6. 1补全为100，100 = 4；
  
  7. 读数，读数从高位到低位，即(11010111.0100111)B=(327.234)O。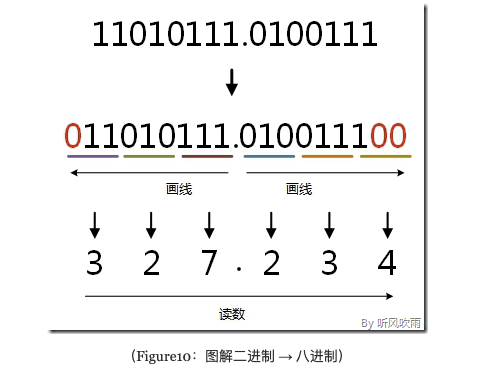
  

  

  二进制与八进制编码对应表：

  二进制	八进制
  000	0
  001	1
  010	2
  011	3
  100	4
  101	5
  110	6
  111	7

• 八进制转换为二进制

  取一分三法，即将一位八进制数分解成三位二进制数，用三位二进制按权相加去凑这位八进制数，小数点位置照旧。

  # 将八进制的(327)O转换为二进制的步骤如下：
  
  1. 3 = 011；
  
  2. 2 = 010；
  
  3. 7 = 111；
  
  4. 读数，读数从高位到低位，011010111，即(327)O=(11010111)B。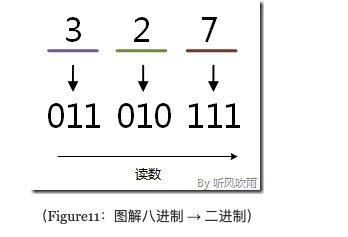
  

  

• 二进制转换为十六进制

  取四合一法，即从二进制的小数点为分界点，向左（向右）每四位取成一位，接着将这四位二进制按权相加，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的十六进制数。如果向左（向右）取四位后，取到最高（最低）位时候，如果无法凑足四位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足四位。

  # eg 将二进制的(11010111)B转换为十六进制的步骤如下：
  
  1. 0111 = 7；
  
  2. 1101 = D；
  
  3. 读数，读数从高位到低位，即(11010111)B=(D7)H。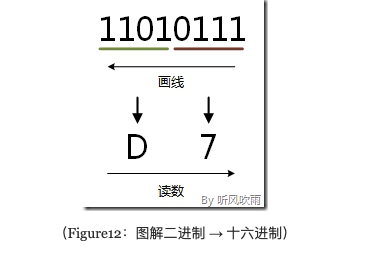
  

  

八进制转换为十六进制

• 八进制转十六进制

  将八进制转换为二进制，然后再将二进制转换为十六进制，小数点位置不变。

  # eg 将八进制的(327)O转换为十六进制的步骤如下：
  
  1. 3 = 011；
  
  2. 2 = 010；
  
  3. 7 = 111；
  
  4. 0111 = 7；
  
  5. 1101 = D；
  
  6. 读数，读数从高位到低位，D7，即(327)O=(D7)H。
  

  

• 十六进制转八进制

  将十六进制转换为二进制，然后再将二进制转换为八进制，小数点位置不变。

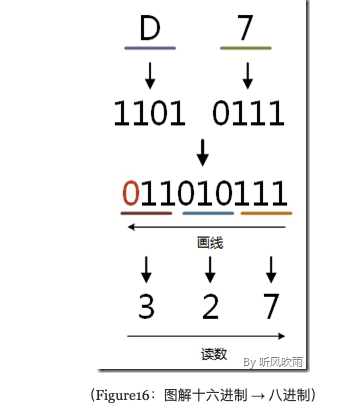
  将十六进制的(D7)H转换为八进制的步骤如下：
  
  1. 7 = 0111；
  
  2. D = 1101；
  
  3. 0111 = 7；
  
  4. 010 = 2；
  
  5. 011 = 3；
  
  6. 读数，读数从高位到低位，327，即(D7)H=(327)O。
  

总结：

二进制、八进制、十六进制转十进制

• 从低位到高位（即从右往左）计算，第0位的权值是2的0次方，第1位的权值是2的1次方，第2位的权值是2的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了

十进制转换为二进制、八进制、十六进制

• 除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数（十进制转换为二进制）
• 除8取余法，即每次将整数部分除以8，余数为该位权上的数，而商继续除以8，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数起，一直到最前面的一个余数（十进制转换为八进制）
• 除16取余法，即每次将整数部分除以16，余数为该位权上的数，而商继续除以16，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数起，一直到最前面的一个余数（十进制转换为十六进制）

八进制 → 十六进制

方法：将八进制转换为二进制，然后再将二进制转换为十六进制，小数点位置不变。

十六进制 → 八进制

方法：将十六进制转换为二进制，然后再将二进制转换为八进制，小数点位置不变。

位运算

计算机中的数字都是二进制形式表示的（0、1），在 python 中给数字钱前面加上前缀 ‘0b’ 表示是二进制数字，如下所示，左边是二进制右边是值，在 python 中我们可以通过 bin(num) 、oct(num)、hex(num)查看数字在二进制、八进制、十六进制 在python 中的表示形式。

python 中的位运算符

按位运算符是吧数字看作二进制来进行计算的

a = 0011 1100

b = 0000 1101

-----------------

a&b = 0000 1100

a|b = 0011 1101

a^b = 0011 0001

~a  = 1100 0011

运算符	描述	实例
&	按位与运算符：参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0	(a & b) 输出结果 12 ，二进制解释： 0000 1100
|	按位或运算符：只要对应的二个二进位有一个为1时，结果位就为1。	(a | b) 输出结果 61 ，二进制解释： 0011 1101
^	按位异或运算符：当两对应的二进位相异时，结果为1	(a ^ b) 输出结果 49 ，二进制解释： 0011 0001
~	按位取反运算符：对数据的每个二进制位取反,即把1变为0,把0变为1 。~x 类似于 -x-1	(~a ) 输出结果 -61 ，二进制解释： 1100 0011，在一个有符号二进制数的补码形式。
<<	左移动运算符：运算数的各二进位全部左移若干位，由 << 右边的数字指定了移动的位数，高位丢弃，低位补0。	a << 2 输出结果 240 ，二进制解释： 1111 0000
>>	右移动运算符：把">>"左边的运算数的各二进位全部右移若干位，>> 右边的数字指定了移动的位数	a >> 2 输出结果 15 ，二进制解释： 0000 1111

参考