动态规划之【 LCS & DP 】_lcs dp-优快云博客

博客介绍了最长公共子序列（LCS）原理及转移方程，还阐述了最长公共子串（DP）连续的原理和转移方程，最后给出了相关代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最长公共子序列(LCS)原理
转移方程

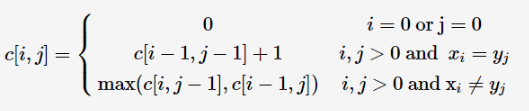
最长公共子串（DP）连续的原理
转移方程

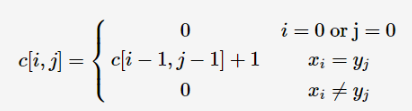
代码

#include<iostream>
#include<string.h>
using namespace std;
int dp(string str1,string str2);
int lcs(string str1,string str2);
int main()
{
	string str1="bdcaba";
	string str2="abcbdab";

	cout<<lcs(str1,str2);//bcba
	cout<<dp(str1,str2);//abcd
}
//最长公共子序列
int lcs(string str1,string str2)
{
	int len1 = str1.length();  
    int len2 = str2.length();  
    int c[100][100];
    for (int i = 0; i <= len1; i++) 
	{  
        for( int j = 0; j <= len2; j++) 
		{  
            if(i == 0 || j == 0) 
			{  
                c[i][j] = 0;  
            } 
			else if (str1[i-1] == str2[j-1])
			{
                c[i][j] = c[i-1][j-1] + 1;  
            } 
			else 
			{  
                c[i][j] = max(c[i - 1][j], c[i][j - 1]);  
            }  
        }  
    }  
    return c[len1][len2];  
}
//最长公共子串长度
int dp(string str1,string str2)
{
	int len1 = str1.length();  
    int len2 = str2.length();  
    int result = 0;     //记录最长公共子串长度  
    int c[100][100];
    for (int i = 0; i <= len1; i++) 
	{  
        for( int j = 0; j <= len2; j++) 
		{  
            if(i == 0 || j == 0) {  
                c[i][j] = 0;  
            } 
			else if (str1[i-1] == str2[j-1])
			{  
                c[i][j] = c[i-1][j-1] + 1;  
                result = max(c[i][j], result);  
            }
			else {  
                c[i][j] = 0;  
            }  
        }  
    }  
    return result;  
}