Part1_编写自己的解释器

如果你不知道编译器是如何工作的，那么你就不知道计算机是如何工作的。如果你不能确定你是否完全知道编译器是如何工作的，那么你就是不知道它是如何工作的。

如上所述。仔细思考。无论你是软件开发的新手还是经验丰富的老鸟，有一个规则都适用：如果你不知道编译器和解释器是如何工作的，那你就是不知道计算机是如何工作的。就这么简单。

那么，你知道编译器和解释器是怎么工作的吗？我的意思是，你确定你完全知道它们的工作原理吗？如果不确定。或者如果你在不确定的同时又对它非常迷茫。不要担心。如果你可以坚持跟着本系列教程走下去，并在最后成功构建了一个编译器和解释器的话，到时候你就知道它们是如何工作的了。你也会成为一个自信的人。至少我是这样希望的。

为什么你要去学习编译器和解释器呢？我会给你三个理由：

1. 要编写一个解释器或者编译器，你不得不同时运用多种专业技能。编写一个解释器或编译器，能够帮助你提升这些专业技能，让你成为一个更棒的软件开发者。而且，你学到的这些技能对你开发任何其他的应用软件都是有帮助的，而不仅仅是解释器或编译器。
2. 你真的很想去知道计算机是如何工作的。编译器和解释器常常被看作是很神秘的。你不应该仅仅止步于被这种神秘满足而踏步不前。你想要解开它们的神秘面纱，理解它们如何工作，最终掌控它们。
3. 你想去构建属于自己的编程语言或者特定领域的语言。如果是的话，你需要去构建一个解释器或者编译器。近年来，构建新编程语言的浪潮又再度涌现。几乎每天都有新的编程语言出现：Elixir、Go、Rust…

好吧，但是解释器和编译器到底是什么呢？

解释器或编译器的目标就是将用高等语言编写的源程序翻译为其它形式的语言。相当模糊，是吧？请多包涵，在系列的后面你将会知道源程序到底被翻译成了什么东西。

这一刻，你可能想知道解释器和编译器之间的差别是什么？为了达成本系列的目的，让我们来约定：如果一个翻译器能够将源代码翻译为机器语言，那我们称之为编译器。如果一个翻译器能够直接处理并运行源代码，而不需要将其转换为机器语言，那我们称之为解释器。如下图所示：

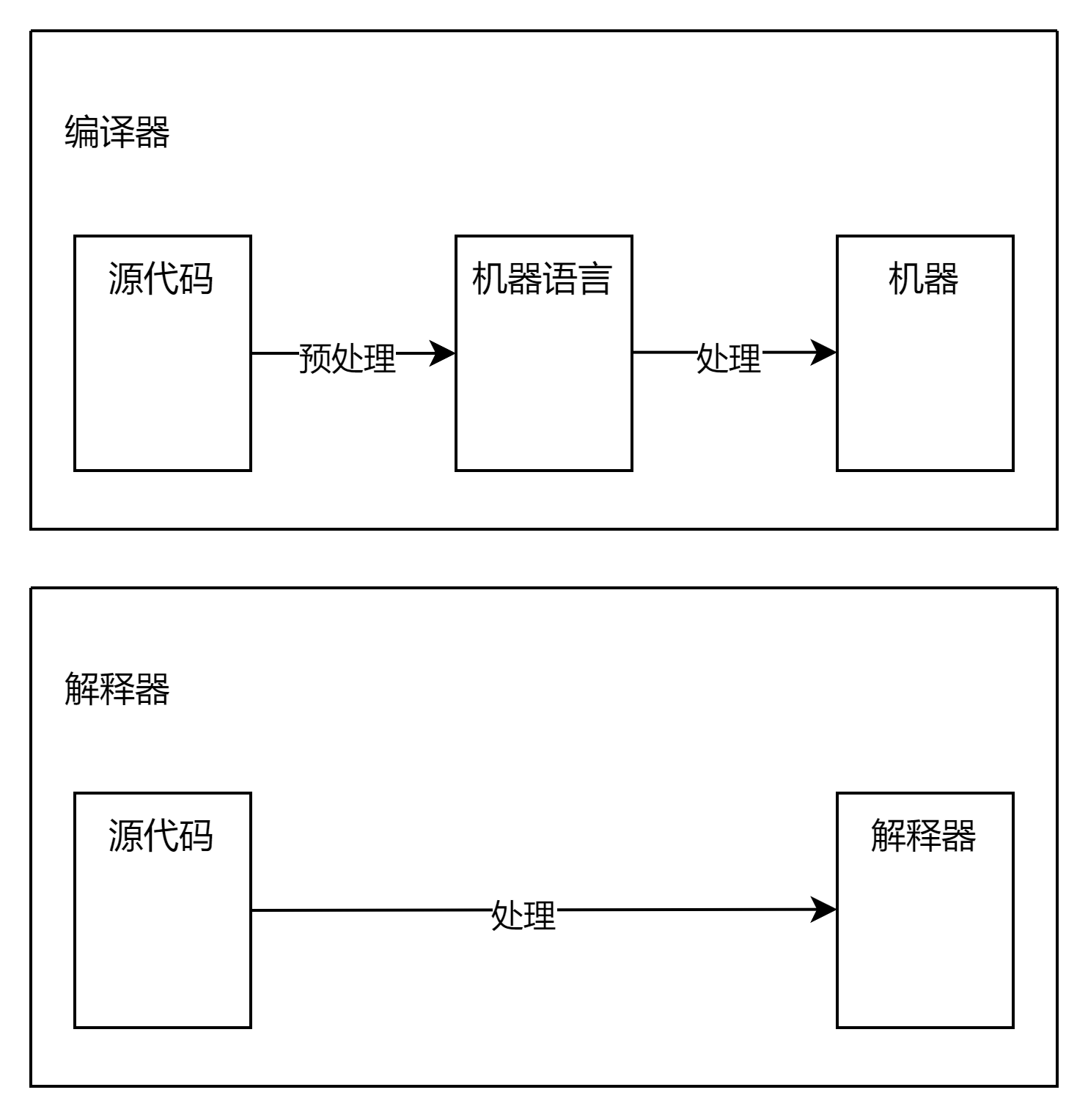
我希望现在你是真的想去学习构建一个解释器和一个编译器。关于这个基于编译器的系列，你能期待些什么呢？

答案在这里：你和我将会一起去构建一个简单的基于Pascal语言子集的解释器。在这个系列的最后，你将会拥有一个可以正常工作的Pascal解释器，以及一个源代码级别的调试器（类似于Python的pdb）。

你可能会问，为什么是Pascal？因为一件事：它是一门真正的编程语言，拥有许多重要的语言结构。而且在一些比较老，但是很有用的计算机类书籍里的例子都用Pascal语言来编写。（我明白，这并不是选择一门语言来构建解释器的特别有说服力的理由，但我认为，换换口味，学习一门非主流语言会很好。）

下面是一个使用Pascal语言编写的阶乘函数，随着系列的学习，这段代码能够放在你自己编写的解释器里运行，并且还能够互动式的使用自己编写的调试器进行调试：

program factorial;

function factorial(n: integer): longint;
begin
	if n = 0 then
		factorial := 1
	else
		factorial := n * factorial(n - 1)
end;

var
	n: integer;
	
begin
	for n := 0 to 16 do
		writeln(n, '! = ', factorial(n));
end.

Pascal解释器的实现语言将会使用Python，但是你可以使用任何你想用的语言，这是因为原理是不依赖于具体语言的。好的，那我们开始吧！准备，就绪，开始！

你对解释器的第一次学习将会通过编写一个数学表达式的解释器，就是一个计算器。今天的目标非常简单：让你的计算器能够处理两个简单数字的加法，如：3+5。下面就是计算器的代码，不好意思，是解释器的代码：

"""
EOF(end-of-file)符号用于表示在词法分析中没有更多的输入
"""
INTEGER, PLUS, EOF = 'INTEGER', 'PLUS', 'EOF'

class Token:

    def __init__(
            self,
            type: str,
            value: int | str | None
    ):
        """
        :param type: 符号类型：INTEGER（整数）、PLUS（加号）、EOF
        :param value: 0-9 | '+' | None
        """
        self.type: str = type
        self.value: int | str | None = value

    def __str__(self) -> str:
        """
        Token实例的字符串表示。

        例子：
            Token(INTEGER, 3)
            Token(PLUS, '+')
        :return:
        """

        return 'Token({type}, {value})'.format(
            type=self.type,
            value=repr(self.value)
        )

    def __repr__(self) -> str: return self.__str__()

class Interpreter:

    def __init__(self, text: str):
        # 客户端的字符串输入："3+5"
        self.text: str = text
        # self.pos是self.text中字符的索引
        self.pos: int = 0
        # 当前符号实例
        self.current_token: Token | None = None

    def error(self):
        raise Exception('输入解析错误')

    def get_next_token(self) -> Token | None:
        """
        词法解析器（也被称作扫描器或者符号序列化器）
        这个方法负责将输入的文本解析为一个个符号实例。每调用一次，解析一个符号实例。
        :return 符号实例
        """
        text: str = self.text

        # self.pos是否已经经过了self.text的最后一个字符所在的索引？
        # 如果是，返回EOF符号实例，因为已经没有更多的输入用于解析符号实例了。
        if self.pos > len(self.text) - 1:
            return Token(EOF, None)

        # 获取self.pos索引的字符，基于该字符去决定实例化对应的符号实例
        current_char: str = self.text[self.pos]

        # 如果该字符是数字，将其转换为整数，创建一个整数符号实例
        # 自增self.pos，使其指向后一个字符的索引处
        # 返回整数符号实例
        if current_char.isdigit():
            self.pos += 1
            return Token(INTEGER, int(current_char))

        # 如果该字符是加号，创建一个加号符号实例
        # 自增self.pos，使其指向后一个字符的索引处
        # 返回加号符号实例
        if current_char == '+':
            self.pos += 1
            return Token(PLUS, current_char)

        self.error()

    def eat(self, token_type: str):
        """
        比较当前符号实例的符号类型和传入的符号类型是否一致：
            1. 一致：“吃掉”当前符号实例，并且将下一个符号实例赋值给self.current_token；
            2. 不一致：抛出异常；
        :param token_type: 传入的符号类型
        """
        if self.current_token.type == token_type:
            self.current_token = self.get_next_token()
        else:
            self.error()

    def expr(self) -> int:
        """
        expr -> INTEGER PLUS INTEGER
        :return: 算数表达式的计算值
        """

        # 设置当前符号实例为解析输入得到的第一个符号实例
        self.current_token = self.get_next_token()

        # 我们假设当前符号实例是单数位的整数
        left: Token = self.current_token
        self.eat(INTEGER)

        # 我们假设当前的符号实例是"+"符号实例
        op: Token = self.current_token
        self.eat(PLUS)

        # 我们假设当前符号实例是单数位的整数
        right: Token = self.current_token
        self.eat(INTEGER)
        # 经过上面的调用后，self.current_token设置为了EOF符号实例

        # 在这一刻，INTEGER PLUS INTEGER的序列已经成功被搜寻到
        # 并且方法可以直接返回两数之和，有效的解析了客户端的输入
        return left.value + right.value


def main():

    while True:
        try:
            text: str = input('calc> ')
        except EOFError:
            break
        if not text:
            continue

        interpreter: Interpreter = Interpreter(text)
        print(interpreter.expr())

if __name__ == '__main__':
    main()

保存上面的代码。在你深入探究这些代码之前，运行它并观察结果。下面是在我的笔记本上的运行结果：

calc> 3+4
7
calc > 3+5
8
calc> 3+9
12
calc >

为了让你的简单解释器在运行的时候不报错，你的输入要满足下面的约束：

• 输入中能够出现的数字只能是单数位的
• 该版本目前能够支持的运算符操作只有加法
• 输入中不能出现空白字符

为了使计算器足够简单，这些约束条件是必须的。不要担心，很快你将会使得这个计算器能够进行更复杂的操作。

好了，现在我们该去探究你的解释器是如何工作的，以及它是怎样去计算算数表达式的。

当你在命令行中键入表达式$3+5$时，你的解释器会接受到字符串类型的$"3+5"$的输入。为了能够让解释器理解如何去处理字符串$"3+5"$，第一步要将其拆分为一个一个的组件，我们称这些组件为一个一个的符号。一个符号就是一个拥有其类型和值的对象。举个例子：对于源于字符串$"3"$生成的符号来说，该符号的类型是整数，对应的值为整数$3$。

将输入字符串解析为符号的过程，我们称之为词法解析。因此，你的解释器要做的第一件事就是要把输入的符号序列转化为符号流。解释器中负责做这个工作的部分，我们称之为词法解析器。你或许也会碰到该组件的别称：扫描器或者符号序列化器。它们都表示一个东西：你的解释器或编译器中负责将字符输入转换为符号流的部分。

Interpreter类中的get_next_token方法就是你的词法解析器。每次去调用它，都会获得下一个创建的符号实例，获得的符号就源于输入到解释器中的字符。窥视深渊吧！输入的字符串被存住在变量text中，pos是text中字符的索引位置。pos初始化为0，指向字符${}^{\prime }{3}^{\prime }$。方法首先会去检查当先指向的字符是否为数字，如果是数字，自增然后返回类型为$INTEGER$，值为整数$3$的符号实例对象。

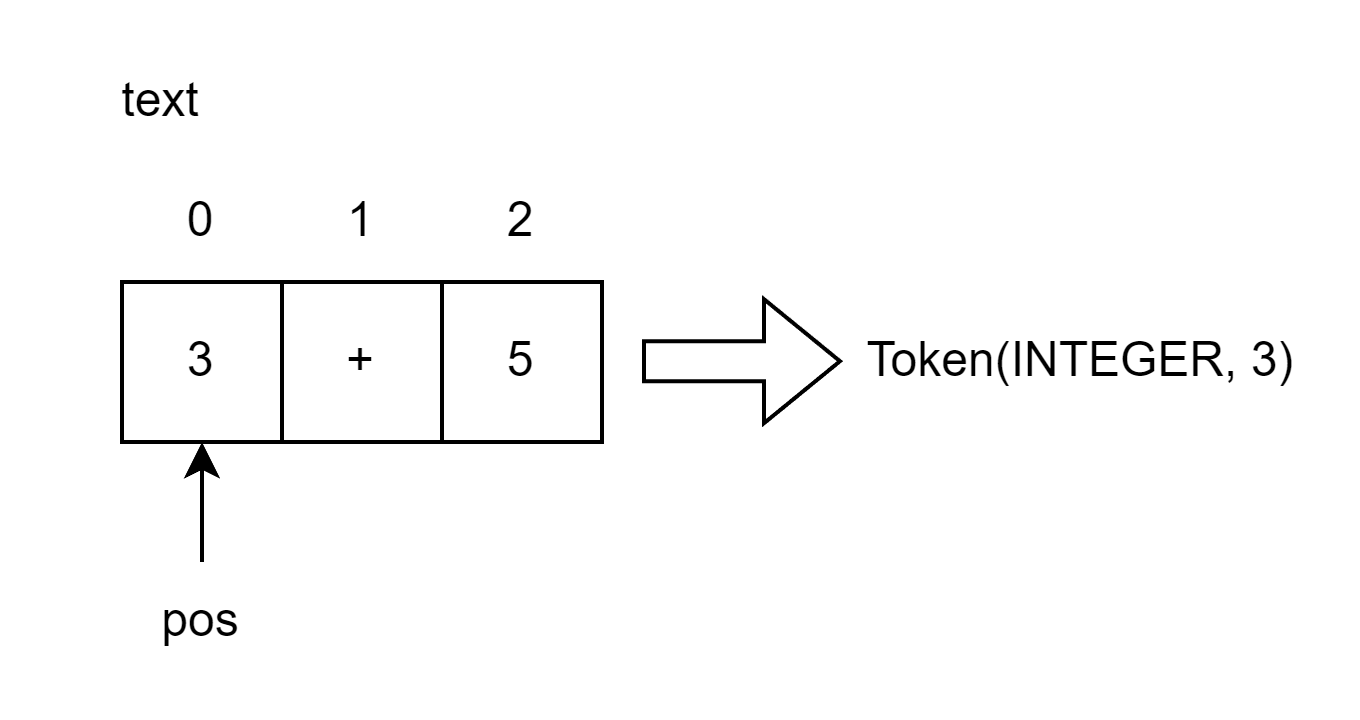
现在，pos指向了text中的${}^{\prime }{+}^{\prime }$。下一次你带用该方法的时候，首先会检查$pos$指向的字符是否为数字，明显不是，会继续判断指向的字符是否为${}^{\prime }{+}^{\prime }$。结果，pos会先自增，然后返回类型为$PLUS$，值为字符串${}^{\prime }{+}^{\prime }$的符号实例对象。

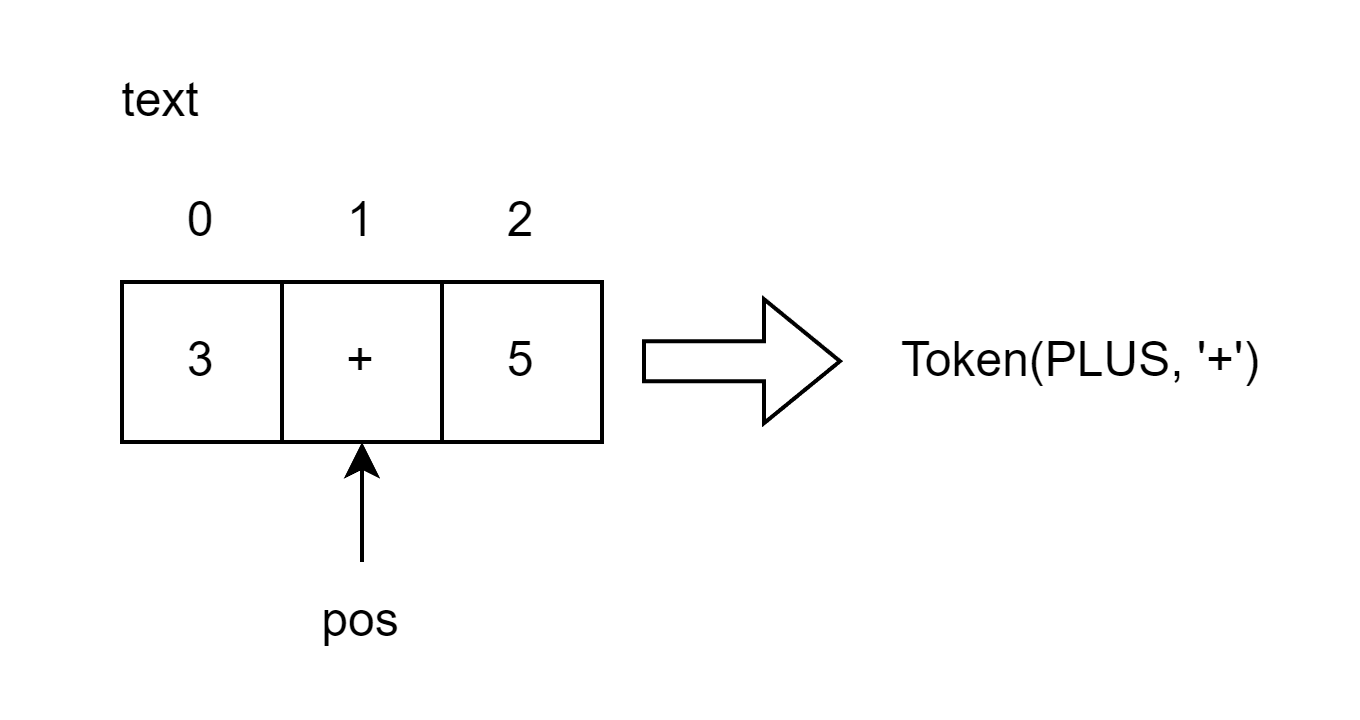
pos现在指向了字符${}^{\prime }{5}^{\prime }$。当你再次调用get_next_token方法时，发现当前指向的字符是一个数字，因此会先自增并返回类型为$INTEGER$，值为整数$5$的符号实例对象。

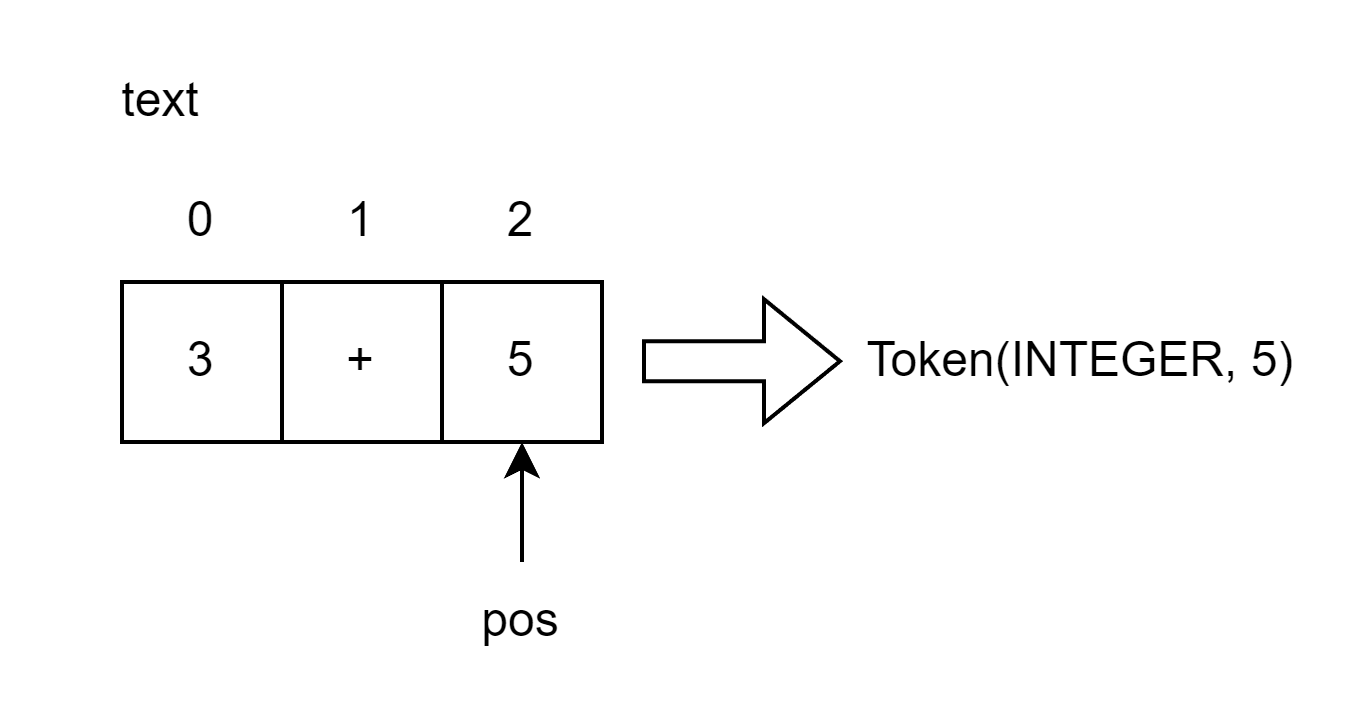
因为现在pos索引已经经过了字符串末尾，之后你每次调用get_next_token方法时，它都会返回EOF符号：

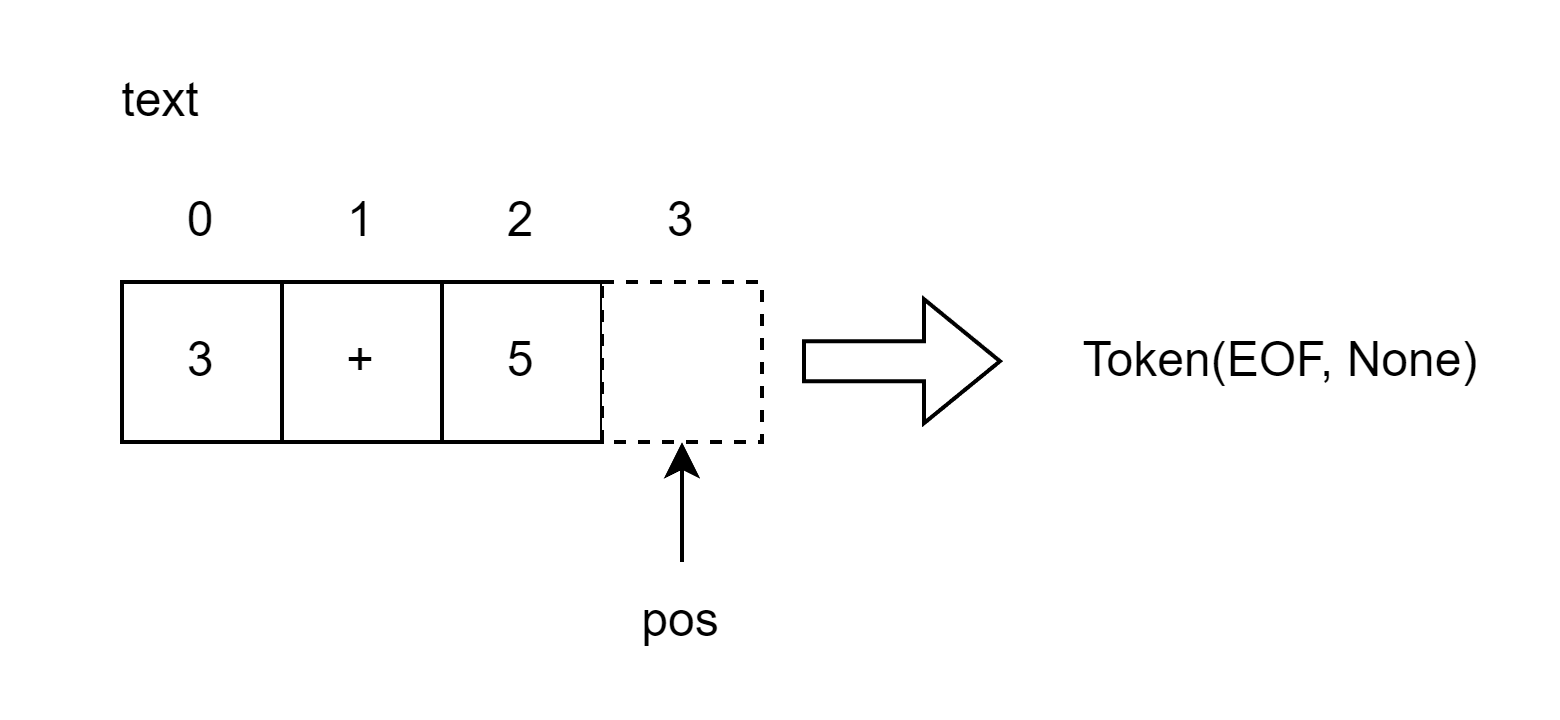
快去试一试，并且看一看你的语法解析器部分是如何工作的：

>>> interpreter = Inteperter('3+5')
>>> interpreter.get_next_token()
Token(INTEGER, 3)

>>> intepreter.get_next_token()
Token(PLUS, '+')

>>> intepreter.get_next_token()
Token(INTEGER, 5)

>>> intepreter.get_next_token()
Token(EOF, None)

因此，现在你的解释器就可以访问符号流了。接下来你的解释器就需要根据得到的符号流去解析结构。你的解释器希望从输入的符号流中解析得到的结果为：INTEGER->PLUS->INTEGER。也就是说，它尝试找到这样的一个结构：整数后面跟一个加号，加号后面跟一个整数。

expr方法使用了一个帮助方法：eat，该帮助方法负责检测传入的符号类型和当前保存的符号的符号类型是否一致。如果一致，调用get_next_token方法获取下一个符号实例，并将获取到的下一个实例赋值给current_token变量，即会将之前匹配的符号消耗掉，让current_token指向符号流中的下一个符号。如果符号流不满足INTEGER PLUS INTEGER的结构，直接抛出异常。

让我们来回顾一下，你的解释器为了能够去计算算术表达式，它究竟做了些什么：

• 解释器接受了一个字符串作为输入，比如说$"3+5"$
• 解释器调用了expr方法，其从被get_next_token词法解析器返回的符号流中搜寻特定结构：INTEGER PLUS INTEGER。当找到了该结构后，解释器会将输入解释为两个整数（INTEGER）的和。在此刻，解释器知道它要做什么，求两个整数$3$和$5$的和。

恭喜你！你已经学会了去构建第一个解释器。