矩阵Matrix_矩阵行列表示用代码-优快云博客

题目：

(1)代表矩阵的行数rows(或m)、列数cols(或n)，以及矩阵的存储单元data(二维数组)；添加合适的属性(getters/setters)，注意访问修饰符的选择；

(2)一个参数为rows,cols的构造方法，实现初始化操作，并将矩阵元素全部置为0；

(3)一个参数为Matrix的构造方法，实现矩阵的深拷贝(即克隆出另一个一模一样的)；

(4)public void setElement(int row, int col, double value);方法，用于设置第row行，第col列元素的值；

(5)public Matrix add(Matrix m);方法，实现当前矩阵与m矩阵相加，并返回新的矩阵；若无法相加，则返回null；

(6)public Matrix minus(Matrix m);方法，实现当前矩阵减去m矩阵，并返回新的矩阵；若无法相减，则返回null；

(7)public Matrix multiple(Matrix m);方法，实现当前矩阵乘以m矩阵，并返回新的矩阵；若无法相乘，则返回null；

(8)public Matrix transposition();方法，实现矩阵转置，并返回新的矩阵；

(9)public void display();方法，打印当前矩阵。

实现该类，注意代码及封装的规范性。

编写一个测试程序，随机生成矩阵元素或者由程序中用常量设置（可不必由键盘输入），测试上述四则运算，打印运算结果。

思考：题中当四则运算无法操作时，返回null，这是否合适？是否有更好的解决方案？

解：

矩阵的四则运算按数学规则来编写，较容易，

以下是一个3*3矩阵和 3*3矩阵的四则运算输出结果：

初始矩阵

1.0 2.0 3.0

4.0 5.0 6.0

7.0 8.0 9.0

对方矩阵

1.0 2.0 3.0

4.0 5.0 6.0

7.0 8.0 9.0

加法：

2.0 4.0 6.0

8.0 10.0 12.0

14.0 16.0 18.0

减法：

0.0 0.0 0.0

乘法：

30.0 36.0 42.0

66.0 81.0 96.0

102.0 126.0 150.0

转置矩阵

1.0 4.0 7.0

2.0 5.0 8.0

3.0 6.0 9.0

可以通过计算得出，代码的四则运算没有大的问题；

思考：题中当四则运算无法操作时，返回null，这是否合适？是否有更好的解决方案？

分析：由于返回的是空指针，当输入的矩阵不符合运算要求但仍然进行display操作或其他操作时（操作者不知道是否会错误），会引发程序错误。

但是返回null是对的，但或许我们需要在Matrix类中的各个方法进行null检验，如果此时的操作数matrix是null时，就输出错误信息并返回。

以矩阵加法为例：

if (m == null) {

System.out.println("错误：输入的矩阵为null，无法进行加法运算。");

return null;

}

从而实现代码的健壮性。

测试：其中，m正确定义，n定义空；

Matrix n = null;
m.minus(n);
m.add(n);
m.multiple(n);

由于display和trans方法参数列表为空，那测试当m为空时，调用这两个方法时，出现了：

现在这两个方法内部输出调用信息：如果this == null ;输出错误信息；

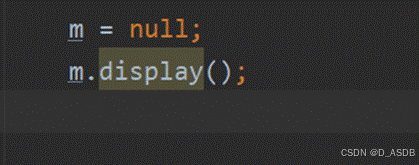
可见，程序直接退出了，没有输出错误信息。推断如果让一个空矩阵调用方法，是会直接返回错误的。因此就不需要再进行特判；

但是，乘法运算时，如果让两个3*4的矩阵相乘，会使mul 被赋值为 null ，从而导致在调用mul.display()时出错，但是又没法在display中进行错误处理，要怎么办？我的初步想法是直接对mul进行空指针判断，若不为空才进行display，否则就输出错误信息；

但是，这种方法又有些麻烦，每次在main中都要进行特判，那我想直接将display方法在四则运算中调用，不需要我们在main中调用，同理，包括加减法也是一样。

拿乘法为例：

public Matrix multiple(Matrix m){
    if (m == null)
    {
        System.out.println("错误：输入的矩阵为null，无法进行乘法运算。");
        return null;
    }
    if(this.cols != m.rows){
        System.out.println("两个矩阵不匹配，无法相乘");
        return null;
    }
    Matrix mul= new Matrix(this.rows,m.cols);
    for (int i = 0; i < this.rows; i++) {
        for (int j = 0; j < m.cols; j++) {
            double sum = 0;
            for (int k = 0; k < this.cols; k++) {
                sum += this.data[i][k] * m.data[k][j];
            }
            mul.data[i][j] = sum;
        }
    }
    mul.display(); //没有错误，就直接打印矩阵，减少在主函数中的null判定
    return mul;
}

下面是总代码：

public class Main {
    public static void main(String[] args) {
        int rows = 4 ,cols =4 ;
        Matrix m = new Matrix(rows,cols);
        int k = 1;
        for(int i = 0 ; i<rows;i++){
            for(int j = 0 ; j<cols;j++){
                m.setElement(i,j,k++);
            }
        }
        System.out.println("初始矩阵");
        m.display();
        Matrix n = new Matrix(m);
        System.out.println("对方矩阵");
        n.display();
        System.out.println("加法：");
        Matrix sum = m.add(n);
        System.out.println("减法：");
        Matrix minus = m.minus(n);
        System.out.println("乘法：");
        Matrix mul = m.multiple(n);
        System.out.println("转置矩阵");
        Matrix tran = m.transposition();
        tran.display();

    }
}

public class Matrix {
    private int rows;
    private int cols;
    private double[][] data ;

    public Matrix(int rows, int cols){
        this.rows = rows;
        this.cols = cols;
        this.data = new double[rows][cols];
        for(int i =0  ; i <this.rows ; i++){
            for(int j =0 ; j< this.cols ; j ++){
                this.data[i][j] = 0 ;
            }
        }
    }
    public Matrix(Matrix matrix){
        this.cols = matrix.cols;
        this.rows = matrix.rows;
        this.data = new double[rows][cols];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                this.data[i][j] = matrix.data[i][j];
            }
        }
    }
    public void setElement(int row, int col, double value){
        this.data[row][col] = value;
    }
    public Matrix add(Matrix m){
        if (m == null)
        {
            System.out.println("错误：输入的矩阵为null，无法进行加法运算。");
            return null;
        }
        if(m.cols != this.cols || m.rows != this.rows){
            return null;
        }
        Matrix sum = new Matrix(this.rows,this.cols);
        for(int i =0 ; i <this.rows ;i++){
            for(int j =0  ;j< this.cols ;j ++){
                sum.data[i][j] = this.data[i][j] + m.data[i][j];
            }
        }
        sum.display();
        return sum;
    }
    public Matrix minus(Matrix m){
        if (m == null)
        {
            System.out.println("错误：输入的矩阵为null，无法进行减法运算。");
            return null;
        }
        if(m.cols != this.cols || m.rows != this.rows){
            return null;
        }
        Matrix minu = new Matrix(this.rows,this.cols);
        for(int i =0 ; i <this.rows ;i++){
            for(int j =0  ;j<this.cols ;j ++){
                minu.data[i][j] = this.data[i][j] - m.data[i][j];
            }
        }
        minu.display();
        return minu;
    }
    public Matrix multiple(Matrix m){
        if (m == null)
        {
            System.out.println("错误：输入的矩阵为null，无法进行乘法运算。");
            return null;
        }
        if(this.cols != m.rows){
            System.out.println("两个矩阵不匹配，无法相乘");
            return null;
        }
        Matrix mul= new Matrix(this.rows,m.cols);
        for (int i = 0; i < this.rows; i++) {
            for (int j = 0; j < m.cols; j++) {
                double sum = 0;
                for (int k = 0; k < this.cols; k++) {
                    sum += this.data[i][k] * m.data[k][j];
                }
                mul.data[i][j] = sum;
            }
        }
        mul.display();
        return mul;
    }
    public Matrix transposition(){
        Matrix trans = new Matrix(this.cols , this.rows);
        for(int i = 0 ;  i< this.cols;i++){
            for(int j = 0 ; j<this.rows ;j++){
                trans.data[i][j] = this.data[j][i];
            }
        }
        return trans;
    }
    public void display(){

        for(int i =0 ; i <this.rows ;i++){
            for(int j =0  ;j<this.cols ;j ++){
                System.out.print(this.data[i][j]+" ");
            }
            System.out.println();
        }
    }
    public int getRows() {
        return rows;
    }

    public void setRows(int rows) {
        this.rows = rows;
    }

    public int getCols() {
        return cols;
    }

    public void setCols(int cols) {
        this.cols = cols;
    }

    public double[][] getData() {
        return data;
    }

    public void setData(double[][] data) {
        this.data = data;
    }
}