文章目录
paper:https://par.nsf.gov/servlets/purl/10301170
code: https://github.com/yenchenlin/nerf-pytorch
author: UC Berkeley; Google Research; UC San Diego
前置知识
- 相机内参与外参
相机的位置和朝向由相机的外参(extrinsic matrix)决定,投影属性由相机的内参(intrinsic matrix)决定。
1)相机外参:相机外参是一个4x4的矩阵 M M M ,其作用是将世界坐标系的点 P w o r l d = [ x , y , z , 1 ] P_{world}=[x,y,z,1] Pworld=[x,y,z,1]变换到相机坐标 P c a m e r a = M P w o r l d P_{camera}=MP_{world} Pcamera=MPworld下。相机外参也叫做world-to-camera(w2c)矩阵,它的逆矩阵被称为camera-to-world (c2w)矩阵,其作用是把相机坐标系的点变换到世界坐标系。NeRF主要使用c2w,这里详细介绍一下c2w的含义。c2w矩阵是一个4x4的矩阵,左上角3x3是旋转矩阵R,又上角的3x1向量是平移向量T。有时写的时候可以忽略最后一行[0,0,0,1]。

c2w矩阵的值直接描述了相机坐标系的朝向和原点,旋转矩阵的第一列到第三列分别表示了相机坐标系的X, Y, Z轴在世界坐标系下对应的方向;平移向量表示的是相机原点在世界坐标系的对应位置。举个例子,如果将c2w作用到(即左乘)相机坐标系下的X轴[1,0,0,0],Y轴[0,1,0,0], Z轴[0,0,1,0],以及原点[0,0,0,1](注意方向向量的齐次坐标第四维等于0,点坐标第四维等于1),我们会得到它们在世界坐标系的坐标表示如下。在下面可以看作,将c2w作用到相机坐标系下的X轴、Y轴、 Z轴、以及原点我们会依次得到c2w的四列向量。

2)相机内参:相机的内参矩阵将相机坐标系下的3D坐标映射到2D的图像平面,一般称其为K。K包含4个值,其中fx和fy是相机的水平和垂直焦距(对于理想的针孔相机,fx=fy),cx和cy是图像原点相对于相机光心的水平和垂直偏移量。有时若cx, cy未知时,我们可以用图像宽和高的1/2来近似。

缩放图像尺寸时,影响的只是相机的内参,外参以及其他参数不受影响。缩放图像后,内参的变化如下,具体的规则是:若将图像的宽缩放为原来的1/2,而高缩放为原来的的1/3,则fx、cx也缩放为原来的1/2,fy、cy也缩放为原来的1/2。

3)相机模型的一些基本概念:目前相机模型有线性模型和非线性模型两种。实际的成像系统是透镜成像的非线性模型。在这里,我们简要描述一下小孔成像模型,如下图所示:

视锥体(volume)是摄像机可见的空间,看上去像截掉顶部的金字塔,它的顶部是虚拟成像平面,底部是目标真实平面。可视化效果如下所示。这里面涉及一个重要的参数NF(near_far),它是视锥体的最远最近距离,也就是虚拟像平面和真实目标平面到相机中心的距离。

焦距的物理含义是相机中心到成像平面的距离,长度以像素为单位。视场角(field of view,fov)指的是。它们的关系如下。

4)齐次坐标:齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示,是指一个用于投影几何里的坐标系统。
**5)坐标系变换:**相机内参:用于将图像坐标系转换为相机坐标系。相机外参,用于将相机坐标系转换为世界坐标系。具体的做法是,先初始化一个图像坐标系下的grid,再用相机内参转换成相机坐标系的坐标(先转换成齐次坐标,再用内参转换成camera坐标),再用相机外参将相机坐标系转换成世界坐标系下的坐标。NDC坐标,TODO。
参考:对图像和相机参数进行同步缩放的方法及python实现代码、相机模型、NeRF代码解读-相机参数与坐标系变换。侵删。 - NeRF评价指标:PSNR、SSIM、LPIPS
1)PSNR:峰值信噪比(Peak Signal to Noise Ratio),一种评价图像质量的度量标准,衡量最大值信号和背景噪音之间的图像质量参考值。**PSNR的单位为dB,其值越大,图像失真越少。**一般来说,PSNR高于40dB说明图像质量几乎与原图一样好;在30-40dB之间通常表示图像质量的失真损失在可接受范围内;在20-30dB之间说明图像质量比较差;PSNR低于20dB说明图像失真严重。
2)SSIM:结构相似性指数(structural similarity index),一种用于量化两幅图像间的结构相似性的指标。与L2损失函数不同,SSIM仿照人类的视觉系统(Human Visual System,HVS)实现了结构相似性的有关理论,对图像的局部结构变化的感知敏感。SSIM从亮度、对比度以及结构量化图像的属性,用均值估计亮度,方差估计对比度,协方差估计结构相似程度。SSIM值的范围为0至1,越大代表图像越相似。如果两张图片完全一样时,SSIM值为1。
3)LPIPS:学习感知图像块相似度(Learned Perceptual Image Patch Similarity),也称为“感知损失”(perceptual loss),用于度量两张图像之间的差别。来源于CVPR2018的一篇论文《The Unreasonable Effectiveness of Deep Features as a Perceptual Metric》,该度量标准学习生成图像到Ground Truth的反向映射强制生成器学习从假图像中重构真实图像的反向映射,并优先处理它们之间的感知相似度。LPIPS 比传统方法(比如L2/PSNR, SSIM, FSIM)更符合人类的感知情况。LPIPS的值越低表示两张图像越相似,反之,则差异越大。 - 3D渲染:将场景定义(包括摄像机、灯光、剥面几何和材料)转换为模拟摄像机图像的过程称为渲染。 简单来说就是模拟相机的拍照过程,生成的结果是该视角下看到的一张照片。传统的3D渲染方法是光栅化 (rasterization),光线追踪(ray tracing)。
- Alpha合成(Alpha Compositing):在计算机图形学领域,Alpha合成是一种将图像与背景结合的过程,结合后可以产生部分透明或全透明的视觉效果。Alpha合成也叫阿尔法合成或透明合成。
- Alpha通道[5]是计算机图形学中的术语,指的是特别的通道,意思是“非彩色”通道,主要是用来保存选区和编辑选区。Alpha 没有透明度的意思,不代表透明度。opacity 和 transparency 才和透明度有关,前者是不透明度,后者是透明度。真正让图片变透明的不是Alpha 实际是Alpha所代表的数值和其他数值做了一次运算 。
- 阿尔法通道(α Channel或Alpha Channel)是指一张图片的透明和半透明度。例如:一个使用每个像素16比特存储的位图,对于图形中的每一个像素而言,可能以5个比特表示红色,5个比特表示绿色,5个比特表示蓝色,最后一个比特是阿尔法。
- 极限、导数和微分的关系[1]:
- 我们现在所学的体系,是按照先极限、再通过极限定义导数、再通过导数定义微分这个顺序来的。
- 极限的发明是为了解释无穷小的理论体系
- 导数是指函数在某一点处变化的快慢,是一种变化率[2],可以理解为切线的概率。如果 Δy/Δx 在Δx→0 时极限存在,则称函数 f(x)在 x0 处可导(仅在 x0 这一点处,并不保证在所有点处),并称这个极限为函数 y=f(x)在点x0 处的导数记为 f′(x0),即:
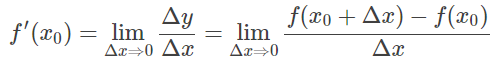
- 微分是指函数在某一点处(趋近于无穷小)的变化量,是一种变化的量
- 古典微分学:(1) dy和dx表示的是自变量和因变量的具体的变化; (2) 根据想象中的无穷小这个东西,定义了切线; (3) 然后将切线的斜率定义为导数
- 极限微分学与古典微分学的区别:
- 相同之处:都是表示微小变化的量
- 不同之处:(1) 古典微分是直接将变化的具体值定义成了微分,也就是dy=Δy,而极限微分学中是dy≈Δy。也就是在极限微分学中,微分是变化的逼近,而不是变化本身。(2) 微分是实实在在的一个量,是一个无穷小量(当变化趋近于0时)
- 求微分是求微分,求导是求导。积分就是求微分的和:定积分相当于求面积,不定积分相当于求原函数。
- 概率密度函数(PDF)、累积分布函数(CDF)、蒙特卡洛积分、离散空间采样、连续空间采样(基于逆变换采样)、连续空间采样(基于拒绝采样)、重要性采样及多重重要性采样。[3]
- 概率密度函数(PDF):是一个描述随机变量在某个确定的取值点附近的可能性的函数。横坐标表示自变量的取值,纵坐标纵坐标表示的并不是概率,而是概率密度,概率的表示形式为曲线下所围区域的面积。
- 累积分布函数(CDF):概率密度函数为 f X ( x ) f_X(x) fX(x)的一维随机变量所对应的累积分布函数为 F X ( x ) = ∫ − ∞ x f X ( t ) d t F_X(x)=\int_{-\infty }^{x} f_X(t)dt FX(x)=∫−∞xfX(t)dt,累积分布函数的值域为 [0, 1]。
- 蒙特卡洛积分: 简而言之就是,在求积分时,如果找不到被积函数的原函数,那么利用经典积分方法是得不到积分结果的,但是蒙特卡洛积分方法告诉我们,利用一个随机变量对被积函数进行采样,并将采样值进行一定的处理,那么当采样数量很高时,得到的结果可以很好的近似原积分的结果。这样一来,我们就不用去求原函数的形式,就能求得积分的近似结果。可以使用任意一个PDF来进行采样以计算蒙特卡洛积分。参考[4]。
- 对一个函数
f
(
x
)
f(x)
f(x)求积分,当其原函数
F
(
x
)
F(x)
F(x)不好求时,使用蒙特卡洛法对积分进行计算的过程描述如下:首先从区间[a,b]上对均匀分布的随机变量X连续取样N次,得到N个取样值
x
1
,
x
2
,
x
3
,
.
.
.
,
x
N
{x_1,x_2,x_3,...,x_N}
x1,x2,x3,...,xN,对每个取样值
x
i
(
i
=
1
,
2
,
3
,
.
.
.
,
N
)
x_i(i=1,2,3,...,N)
xi(i=1,2,3,...,N)计算
f
(
x
i
)
f(x_i)
f(xi)得到
f
(
x
1
)
,
f
(
x
2
)
,
f
(
x
3
)
,
.
.
.
,
f
(
x
N
)
{f(x_1),f(x_2),f(x_3),...,f(x_N)}
f(x1),f(x2),f(x3),...,f(xN),再计算它们的和
∑
i
=
1
N
f
(
x
i
)
\sum_{i=1}^{N} f(x_i)
∑i=1Nf(xi), 最后乘系数$\frac{b-a}{N} $即可得到对理论积分值的一个无偏估计。公式如下:
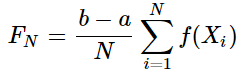
- 上述过程中
X
X
X被规定为与原积分区间相同的均匀分布随机变量。那么对于与原积分区间相同,但却不是均匀分布的一般随机变量,蒙特卡洛法也成立。定义如下,之前的要求不同,这里仅要求随机变量
X
X
X的概率密度分布函数
p
(
x
)
p(x)
p(x)已知且在
X
X
X的样本空间内
p
(
x
)
≠
0
p(x)≠0
p(x)=0。
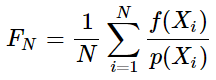
- 对一个函数
f
(
x
)
f(x)
f(x)求积分,当其原函数
F
(
x
)
F(x)
F(x)不好求时,使用蒙特卡洛法对积分进行计算的过程描述如下:首先从区间[a,b]上对均匀分布的随机变量X连续取样N次,得到N个取样值
x
1
,
x
2
,
x
3
,
.
.
.
,
x
N
{x_1,x_2,x_3,...,x_N}
x1,x2,x3,...,xN,对每个取样值
x
i
(
i
=
1
,
2
,
3
,
.
.
.
,
N
)
x_i(i=1,2,3,...,N)
xi(i=1,2,3,...,N)计算
f
(
x
i
)
f(x_i)
f(xi)得到
f
(
x
1
)
,
f
(
x
2
)
,
f
(
x
3
)
,
.
.
.
,
f
(
x
N
)
{f(x_1),f(x_2),f(x_3),...,f(x_N)}
f(x1),f(x2),f(x3),...,f(xN),再计算它们的和
∑
i
=
1
N
f
(
x
i
)
\sum_{i=1}^{N} f(x_i)
∑i=1Nf(xi), 最后乘系数$\frac{b-a}{N} $即可得到对理论积分值的一个无偏估计。公式如下:
- 离散空间采样:要对离散空间进行采样[3],一个简单的方法是:首先将表示概率的直方图堆叠起来(即:上图右边所示),然后生成一系列均匀分布的采样点,该采样点对应的值在哪个区间内,就返回对应的 x x x值。
- 连续空间采样(基于逆变换采样): 基于逆变换采样的方式适用于累积分布函数CDF可求解其逆函数的情况,具体过程参考[3]。
- 连续空间采样(基于拒绝采样): 若无法求解CDF的逆函数,则可使用拒绝采样
- 重要性采样 :上面所说,使用任意一个PDF来进行采样以计算蒙特卡洛积分,那么究竟哪种PDF是最好的呢?这就是重要性采样所回答的问题。参考[4],蒙特卡洛方法的估计值的不稳定来源于随机变量的取值不稳定,也就是说,如果 Y = f ( X i ) p ( X i ) Y=\frac{f(X_i)}{p(X_i)} Y=p(Xi)f(Xi) 因不同 X i X_i Xi的取值变化地越剧烈,就会造成 Y Y Y的方差较大,则会造成估计值的收敛速度越慢。这启示我们,若 p ( x ) p(x) p(x)的形状越接近 f ( x ) f(x) f(x),则有益于最终结果的收敛。这种思想就是重要性采样,即对积分值有重要贡献( f ( x ) f(x) f(x)较大)的被积函数区间,我们以较大概率生成处于这个区间附近的随机变量,用于快速逼近理论值。
NeRF原文阅读笔记
Nerf的网络和思路并不复杂,但其动机包含了很多光学和计算机图形学的知识,使对其进行改进形成了一定的门槛。本文主要是参考[6]对原文进行理解并记录。







总结
NeRF的成像是在相机视角位置成像的,也就是成像面是在光线发射位置。成像面(相机处)有h*w个像素,每个像素都有着对应的位置φ,伴随着相机内参,每个像素点也有着对应的观测方向θ。从这个像素点出发一条射线,中间可以采样n个点,每一个点都有一个空间坐标(x,y,z)。这样,所求图像的每一个像素都对应了一条射线,每条射线下有着n个输入(x, y, z, θ,φ),然后每一个点经过NeRF都会产生一个不透明度σ,和一个RGB值,将这条射线上点的不透明度从头开始累积到一定阈值,这一过程中的RGB的累积值就是所求图像上这一像素最后的颜色值。为每一个像素都执行以上过程,最终就合成了新视角下的图像。
参考文献
[1] https://www.zhihu.com/question/264955988
[2] https://www.zhihu.com/question/28684811
[3] https://zhuanlan.zhihu.com/p/396618080
[4] https://www.cnblogs.com/time-flow1024/p/10094293.html
[5] https://zhuanlan.zhihu.com/p/24415265
[6] https://zhuanlan.zhihu.com/p/360365941





















 1567
1567

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








