Prim算法

Concrete Content

最小生成树的Prim算法也是贪心算法的一大经典应用。Prim算法的特点是时刻维护一棵树，算法不断加边，加的过程始终是一棵树。

Prim算法过程：

一条边一条边地加， 维护一棵树。
初始 $E＝｛｝$空集合， $V=｛$任意节点$｝$
循环 $（n–1）$ 次，每次选择一条边$（v1,v2）$， 满足：$v1$ 属于 $V,v2$ 不属于 $V$。且 $（v1,v2）$权值最小。
$E=E+（v1,v2）$
$V=V+v2$
最终 $E$ 中的边是一棵最小生成树， $V$ 包含了全部节点。
最后，我们来提供输入输出数据，由你来写一段程序，实现这个算法;

输入

第1行：2个数N,M中间用空格分隔，N为点的数量，M为边的数量。$（2<=N<=1000,1<=M<=50000)$
第$2-M+1$行：每行3个数$S$ $E$ $W$，分别表示M条边的2个顶点及权值。$(1<=S,E<=N，1<=W<=10000)$

输出

输出最小生成树的所有边的权值之和。

输入示例

9 14
1 2 4
2 3 8
3 4 7
4 5 9
5 6 10
6 7 2
7 8 1
8 9 7
2 8 11
3 9 2
7 9 6
3 6 4
4 6 14
1 8 8

输出示例

37

请选取你熟悉的语言，并在下面的代码框中完成你的程序，注意数据范围，最终结果会造成Int32溢出，这样会输出错误的答案。

代码如下：
? (☄⊙ω⊙)☄

#include<iostream>
#include<cstring>
using namespace std;
const int inf=0x3f3f3f3f;
const int maxx=1100;
int e[maxx][maxx],dis[maxx];
bool book[maxx];
int n,m;
void init()
{
    for(int i=0; i<n; i++)
        for(int j=0; j<n; j++)
            if(i==j)e[i][j]=0;
            else
                e[i][j]=inf;
}
int prim(int e[][maxx],int n)
{
    int ans=0;
    memset(book,false,sizeof(book));
    book[0]=true;
    for(int i=1; i<n; i++)
        dis[i]=e[0][i];
    for(int i=1; i<n; i++)
    {
        int minn=inf,u=-1;
        for(int j=0; j<n; j++)
        {
            if(!book[j]&&dis[j]<minn)
            {
                minn=dis[j];
                u=j;
            }
        }
        if(ans==inf)
            return -1;
        ans+=minn;
        book[u]=true;
        for(int v=0; v<n; v++)
            if(!book[v])
                dis[v]=min(dis[v],e[u][v]);
    }
    return ans;
}
int main()
{
    while(cin>>m>>n)
    {
        init();
        for(int i=0; i<n; i++)
        {
            int a,b,c;
            cin>>a>>b>>c;
            if(e[a-1][b-1]>c)
                e[a-1][b-1]=e[b-1][a-1]=c;
        }
        cout<<prim(e,m)<<endl;
    }
    return 0;
}

以下图为例介绍Prim算法的执行过程。

Prim算法的过程从A开始 V = {A}, E = {}

选中边AF , V = {A, F}, E = {(A,F)}

选中边FB, V = {A, F, B}, E = {(A,F), (F,B)}

选中边BD, V = {A, B, F, D}, E = {(A,F), (F,B), (B,D)}

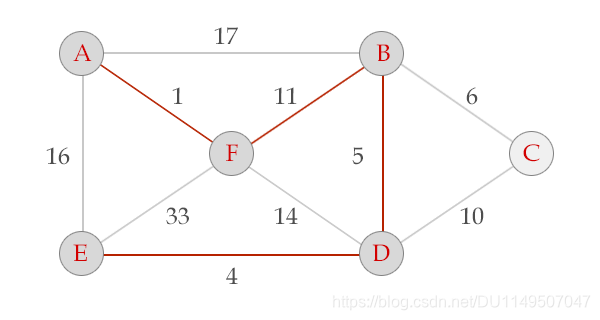
选中边DE, V = {A, B, F, D, E}, E = {(A,F), (F,B), (B,D), (D,E)}

选中边BC, V = {A, B, F, D, E, c}, E = {(A,F), (F,B), (B,D), (D,E), (B,C)}, 算法结束。