1 逻辑回归和线性回归的区别
-
线性回归方程为 z=f(x)=θ∗xz = f{(x)} = \theta*xz=f(x)=θ∗x,其中x为输入特征,θ\thetaθ为模型参数;损失函数记为L(θ)=∣∣y−f(x)∣∣22L(\theta)=||y-f(x)||_2^2L(θ)=∣∣y−f(x)∣∣22,通过梯度下降法求出最优的θ\thetaθ值。
-
逻辑回归(此处只针对二分类问题)是处理分类问题的,y的取值为0,1{0,1}0,1,需要对上述线性回归函数zzz做一步函数变化g(z)g(z)g(z),此时逻辑回归的方程可以写为g(z)=11+e−zg(z)=\frac{1}{1+e^{-z}}g(z)=1+e−z1
-
其中g(z)g(z)g(z)的导数可以记为:
g′(z)=ddz∗11+e−z=(11+e−z)2∗(e−z)=11+e−z∗(1−11+e−z)=g(z)∗(1−g(z))g'(z)= \frac{d}{dz} *\frac{1}{1+e^{-z}}=(\frac{1}{1+e^{-z}})^2*(e^{-z})=\frac{1}{1+e^{-z}}*(1-\frac{1}{1+e^{-z}})=g(z)*(1-g(z))g′(z)=dzd∗1+e−z1=(1+e−z1)2∗(e−z)=1+e−z1∗(1−1+e−z1)=g(z)∗(1−g(z))令g(z)g(z)g(z)中的z为:z=xθz=x\thetaz=xθ,这样就可以得到逻辑回归模型的一般形式hθ(x)=11+e−xθh_\theta(x)=\frac{1}{1+e^{-x\theta}}hθ(x)=1+e−xθ1
2 逻辑回归损失函数为交叉熵而不是MSE
-
按照逻辑回归的定义,假设我们的样本输出是0或者1两类。那么我们有
P(y=1∣x,θ)=hθ(x)P(y=1|x,\theta)=h_\theta(x)P(y=1∣x,θ)=hθ(x)
P(y=0∣x,θ)=1−hθ(x)P(y=0|x,\theta)=1-h_\theta(x)P(y=0∣x,θ)=1−hθ(x)
由于逻辑回归假设样本服从伯努利分布,因此上面两个式子可以合并为
P(y∣x,θ)=hθ(x)y(1−hθ(x))1−yP(y|x,\theta)=h_\theta(x)^y(1-h_\theta(x))^{1-y}P(y∣x,θ)=hθ(x)y(1−hθ(x))1−y ,其中y的取值是0或者1
得到了y的概率分布函数表达式,我们就可以用似然函数最大化来求解我们需要的模型系数θ\thetaθ,这里可以表示为:
L(θ)=∏i=1m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)L(\theta)= \prod_{i=1}^m (h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}L(θ)=∏i=1m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i),其中m为样本个数
对似然函数对数化取反后的表达式为:
J(θ)=−lnL(θ)=∑i=1m(y(i))ln(hθ(x(i)))+(1−y(i))ln(1−hθ(x(i))))J(\theta)=-lnL(\theta)=\sum_{i=1}^m (y^{(i)})ln(h_\theta(x^{(i)}))+(1-y^{(i)})ln(1-h_\theta(x^{(i)})))J(θ)=−lnL(θ)=∑i=1m(y(i))ln(hθ(x(i)))+(1−y(i))ln(1−hθ(x(i))))对θ\thetaθ求导可得 ∂J(θ)∂θ\frac{\partial J(\theta)}{\partial \theta}∂θ∂J(θ)
=−1m∑i=1m[y(i)hθ(x(i))∂hθ(x(i))∂θ+(1−y(i))1−hθ(x(i))−∂hθ(x(i))∂θ]= -\frac{1}{m}\sum_{i=1}^m[\frac {y^{(i)}}{h_\theta(x^{(i)})}\frac{\partial h_\theta(x^{(i)})}{\partial \theta}+\frac{(1-y^{(i)})}{1-h_\theta(x^{(i)})}\frac{-\partial h_\theta(x{(i)})}{\partial \theta} ]=−m1∑i=1m[hθ(x(i))y(i)∂θ∂hθ(x(i))+1−hθ(x(i))(1−y(i))∂θ−∂hθ(x(i))]
=−1m∑i=1m[y(i)hθ(x(i))(hθ(x(i))(1−hθ(x(i))x(i)+(1−y(i))1−hθ(x(i))(hθ(x(i))(1−hθ(x(i))x(i)]=-\frac{1}{m}\sum_{i=1}^m[\frac {y^{(i)}}{h_\theta(x^{(i)})}(h_\theta(x^{(i)})(1-h_\theta(x^{(i)})x^{(i)}+\frac{(1-y^{(i)})}{1-h_\theta(x^{(i)})}(h_\theta(x^{(i)})(1-h_\theta(x^{(i)})x^{(i)} ]=−m1∑i=1m[hθ(x(i))y(i)(hθ(x(i))(1−hθ(x(i))x(i)+1−hθ(x(i))(1−y(i))(hθ(x(i))(1−hθ(x(i))x(i)]
=−1m∑i=1my(i)x(i)−hθ(x(i))x(i)=-\frac{1}{m}\sum_{i=1}^my^{(i)}x^{(i)}-h_\theta(x^{(i)})x^{(i)}=−m1∑i=1my(i)x(i)−hθ(x(i))x(i)
=−1m∑i=1m[y(i)−hθ(x(i))]x(i)=-\frac{1}{m}\sum_{i=1}^m [y^{(i)}-h_\theta(x^{(i)})]x^{(i)}=−m1∑i=1m[y(i)−hθ(x(i))]x(i)
用矩阵表示,且加入学习率以后,θ\thetaθ的梯度下降更新公式可以记为:
θ:=θ−XT(hθ(X)−Y)\theta := \theta - X^T(h_\theta(X)-Y)θ:=θ−XT(hθ(X)−Y) -
若采用MSE作为损失函数,则
J(θ)=12m∑i=1m[hθ(x(i))−y(i)]2J(\theta)=\frac{1}{2m}\sum_{i=1}^m [h_\theta(x^{(i)})-y^{(i)}]^2J(θ)=2m1∑i=1m[hθ(x(i))−y(i)]2,
此时的J(θ)J(\theta)J(θ)关于参数θ\thetaθ是非凸函数,存在多个局部解;而交叉熵函数则是关于参数θ\thetaθ的高阶连续可导的凸函数,因此可以根据凸优化理论求的最优解。
J(θ)=12m∑i=1m[hθ(x(i))−y(i)]2J(\theta)=\frac{1}{2m}\sum_{i=1}^m [h_\theta(x^{(i)})-y^{(i)}]^2J(θ)=2m1∑i=1m[hθ(x(i))−y(i)]2,
此时的J(θ)J(\theta)J(θ)关于参数θ\thetaθ是非凸函数,存在多个局部解;而交叉熵函数则是关于参数θ\thetaθ的高阶连续可导的凸函数,因此可以根据凸优化理论求的最优解。 -
MSE求梯度
∂J(θ)∂θ=−1m∑i=1m[y(i)−hθ(x(i))]∗[hθ(x(i))(1−hθ(x(i))]x(i)\frac{\partial J(\theta)}{\partial \theta}= -\frac{1}{m}\sum_{i=1}^m [y^{(i)}-h_\theta(x^{(i)})]*[h_\theta(x^{(i)})(1-h_\theta(x^{(i)})]x^{(i)}∂θ∂J(θ)=−m1∑i=1m[y(i)−hθ(x(i))]∗[hθ(x(i))(1−hθ(x(i))]x(i)
<=0.25(−1m∑i=1m[y(i)−hθ(x(i))]∗x(i))<=0.25 (-\frac{1}{m}\sum_{i=1}^m [y^{(i)}-h_\theta(x^{(i)})]*x^{(i)})<=0.25(−m1∑i=1m[y(i)−hθ(x(i))]∗x(i)),
即MSE的梯度值<=0.25交叉熵梯度值,容易造成梯度消失。即MSE的梯度值<=0.25交叉熵梯度值,容易造成梯度消失。
3 逻辑回归的注意点
- 可解释性强(优点)
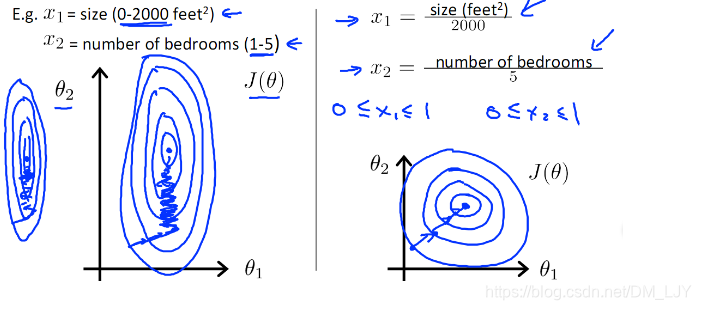
- 由于z=xθz=x\thetaz=xθ,其中求最优θ\thetaθ值是会受到xxx的取值影响(如有两个特征数量级x1/x2x1/x2x1/x2=10000,则模型在优化的过程中,x1x1x1的影响量将是x2x2x2的10000倍,在学习过程中会忽略x2x2x2的影响,导致模型的学习效果变差)。另外,类似xθx\thetaxθ类型的机器学习模型,归一化后使得更加容易找到最优解。如归一化前和归一化后的搜索空间和搜索过程如下所示:
- 逻辑回归没有特征的交叉,难以实现个性化(针对传统的逻辑回归而言,后续改进模型也加入了交叉项,可以参考FM)
即z=θ0+θ1x1+θ2x2z=\theta_0+\theta_1x_1+\theta_2x_2z=θ0+θ1x1+θ2x2,其中x1和x2是两类特征(可以分别看做产品特征和用户特征),对于同一批产品,x2x_2x2的取值实际不会对这批产品的结果产生影响。举例如下:取θ0=0\theta_0=0θ0=0, θ1=1\theta_1=1θ1=1, θ2=1\theta_2=1θ2=1,该批产品有三件,对应特征分别为
| 产品 | x1x_1x1 | x21x_{21}x21 | x22x_{22}x22 |
|---|---|---|---|
| H1 | 100 | 300 | 100 |
| H2 | 200 | 300 | 100 |
| H3 | 300 | 300 | 100 |
对于用户1
①z11=100∗1+300=400z_11=100*1+300=400z11=100∗1+300=400
②z21=200∗1+300=500z_21=200*1+300=500z21=200∗1+300=500
③z31=300∗1+300=600z_31=300*1+300=600z31=300∗1+300=600
对于用户2
①z12=200∗1+100=300z_12=200*1+100=300z12=200∗1+100=300
②z22=100∗1+200=400z_22=100*1+200=400z22=100∗1+200=400
③z32=200∗1+300=500z_32=200*1+300=500z32=200∗1+300=500
该批产品的得分相对顺序,不会受到用户特征的影响








 本文详细解析了逻辑回归与线性回归的区别,重点介绍了逻辑回归的模型形式、损失函数选择及其背后的数学原理,同时探讨了逻辑回归的特性与应用限制。
本文详细解析了逻辑回归与线性回归的区别,重点介绍了逻辑回归的模型形式、损失函数选择及其背后的数学原理,同时探讨了逻辑回归的特性与应用限制。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








