算法每日一题——蜗牛（蓝桥杯Java2023B组省赛）

本文链接：https://blog.youkuaiyun.com/DBxiaozuo/article/details/146926054

算法每日一题——蜗牛（蓝桥杯Java2023B组省赛）

题目介绍

在这里插入图片描述

题目分析

经典选与不选问题，每一次蜗牛都可以选择走或不走传送门，所以直接考虑动态规划。
可能有的人会陷入一个误区，如果蜗牛走传送门，那么接下来到坐标（xi+1，b【i+1】），不走传送门则到（xi+1，0），这样不会违反无后序性吗？但是其实无所谓，每一次DP都会考虑到上次走没走传送门，然后根据策略选择不同的状态转移方程。

设计DP数组

DP【n】【2】，n表示柱子数量，2存储行动策略

初始化DP数组

第一根柱子没得选，必须爬过去
dp【0】【0】 = a【0】
dp【0】【1】 = a【0】
这样就初始化完毕了

构筑状态转移方程

除开第一跟柱子，有四种情况
1. 上一次没走传送门，这一次走传送门：说明上次爬到柱子底部，所以我们直接向上爬找传送门
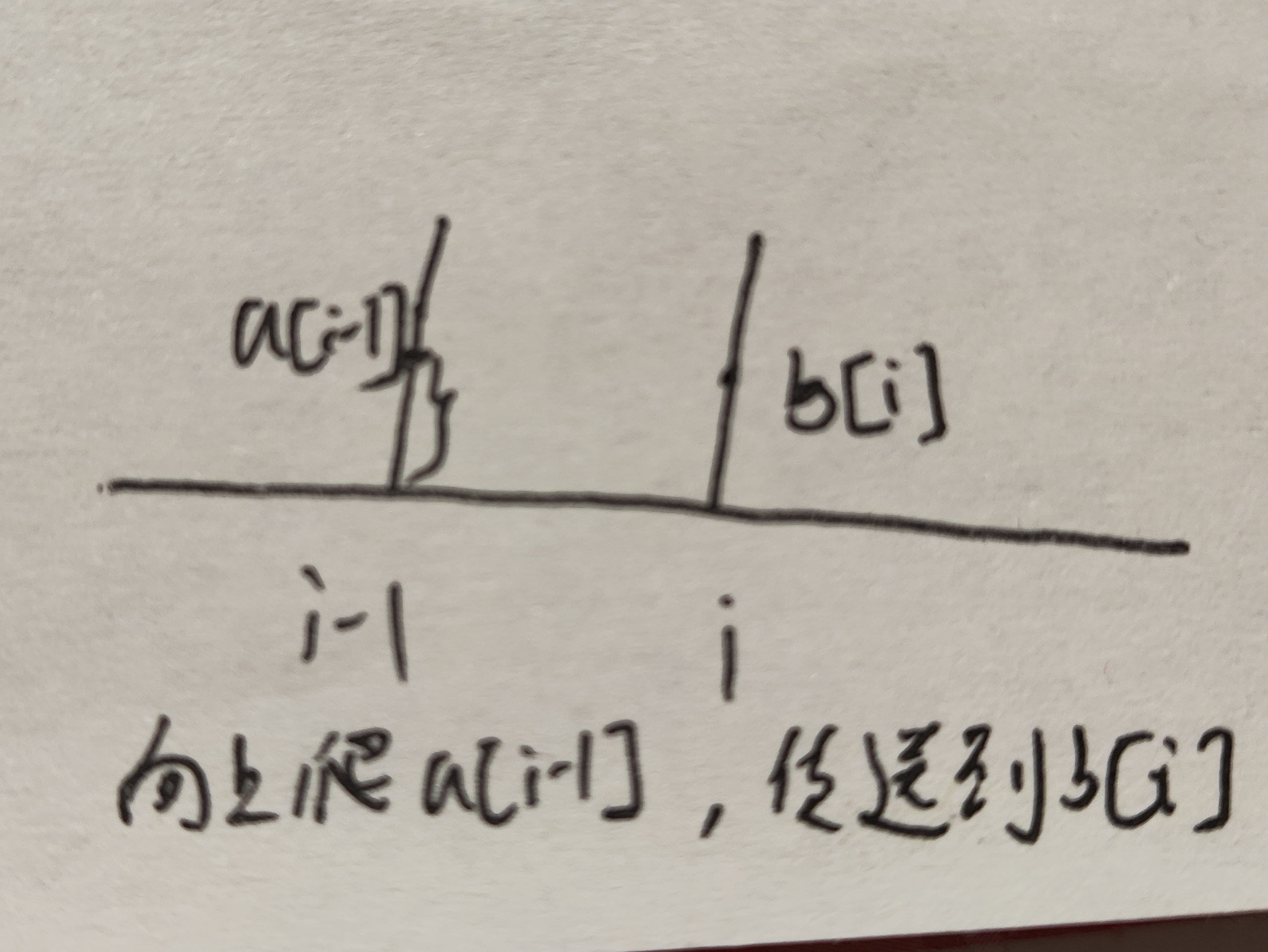
2. 上一次走传送门，这一次也走传送门：走传送门了，所以在柱子上挂着呢，找新传送门的位置就行，判断一下是上爬还是下爬
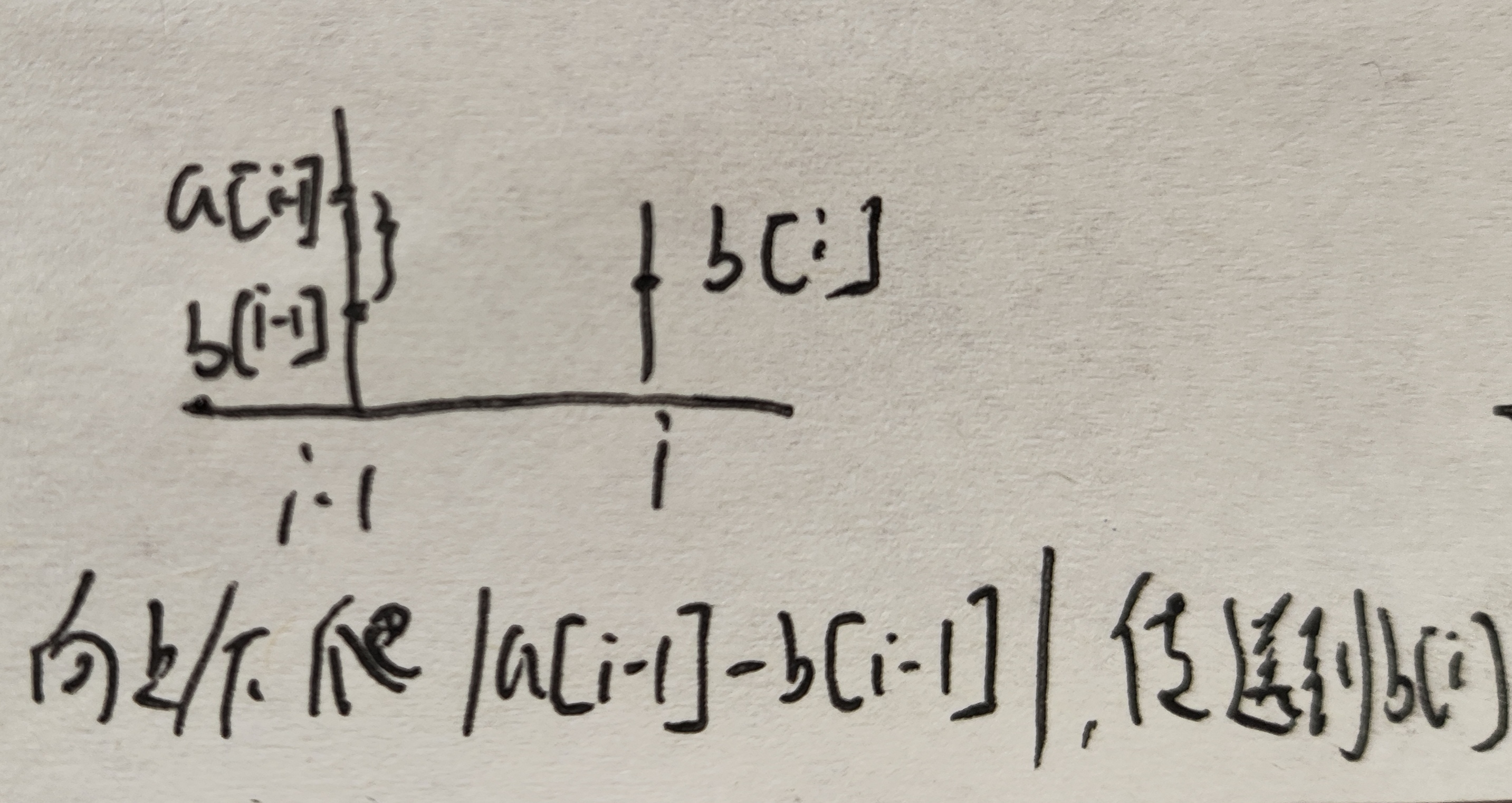
3. 上一次没走传送门，这一次也不走传送门：那就很简单了，一直在横坐标上移动，直接走柱间距就行
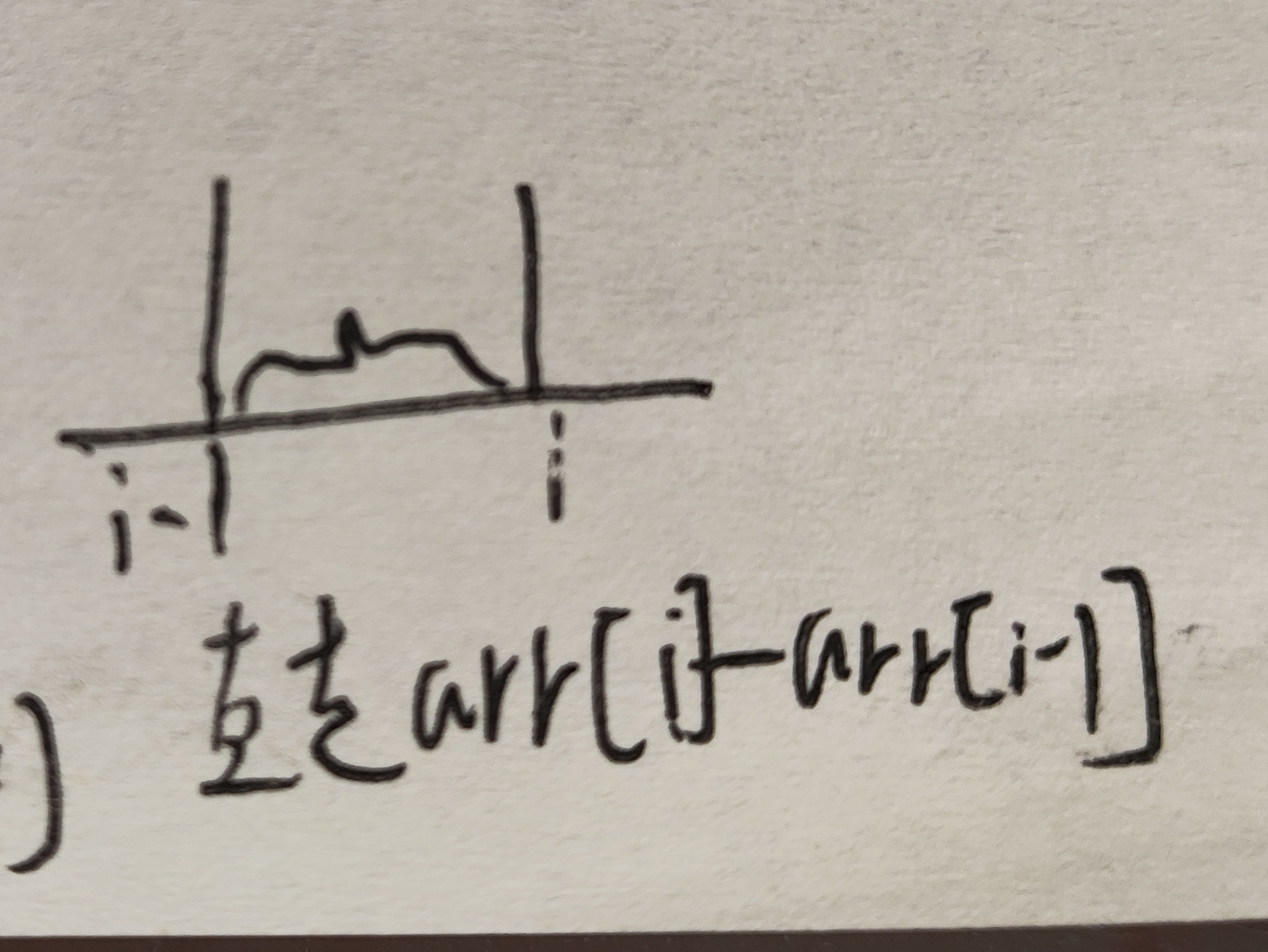
4. 上一次走传送门，这一次不走传送门：先从传送门终点下来，再走到下一根柱子
注意如果是走传送门到最后一根柱子，那还得从传送门上爬下来
最后得到状态转移方程：

double dis = b[i-1] > a[i-1] ? (b[i-1]-a[i-1])/1.3 : (a[i-1]-b[i-1])/0.7;
//去第i个柱子走传送门
dp[i][1] = min(dp[i-1][0] + a[i-1]/0.7 ,
               dp[i-1][1] + dis);

//去第i个柱子不走传送门
dp[i][0] = min(dp[i-1][0] + arr[i] - arr[i-1] ,
               dp[i-1][1] + arr[i] - arr[i-1] + b[i-1]/1.3);
        
//如果走传送门到终点，那就还要往下爬
if(i == n) dp[i][1] += b[i]/1.3;

代码实现

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

double dp[100010][2];//dp数组记录用时
double arr[100010];//arr记录柱子x轴坐标
ll a[100010];//a记录起点
ll b[100010];//b记录终点
ll n;//柱子的数量

int main(){
    //输入数据
    cin>>n;
    for(int i = 1; i <= n; i++){
        cin>>arr[i];
    }
    for(int i = 1; i < n; i++){
        cin>>a[i]>>b[i+1];
    }
    b[1] = 0; a[n] = 0;
    //初始化dp
    dp[1][0] = arr[1];
    dp[1][1] = arr[1];
    //填表
    for(int i = 2; i <= n; i++){
        //去第i个柱子走传送门
        double dis = b[i-1] > a[i-1] ? (b[i-1]-a[i-1])/1.3 : (a[i-1]-b[i-1])/0.7;
        dp[i][1] = min(dp[i-1][0] + a[i-1]/0.7 ,
                       dp[i-1][1] + dis);

        //去第i个柱子不走传送门
        dp[i][0] = min(dp[i-1][0] + arr[i] - arr[i-1] ,
                       dp[i-1][1] + arr[i] - arr[i-1] + b[i-1]/1.3);
        
        //如果走传送门到终点，那就还要往下爬
        if(i == n) dp[i][1] += b[i]/1.3;    

        //cout<<dp[i][0]<<' '<<dp[i][1]<<endl;
    }
    double ans = min(dp[n][1], dp[n][0]);
    ans = round(ans*100)/100;
    printf("%.2f",ans);
}