贪吃蛇DFS补题（2.26更新极大值剪枝的拓展，防止TLE）

提示：今天下午打了牛客的最后一场比赛，其中贪吃蛇这道题困扰了我接近一小时，这道题说白了是个简单的DFS，套用模版就行了，但是不知道为啥就是过不了！

题目

链接：https://ac.nowcoder.com/acm/contest/9986/I
来源：牛客网

无限增长的贪吃蛇小游戏：

在一个n*m的迷宫中，有一条小蛇，地图中有很多围墙，猥琐的出题者用“#”表示，而可以走的路用“.”表示，小蛇他随机出生在一个点上，出生点表示为“S”，他想抵达的终点表示为“E”，小蛇有一个奇怪的能力，他每走一格便会增长一格，即他走了一格后，他的尾巴不会缩回。

小蛇想知道他怎么到达他想去的地方，请你帮助他。

PS：每格长1米，贪吃蛇规定不能撞墙，不能咬自己的身体。
输入描述:
第一行：输入N,M；

第二行：输入S的坐标Xs，Ys，E的坐标Xe，Ye;

后面的N行：

每行输入M个数，描述每一行的情况。

输出描述:
输出一个数，小蛇到达终点的最短距离（单位：cm），若无法达到，输出-1
示例1
输入
复制
3 3
1 1 3 3
.#.
.#.
…
输出
复制
400

---

提示：对于 100% 的数据：1\le n,m\le 1001≤n,m≤100 ，保证起点不是围墙。

二、AC代码

代码如下：

#include<bits/stdc++.h>
using namespace std;
int N,M;
int Xs,Ys,Xe,Ye;
int mi=0x3f3f3f3f;
char m[105][105];
int vis[105][105];
int t[4][2]={{0,-1},{0,1},{1,0},{-1,0}};
void dfs(int x,int y,int step){
	//弹出条件也就是找到终点
    if(x==Xe&&y==Ye){
        mi=min(mi,step);
    }
    for(int i=0;i<4;i++){
    	//四个方向的行走递归
        int xx=x+t[i][0];
        int yy=y+t[i][1];
        //确保这条路是能走的，而且没有跳出边界
        if(xx>=1&&xx<=N&&yy>=1&&yy<=M&&m[xx][yy]!='#'&&vis[xx][yy]==0){
        	//确保(xx,yy)这条路走和不走都能遍历
            vis[xx][yy]=1;
            dfs(xx,yy,step+1);
            vis[xx][yy]=0;
        }
    }
}

int main(){
    cin>>N>>M;
    cin>>Xs>>Ys>>Xe>>Ye;
    for(int i=1;i<=N;i++){
        for(int j=1;j<=M;j++){
            cin>>m[i][j];
        }
    }
    dfs(Xs,Ys,0);
    //如果找不到就说明mi没有找到更短的，直接输出-1
    if(mi==0x3f3f3f3f)cout<<-1;
    else cout<<mi*100;
	return 0;
}

总结

其实要注意的就是判断完后将当前vis标记为1，进行递归，然后将vis再调回0的状态

说实话，只要dfs会用，这道题不难

---

2.26小更新哈

关于极大值剪枝的拓展 介绍一下

我们先从题目引入：

蒜头君有 nn 个玩具要分给 n 个小朋友，每个小朋友对每个玩具都有一个喜爱值,第 i个小朋友对第 j 个玩具的喜爱值是 a[i][j]

现在蒜头君希望将玩具都分下去，但是希望小朋友们的喜爱值和可以最大，请你帮他计算一下，如何分配可以使得喜爱值之和达到最大？

输入格式
输入第一行包含一个正整数 n，表示有 n 个玩具和 n 个小朋友。

第二行至第 n+1 行共 n 行，每行有 n 个以空格分隔的正整数。第 i+1 行的第 j个数 k(1≤k≤1000)，表示第 i 个小朋友对第 j 个玩具的喜爱值为k。

输出格式
输出只有一行，该行只有一个正整数，表示求得的喜爱值之和的最大值。

数据范围
对于 50% 的数据，1≤n≤9

对于 100% 的数据，1≤n≤17

输出时每行末尾的多余空格，不影响答案正确性

样例输入

3
10 6 8
9 2 3
1 7 2

样例输出

24

---

说明：这道题其实稍微读题就会发现是一道DFS可以解决的问题，唯一需要担心的是在最大值17^3的范围内可能会超时（其实一定会），这时候我们引入一个极大值剪枝的概念。

在输入时，求出了每一行的最大值，剪枝的关键就是如果曾经搜索到的最大值>=当前搜索到的值+还没搜索行的最大值之和（后缀最大值），就可以结束搜索了，因为在搜索下去，也不可能搜到比上一次大的（当前搜索的值+剩下的最大值<=上次搜索的最大值），极小值剪枝技巧也是类似。

光看文字可能有点烦有点难理解，接下来我们把上述例子做一个解释。
根据这个数据我们建立好图map

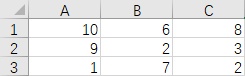
首先我们画出这个树

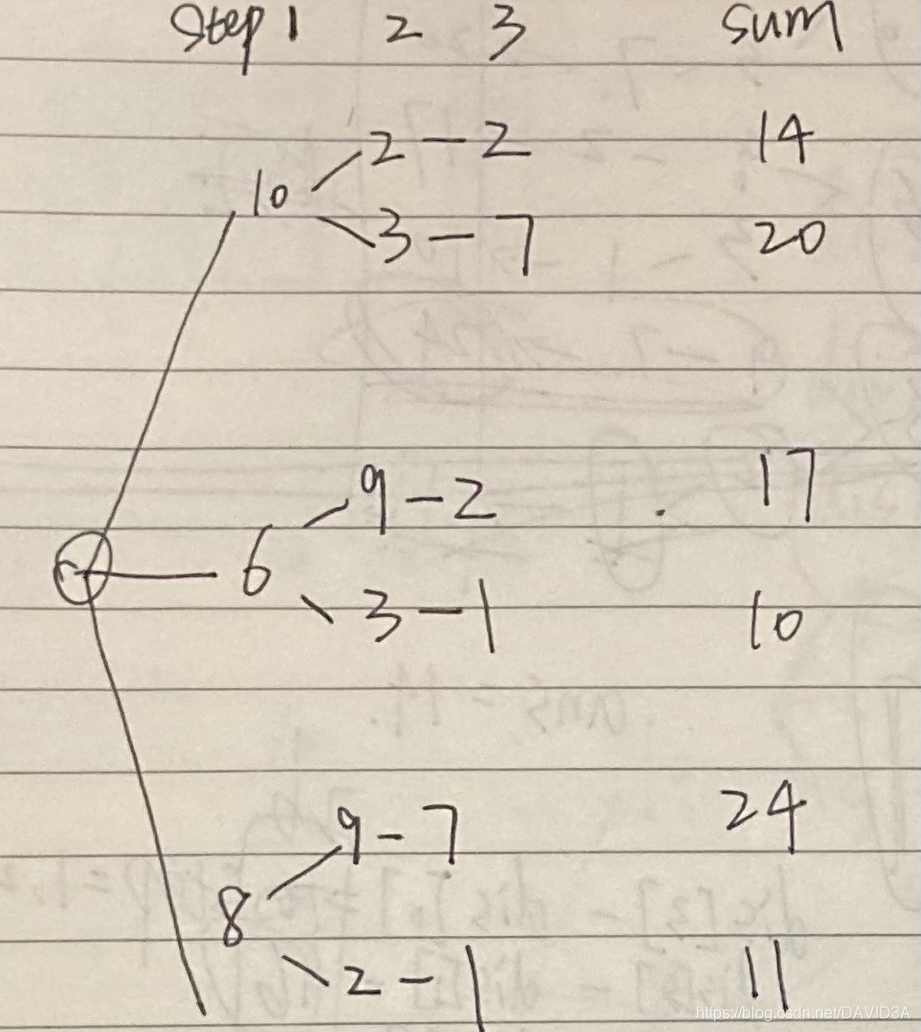
我们可以看到sum值最大是24，当然这是我们全部画出来的结果，那么根据这个算法，我们能有哪些改进呢？

让我们回忆一下，我们之前建立的dis数组的作用，我们发现我们把每行最大值相加存放在dis数组里，我们来看看里面的值(从0到3)【0，10，19，26】。其实这个dis数组就标记了还没搜索行的最大值之和。

比如说我们走到8-9-7这一行，我们当前ans值更新为了24，从上帝视角来看这是全图最大的情况，于是在走下一个dfs内嵌的时候，sum值在step=1的时候是8，此时我们判断（ans>=sum+dis[n]-dis[step-1]）是否能成立。（dis[n]-dis[step-1]在当前情况是16，说明后边最大也只能大到16，当然实际是2+1=3，那么显然8+16==24这个值已经出现过了，后面的算法也就没有必要再执行下去了，于是直接return）

就这样，我们通过及时的跳出实现了缩短算法时间，防止了TLE
极小值剪枝同理

这里贴一下AC代码，便于复习

#include<bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 1e6+5;
int mp[20][20],vis[30],m,n;
int dis[30],ans;
void dfs(int step,int sum)
{
    if(step==n+1) {
        ans = max(ans, sum);
    }
    if(ans>=sum+dis[n]-dis[step-1])
        return;

        for(int i=1;i<=n;i++)
        {
            if(!vis[i]) {
                vis[i] = 1;
                dfs(step + 1, sum + mp[step][i]);
                vis[i] = 0;
            }

        }

}
int main(){


    while(~scanf("%d",&n))
    {
        memset(mp,0,sizeof mp);
        memset(vis,0,sizeof vis);
        memset(dis,0,sizeof dis);
        ans = -1;
        for(int i=1;i<=n;i++) {
            m = -1;
            for (int j = 1; j <= n; j++) {
                scanf("%d", &mp[i][j]);
                m = max(m, mp[i][j]);
            }
            dis[i] = dis[i-1] + m;
        }
        dfs(1,0);
        cout << ans << endl;
    }
    return 0;
}