Tensorflow（二十二） —— 函数优化

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt 
from matplotlib import cm
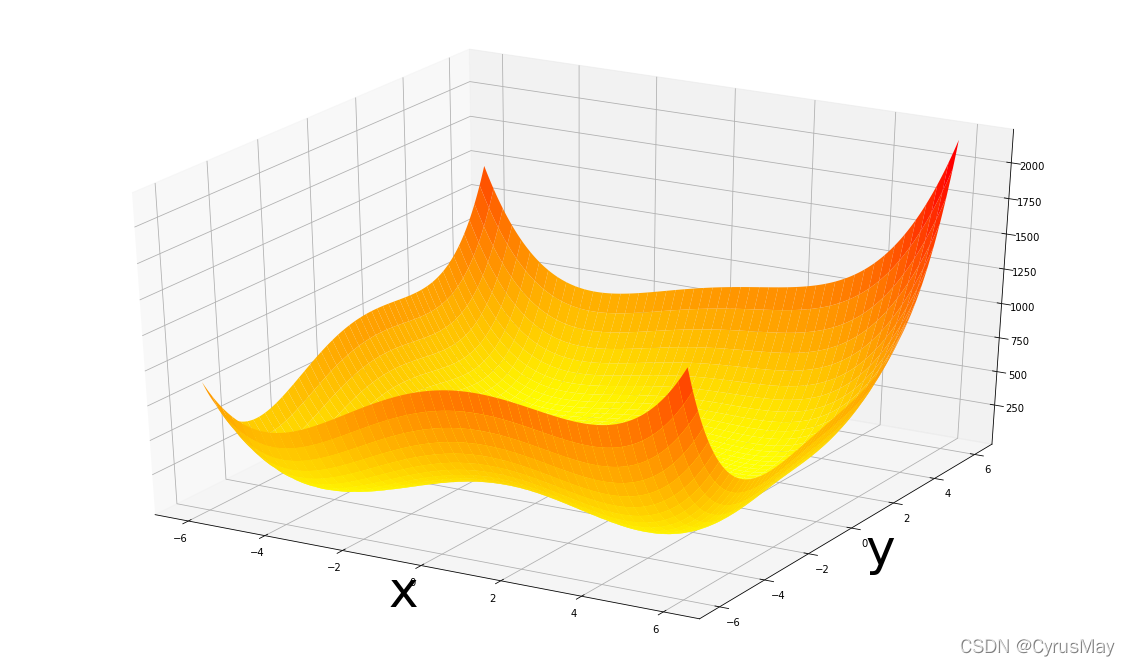
def my_func(x):
    return (x[0]**2 + x[1]-11)**2 + (x[0] + x[1]**2 - 7)**2

x = np.linspace(-6,6,500)
y = np.linspace(-6,6,500)
X,Y = np.meshgrid(x,y)
Z = my_func([X,Y])

fig = plt.figure(figsize=[20,12],dpi = 72)
ax = fig.add_subplot(111,projection = "3d")
ax.plot_surface(X,Y,Z,cmap = cm.autumn_r)

ax.set_xlabel("x",size = 50)
ax.set_ylabel("y",size = 50)

x = tf.constant([4.,4.])
record_x = []
record_y = []
for step in range(100):
    record_x.append(x[0])
    record_y.append(x[1])
    with tf.GradientTape() as tape:
        tape.watch([x])
        y = my_func(x)
    grads = tape.gradient(y,[x])[0]
    x -= 0.01*grads
route = [np.array(record_x),np.array(record_y)]
route_z = my_func(route)
fig = plt.figure(figsize=[20,12],dpi = 72)
ax = fig.add_subplot(111,projection = "3d")
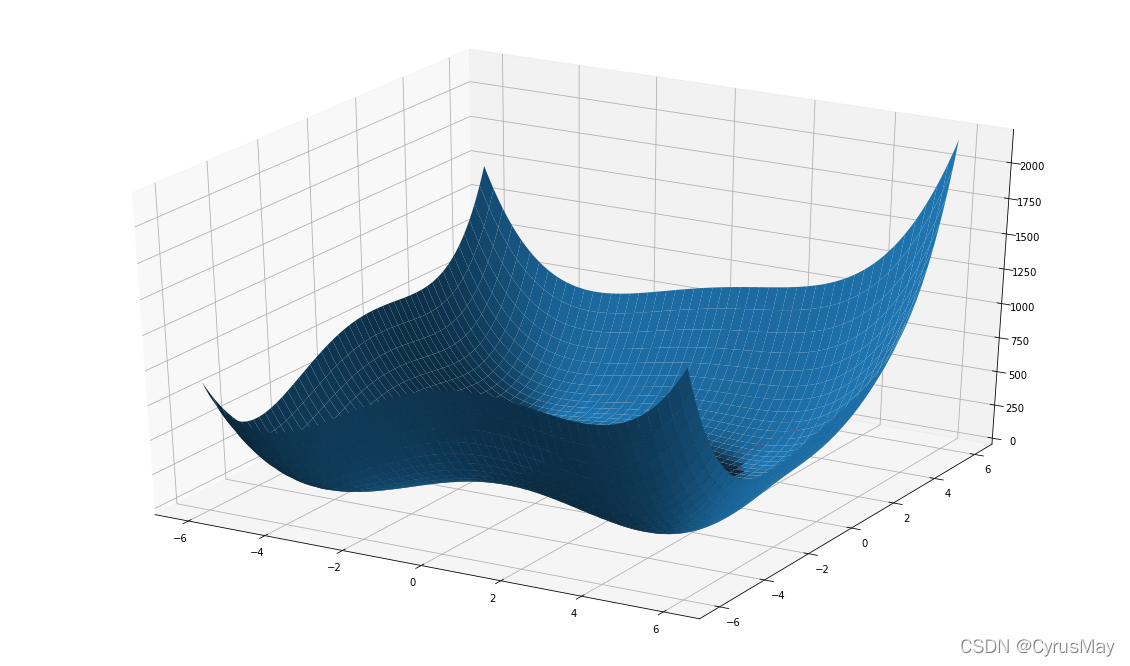
ax.plot_surface(X,Y,Z)
ax.plot(route[0],route[1],route_z,marker = "*",color="r")

本文为参考龙龙老师的“深度学习与TensorFlow 2入门实战“课程书写的学习笔记

by CyrusMay 2022 04 17