Letcode题解 —— 4. 寻找两个正序数组的中位数

最新推荐文章于 2025-12-03 12:28:21 发布

原创最新推荐文章于 2025-12-03 12:28:21 发布 · 686 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#python #数据结构 #算法 #letcode

Letcode 专栏收录该内容

1 篇文章

订阅专栏

本文详细介绍了如何解决LeetCode上的4号问题——寻找两个正序数组的中位数。通过二分查找的方法，实现了在O(log(m+n))的时间复杂度内找到合并后的中位数。解题思路包括将数组分为左右两部分，并利用二分查找确定分界线，确保左右两边元素满足中位数条件。示例和代码展示进一步解释了算法的具体实现过程。

1.题目

题目链接
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。
示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

2. 解题思路

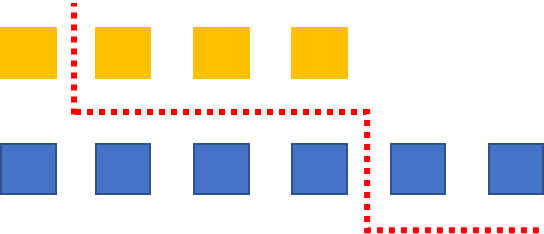
将两个数组分别分成左右两部分，左右两部分组合在一起分别为中位数的两边，且左边元素小于右边元素。在查找分界线位置时可使用二分查找的思想。

保持上方数组长度小于等于下方数组，利于使用二分查找时，下方数组不越界。
注意考虑边界条件。

3. 参考代码

    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        if len(nums2) < len(nums1):
            nums1,nums2 = nums2,nums1
        m = len(nums1)
        n = len(nums2)
        if m==0 and n == 0:
            return None
        elif m == 0:
            return 0.5 * (nums2[(n-1)//2] + nums2[n//2])
        elif n == 0:
            return 0.5 * (nums1[(m-1)//2] + nums1[m//2])
        left = 0
        right = m
        while left <= right:
            i = (left+right)//2
            j = (m+n+1)//2 - i
            l1 = float("-inf") if i == 0 else nums1[i-1]
            r1 = float("inf") if i == m else nums1[i]
            l2 = float("-inf") if j == 0 else nums2[j-1]
            r2 = float("inf") if j == n else nums2[j]
            if l1 > r2:
                right = i - 1
            elif r1 < l2:
                left = i + 1
            else:
                break
        return max(l1,l2) if (m+n)%2 else (max(l1,l2)*0.5 + min(r1,r2)*0.5)