1、搜索树
1.1 概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
1、若它的左子树不为空,则左子树上所有节点的值都小于根节点的值。
2、若它的右子树不为空,则右子树上所有节点的值都大于根节点的值。
3、它的左右子树也分别是二叉搜索树。
下图是一棵二叉搜索树,它的中序遍历就是升序的。
后面我们将通过代码来实现二叉搜索树,下面是创建二叉搜索树节点的代码:
static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root = null;
1.2 代码实现—查找
因为二叉搜索树在根的左边的节点都比根小,在根右边的节点比根大,我们可以设置一个节点cur==root,如果当前节点的值大于要找的值,那么就让cur往左边走,如果当前节点的值小于要找的值,那么让cur往右边走,如果要找的值等于当前cur的值返回true。
 1.3 代码实现—插入
1.3 代码实现—插入
由概念:我们可知二叉搜索树是一棵有序的树。而如果我们要在二叉搜索树上插入节点,那么插入的一定是叶子节点,所以我们可以和上面的查找方法一样,定义一个cur下标,如果cur的值比要插入的值小,就让cur往右边走;如果cur的值比要插入的值大,就让cur往左边走,与查找不同的是当走到相同的值时,则需要抛出异常(因为二叉搜索树是不允许出现节点值一样的情况的)。这里还需要注意,我们需要设置一个parent节点记录parent的值,不然当cur遍历完二叉搜索树时,我们无法找到要插入位置当前父亲的值。最后,我们刚才讨论的是树中有节点的情况,如果当前树是空树,我们只需要新建一个节点插入即可。(如果不讨论空树的情况会导致空指针异常)。


//插入的位置一定是叶子
//不能插入相同的数据的
public void insert(int val) {
TreeNode node = new TreeNode(val);
//注意判断根空不空,防止空指针异常
if(root == null){
root = node;
return;
}
TreeNode cur = root;
TreeNode parent = null;
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
}else{
throw new valError("输入的val在二叉搜索树中已经存在");
}
}
if(parent.val < val){
parent.right = node;
}else{
parent.left = node;
}
}1.4 代码实现—删除(难点)
引入:
二叉搜索树的删除是一项难点,如图,如果要删除值为8的节点,只需要让9连到7的右边就可以了。

替罪羊法
但如果要删除的是左边值为1的节点呢?
删除了1的节点后,3的左边应该连接值为0的节点还是值为2的节点呢?解决的方法是使用替罪羊法:首先,找到左子树最右边的节点或者右子树最左边的节点(这里我们采用找到右子树最左边的节点进行讲解),然后我们用找到的这个节点覆盖掉原来要删除的值,然后将右子树最左边的节点进行删除。注意:这里删除的节点其实是我们找到的节点,而我们想要删除的节点只是被替换了。
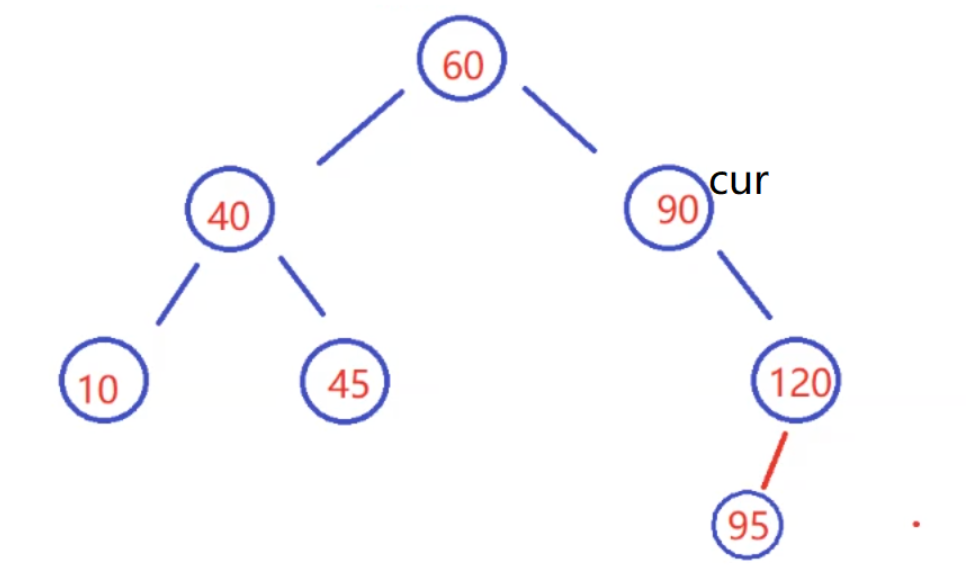
如果要删除的节点是下图的值为90的节点

通过上面对替罪羊法的讲解,我们知道我们要先找到右子树的最左边的节点,即找到了95这个节点 ,然后让95覆盖掉当前要删除的90这个节点,再删除右子树最左边值为95的节点。怎么删除呢?只需要把95的右子树连接到120的左边即可。
代码实现及其讲解:首先,我们要找到要删除的节点,找到节点后再通过方法进行删除(查找的方法可以类比插入,因为它也需要记录被删除节点的父亲节点)。
public void remove(int val){
TreeNode cur = root;
TreeNode parent = null;
while(cur != null){
if(cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
}else{//说明找到了要删除的节点
removeNode(parent,cur);
return;
}
}
}下面是删除的方法,需要分情况讨论:
情况1:cur.left == null
情况1.1:cur是root
情况如图所示:
此时只需要让root = root.right即可。
情况1.2:cur不是root,cur是parent.left
情况如图所示,直接让cur.right = parent.left即可。

情况1.3:cur不是root,cur是parent.right
如下图,只需要让cur.right = parent.right即可
 情况2:cur.right == null
情况2:cur.right == null
情况2.1:cur是root
直接让root = cur.left即可
情况2.2:cur不是root,cur是parent.left
让parent.left = cur.left。
情况2.3:cur不是root,cur是parent.right
parent.right = cur.left
情况3:cur.left != null && cur.right != null
使用上面所讲的替罪羊法解决。这里不做过多赘述。
代码实现如下:
private void removeNode(TreeNode parent,TreeNode cur){
if(cur.left == null){//被删节点的左边为空
if(cur == root){
root =cur.right;
} else if (cur == parent.left) {
parent.left = cur.right;
}else{
parent.right = cur.right;
}
} else if (cur.right == null) {//被删节点的右边为空
if(cur == root){
root =cur.left;
} else if (cur == parent.left) {
parent.left = cur.left;
}else{
parent.right = cur.left;
}
}else{//被删节点的左右两边都不为空
//可以去找左子树的最右边的元素,也可以找右子树最左边的元素,
// 对cur进行替换,
// 然后删除掉右子树最左边或者左子树最右边的元素
TreeNode target = cur.right;
TreeNode targetParent = cur;
while(target.left != null){
targetParent = target;
target = target.left;
}
cur.val = target.val;
//右子树最左边说明左边没有元素了
if(target == targetParent.left){
targetParent.left = target.right;
}else{//没进入循环的情况
targetParent.right = target.right;
}
}
}1.5 性能分析

2、搜索
2.1 概念及场景
上述排序比较适合静态类型的查找,即一般不会对区间进行插入和删除操作了,而现实中的查找比如:
2.2 模型
3、Map的使用
Map的官方文档:Map 的官方文档
3.1 关于Map的说明
3.2 关于Map.Entry<K, V>的说明

注意:Map.Entry<K,V>并没有提供设置Key的方法
3.3 Map 的常用方法说明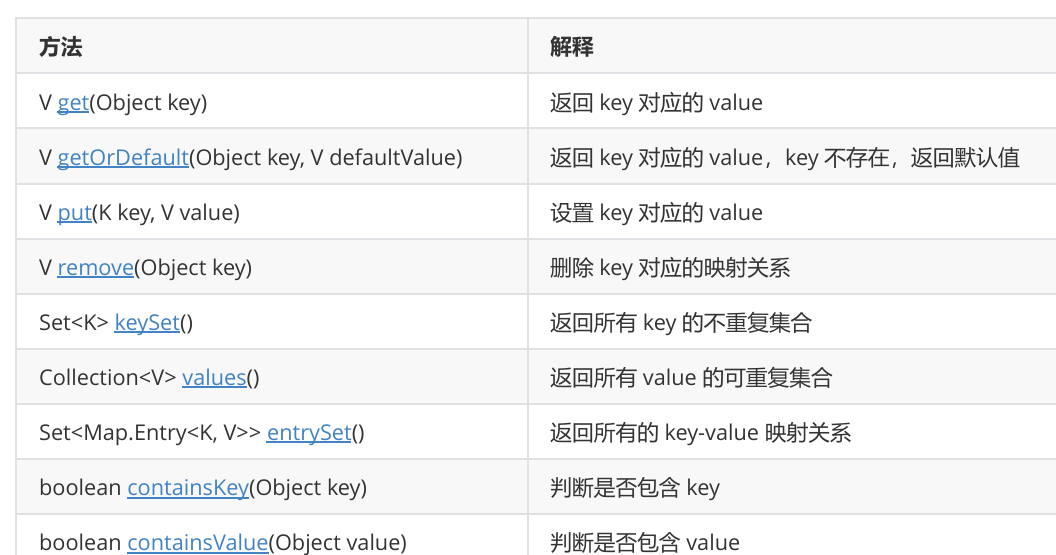
注意:
6. Map中键值对的Key不能直接修改,value可以修改,如果要修改key,只能先将该key删除掉,然后再来进行重新插入。
7. TreeMap和HashMap的区别:
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








