栈和队列 1-优快云博客

本文链接：https://blog.youkuaiyun.com/CxK6666667/article/details/145913982

1、栈

1.1 概念

栈是一种特殊的线性表，它只允许在固定的一端进行插入和删除元素。进行数据的插入和和删除的一端称为栈顶，另一端称为栈底。栈遵循先进后出，后进先出（LIFO）的原则。

压栈（push）：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈（Pop）：栈的删除操作叫做出栈。出数据在栈顶。

1.2 栈的使用

1.2.1 创建栈

如下代码创建了一个整数类型的栈。

Stack<Integer> stack = new Stack<>();

1.2.2 入栈（push（））

入栈顺序为1、2、3的栈。

        //入栈顺序：1、2、3
        //3在栈顶，1在栈底
        stack.push(1);
        stack.push(2);
        stack.push(3);

1.2.3 出栈（pop（））

返回值为int，可通过int类型的返回值输出被删除的元素。

     //弹出栈顶元素（3）
        stack.pop();
    //输出并弹出栈顶元素2
        System.out.println(stack.pop());

1.2.4 获取栈顶元素（peek（)）

获取栈顶元素的返回值为int，可通过int类型的返回值接收并输出，与pop（）不同的是，它只获取元素的值但不进行删除。

  System.out.println(stack.peek());//获取栈顶元素但不删除

1.2.5 获取栈的长度（size()）

返回值为int。

 System.out.println(stack.size());//获取栈的长度

1.2.6 判断栈是否为空(empty())

返回值为boolean。

        System.out.println(stack.empty());//判断栈是否为空

完整代码：

        Stack<Integer> stack = new Stack<>();
        stack.push(12);
        stack.push(23);
        stack.push(34);
        System.out.println(stack.pop());//删除    出栈
        System.out.println(stack.peek());//获取栈顶元素但不删除
        System.out.println(stack.size());//获取栈的长度
        System.out.println(stack.empty());//判断栈是否为空

1.3 栈的模拟实现

接下来，我们来模拟实现一个栈，ctrl+鼠标点击栈可以进入栈的底层，可以看到栈是继承了Vector这个类的。

再次进入Vector这个类里面，可以看见底层有一个数组。

1.3.1 成员变量和构造方法

由前面的分析所知，栈的底层是一个数组，因此，它与顺序表大同小异，代码如下：

     //int类型的数组
    private int[] elem;
     //有效数组的长度
    private int Usedsize;
    //默认长度为10
    private static final int DEFAULT_CAPACITY = 10;
    //创建一个默认长度的数组
    public MyStack() {
        this.elem = new int[DEFAULT_CAPACITY];//elem.length
    }

1.3.2 push( )

压栈操作：需要先判断是否栈满，如果栈满则先需要扩容再放入元素，如果栈不满则直接在Usesize处放入元素，再让usedSize++。

 //判断栈是否已满
 public boolean is_Full(){
        if(Usedsize == elem.length){
            return true;
        }
        return false;
    }
    public void push(int val){
        if(is_Full()){
            //栈满进行扩容
            Arrays.copyOf(this.elem,2*elem.length);
        }
            //在Usesize处放入元素
        elem[Usedsize] = val;
            //Usedsize++
        Usedsize++;
    }

1.3.3 isEmpty( )

  public boolean isEmpty(){
        return Usedsize == 0;
    }

1.3.4 pop( )

与ArrayList的remove（）元素不断往前覆盖不同，pop（）只需要弹出栈顶的元素，它只需要记录下原来最后一个元素的下标,然后再让Usesize--，最后返回原来最后一个元素的值。

 public int pop(){
        //判断栈是否为空
        if(isEmpty()){
            throw new NullStackException("栈中没有元素");
        }
        //记录下原来的最后一个元素的下标
        int beforesize = Usedsize - 1;
        Usedsize--;
        return elem[beforesize];
    }

1.3.5 peek( )

与pop方法大同小异，但是它不需要删除，因此，没有必要记录原来的最后一个元素。

    public int peek(){
        if(isEmpty()){
            throw new NullStackException("栈中没有元素");
        }
        return elem[Usedsize-1];
    }

完整代码：

public class MyStack {
    private int[] elem;
    private int Usedsize;

    private static final int DEFAULT_CAPACITY = 10;

    public MyStack() {
        this.elem = new int[DEFAULT_CAPACITY];//elem.length
    }
    public boolean is_Full(){
        if(Usedsize == elem.length){
            return true;
        }
        return false;
    }
    public void push(int val){
        if(is_Full()){
            Arrays.copyOf(this.elem,2*elem.length);
        }
        elem[Usedsize] = val;
        Usedsize++;
    }
    public boolean isEmpty(){
        return Usedsize == 0;
    }
    public int pop(){
        if(isEmpty()){
            throw new NullStackException("栈中没有元素");
        }
        int beforesize = Usedsize - 1;
        Usedsize--;
        return elem[beforesize];
    }
    public int peek(){
        if(isEmpty()){
            throw new NullStackException("栈中没有元素");
        }
        return elem[Usedsize-1];
    }
}

测试：

1.4 面试题

1.4.1 元素的出栈序列

这类题目只需牢记进出栈的规则（先进后出，后进先出）即可，因为2比1后进栈，所以，如果出现了2后的数字，2必须比1先出栈，因此本题选：C。

本题要求：依次入栈，依次出栈。就是把入栈的顺序倒过来，选择：B。

1.4.2 将递归转变为循环

如：逆序打印链表

递归实现：


public void reservePrintList(ListNode head) {  
     if(null != head) {
        reservePrintList(head.next);
        System.out.print(head.val + " ");
    }
}

其实这里面的原理与栈相同，就相当于申请了一个栈，将结点放入栈中，然后不断地出栈。

代码如下：

  //使用栈对链表进行逆置打印
    public void reversePrintmySinglelist(){
        //创建一个栈
        Stack<ListNode> stack = new Stack<>();
        //遍历链表
        ListNode cur = head;
        while(cur != null){
            //将每个节点入栈
            stack.push(cur);
            cur = cur.next;
        }
            //出栈并输出
        while(!stack.isEmpty()) {
            System.out.println(stack.pop().val);
        }
    }

1.4.3 20. 有效的括号 - 力扣（LeetCode）

分析：题意：

提出问题：本题为什么要使用栈来解决问题？

栈的插入和输出的时间复杂度都是O(1)，对于这个题更合适。

括号不匹配的四种情况：

解题思路：创建一个字符类型栈，通过字符串的charAt（）方法得到字符ch，把左括号放入栈中，将栈中的括号（这里必须保证栈不为空，否则说明先进来的是右括号或者多出一个右括号）与最近的右括号进行比较（左括号为栈顶元素，右括号为ch），比较成功就出栈，不成功就返回false。在比较完后还需要判断栈是否为空，如果栈不为空，说明多出一个左括号，返回false。图解如下：

完整代码：

class Solution {
    public boolean isValid(String s) {
     //分析：为什么要用栈？
        //栈的插入和删除时间复杂度是O（1），对于这个题更合适
        Stack<Character> stack = new Stack<>();
        for(int i = 0;i < s.length();i++){
            char ch = s.charAt(i);
            //进来的一定是括号
            if(ch == '(' ||ch == '['||ch =='{'){
                stack.push(ch);
            }else{
                //进来的先是右括号
                if(stack.empty()){
                    return false;
                }
                //此时左括号是栈顶元素，右括号是ch
                char top = stack.peek();
                if(top == '(' && ch == ')'
                        || top == '[' && ch == ']'
                        || top == '{' && ch =='}'){
                    stack.pop();
                }else{//左括号和右括号不匹配
                    return false;
                }
            }
        }
        if(!stack.empty()){
            return false;
        }
        return true;
    }
}

1.4.4 150. 逆波兰表达式求值 - 力扣（LeetCode）

在解决这道题前我们需要先了解：什么是中缀表达式，什么是后缀表达式？

中缀表达式其实就是我们平时所写的式子，例如：（1+2）*5，而我们平时写的式子如果丢给计算机进行计算就会转变为后缀表达式：12*5+。

下面我们通过例子来感受下它们是如何转变的：

中缀表达式： a + b * c + (d * e + f) * g

其后缀表达式为：a b c * + d e * f + g * +

1、先把式子按照先乘除后加减上括号

2、把对应的运算符放到对应括号的外面

3、把括号去掉

那么计算机是如何计算的呢？

假设 a = 1， b = 2， c = 3， d = 4， e = 5， f = 6， g = 7，则a + b * c + (d * e + f) * g 即计算 1 + 2 * 3 + (4 * 5 + 6) * 7

计算机会先将前缀表达式转换为后缀表达式：1 + 2 * 3 + (4 * 5 + 6) * 7 >> 1 2 3 *4 5 * 6 + 7 + *，定义一个i下标向后遍历后缀表达式，将数字放入栈中，当遍历到符号时就弹出栈顶的两个元素，第一个弹出的为右操作数，第二个弹出的为左操作数，计算完后放回栈中，重复上述过程。

图解如下：

代码如下：

 public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
        for(int i = 0;i < tokens.length;i++){
            String s = tokens[i];
            if(!isOperation(s)){
                //数字字符
                stack.push(Integer.valueOf(s));
            }else{
                //+ - * /之一
                //n1比n2先入栈，因此后出
                int n2 = stack.pop();
                int n1 = stack.pop();
                switch(s){
                    case "+":
                        stack.push(n1+n2);
                        break;
                    case "-":
                        stack.push(n1-n2);
                        break;
                    case "*":
                        stack.push(n1*n2);
                        break;
                    case "/":
                        stack.push(n1/n2);
                        break;
                }
            }
        }
        return stack.pop();
    }
    //判断是否为"+""-""*""/"
    private boolean isOperation(String s){
        if(s.equals("+")||s.equals("-")||s.equals("*")||s.equals("/")){
            return true;
        }
        return false;
    }

1.4.5 栈的压入、弹出序列_牛客题霸_牛客网 (nowcoder.com)

分析:本题需要写一个程序判断popV[ ]能否是栈pushV[ ]的出栈顺序（1.4.1类型的题目）。

解题思路：假设如图，是一个pushV[ ]和popV[ ]，按pushV[ ]入栈，能否按popV[ ]出栈。

可以用i、j分别遍历这两个数组。

遍历pushV[ ] 的时候将元素放入栈中，然后进行判断如果栈顶的元素与当前popV中的元素进行比较如果不相同，则将pushV[ ]中的元素继续入栈；如果相同则开始出栈，同时j++进行下次判断。（重复上述过程）。

开始出栈：

这里的栈顶元素3与PopV[ j ]的值不同，因此我们需要把5入栈再与popV[j]进行比较，然后继续出栈即可。

完整代码：

    //判断是否为栈的弹出序列
    public boolean IsPopOrder (int[] pushV, int[] popV) {
        //1、遍历pushV数组每次拿到一个数据就放到栈中
        Stack<Integer> stack = new Stack<>();
        int j = 0;
        for(int i = 0;i < pushV.length;i++){
            stack.push(pushV[i]);
            while(!stack.empty() && j < popV.length && stack.peek() == popV[j]){
                stack.pop();
                j++;
            }
        }
        return stack.empty();
    }

1.4.6 155. 最小栈 - 力扣（LeetCode）

分析：

由题意知：要在常数时间内检索到最小元素，而一个栈的情况下至少也需要O（n）的时间复杂度，由此可以想到：我们需要使用两个栈，一个栈为正常栈，另一个栈为最小栈（存储栈中的最小值）。

解题思路：入栈：stack（正常栈）入所有元素，将每个入栈元素与最小栈（minStack）的栈顶元素进行比较，如果小于等于或者栈为空就要进栈。出栈：stack正常出栈，将出栈的元素与最小栈的栈顶元素比较，如果相等则需要出栈。如：要将 -3、1、9、3入栈，并要求得到它的最小值

放入第一个元素： 1 > -3直接入栈：

-9 <-3，需要入最小栈：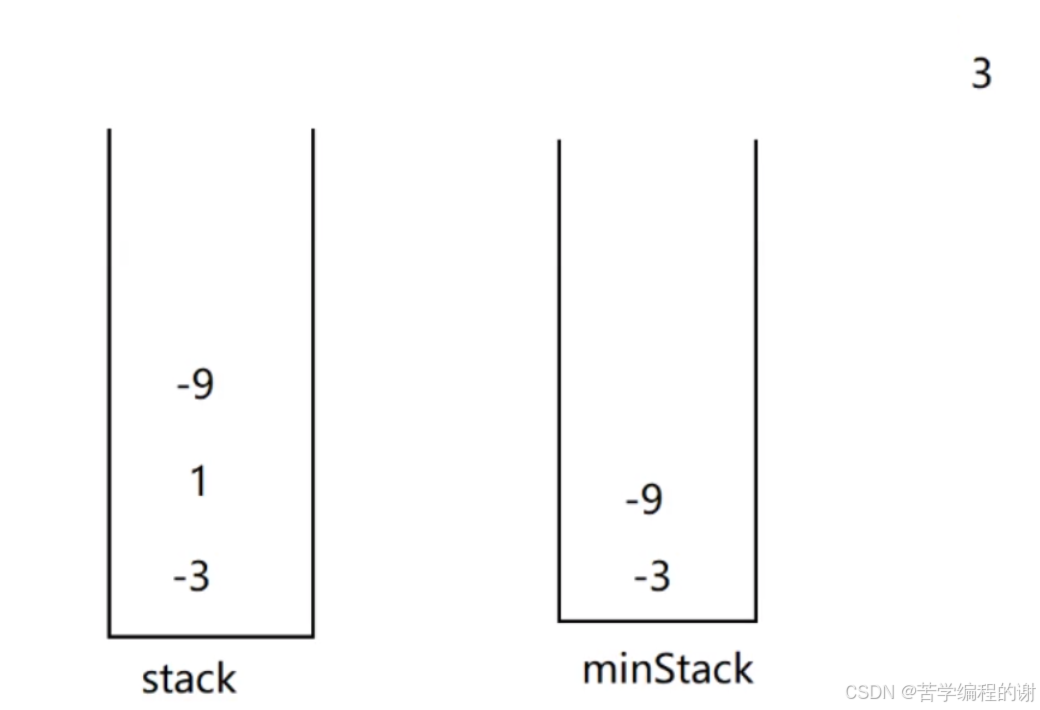

3>-9直接放入即可：出栈：

正常出完3后，发现要出的元素-9与最小栈的栈顶元素相同，因此一起出栈。

完整代码：

class MinStack {
 //入栈
 //stack入所有元素
 //将入栈元素与minStack栈顶元素比较，如果小于等于或者栈为空则入栈
 //出栈
 //stack正常出，将出栈元素与minStack的栈顶元素比较，如果相同就出栈
 Stack<Integer> stack;
 Stack<Integer> minStack;
    public MinStack() {
        stack = new Stack<>();
        minStack = new Stack<>();
    }
    
    public void push(int val) {
        stack.push(val);
        if(minStack.empty()){
            minStack.push(val);
        }else{
            if(minStack.peek() >= val){
                minStack.push(val);
            }
        }
    }
    public void pop() {
        if(!stack.empty()){
            int ret = stack.pop();
            if(ret == minStack.peek()){
                minStack.pop();
            }
        }
    }
    //获取正常栈栈顶元素    
    public int top() {
        if(stack.empty()){
            return -1;
        }
        return stack.peek();
    }
    //获取最小栈栈顶元素
    public int getMin() {
        if(minStack.empty()){
            return -1;
        }
        return minStack.peek();
    }
}

1.5 栈、虚拟机栈、栈帧的区别

1、栈：一种数据结构，遵循后进先出的原则，有入栈(push) 和出栈(pop)操作，是一种通用的概念，并不拘束于某种具体的编程语言或者虚拟机。

2、虚拟机栈：是 Java 虚拟机（JVM）运行时数据区的一部分，是 Java 程序执行的核心区域之一。它是 Java 虚拟机为每个线程创建的私有内存区域，主要用于支持 Java 方法的执行。每个线程在执行 Java 方法时，都会在虚拟机栈中创建一个或多个栈帧来存储方法的相关信息。每个线程都会有其独立的虚拟机栈。

3、栈帧：是虚拟机栈中的基本元素，是用于支持虚拟机进行方法调用和方法执行的数据结构。每一个方法从调用开始到执行完成的过程，都对应着一个栈帧在虚拟机栈中的入栈到出栈的过程。它就像是一个专门为方法执行准备的 “小房间”，里面存放着方法执行所需的各种数据，如局部变量、操作数栈、方法出口等信息。