经典算法之：递归（以斐波那契数列问题看待递归）

  在世界的万事万物中，总有些东西要一直重复做下去。比如说你一个月的1号早上7点跑步，2号早上7点跳绳，3号早上7点打羽毛球…如此做下去，做30天(假设每一个月都有30天)，然后下个月在如此做重复的事情。这就是循环。

  在了解递归之前，我们先了解下一迭代

一、迭代：

  迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值。

例如：一个for循环的一次操作就是一次迭代.

for(int i =0; i <= 100; i++){
	Sysout.out.prient("这是一次迭代");
	}

迭代的循环过程如下：

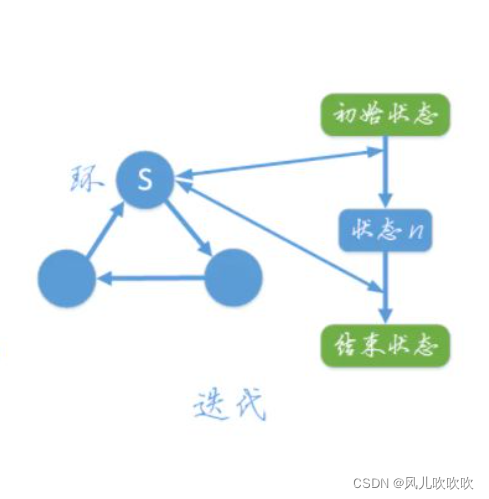
  由上图可清楚的得到，一次迭代就是一次循环，所以迭代是一个环结构。迭代从初始状态开始，每次迭代都遍历这个环，并更新状态，多次迭代直到到达结束状态。

但是对于一个大型且复杂的问题来说，迭代就显得很拖累。因为要循环的环很大很大。于是，就有了递归。接下来我们说说递归。

二、递归

1.递归的定义

   递归常被用来描述以自相似方法重复事物的过程，在数学和计算机科学中，指的是在函数定义中使用函数自身的方法。（A调用A）

简单来说：就是在运行过程中调用自己。

2.递归的条件

  构成递归也是有条件的，其条件如下:

1. 子问题须与原始问题为同样的事。
2. 不能无限制地调用本身，须有个出口，化简为非递归状况处理。

3.递归的意义

  在解决某些循环问题时候，简单的循环已经无法解决问题。如果要解决问题，就要牺牲很大的时间及成本。因此，使用递归就能直接给出一个自然、直接、简单的解决方式。它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

4.递归的过程

  上图可明确的显示了迭代是一个环结构，在每次迭代都遍历这个环。而递归自己调用自己的过程就已经分成了一个个节点，一个节点在分为另一个节点。就逐渐演示出了一个“树”。
  所以，递归是一个树结构。从字面可以其理解为重复“递推”和“回归”的过程，当“递推”到达底部时就会开始“回归”，其过程相当于树的深度优先遍历。

递归的结构如下：

例如，对于问题：求6！来说，其递归的过程如下：

注意：递归是自己调用自己。在Java中，函数是基于栈来运行的，所以，递归的过程中会增加栈的开销，在调用过程中可能会报出：StackOverflowError(栈溢出异常)。

三、斐波那契数列

         斐波那契数列是一个经典的递归问题

1.斐波那契数列的定义

  有这样一个数列：1、1、2、3、5、8、13、21、34、……这个数列从第3项开始，每一项都等于前两项之和。这就是斐波那契数列，也称：黄金分割数列。

2.使用递归的思想计算斐波那契数列

首先，将斐波那契数列放入数组，如下图：

由数列的定义可的从0和1开始，之后每个数都是序列中前两个的和。因此可以写为：

fib(0) = 0;
fib(1) = 1;
fib(index)=fib(index-2)+fib(index-1);(index >=2)

这是递归的思想，每一个值都是前面两个之和，将其递归下去。简单理解就是每一个下标的数都做着同样的事情。重复下去。

那么，总不能让其一直无限的循环下去。要进行递归，就要满足其递归的条件。已经满足其中之一了，那么就要满足边界条件。

由数租可知，当下标>=2时才开始前2个加前1个

所以，其的边界条件为:

if(index == 0){
	return 0;
}else if(index == 1){
	return 1 ;
}else{
	return fib(index-2)+fib(index-1);
}

因此，就可以计算出给出第n个斐波那契数列的值。

3.代码实现

public class Fibonacci {
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        System.out.println("请输入你想要求的数的下标:" );
        int index = input.nextInt();

        System.out.println("斐波那契数列下标"+index+"的值为："+fib(index));
    }

    private static long fib(int index) {
        if(index == 0){
            return 0;
        }else if(index == 1){
            return 1 ;
        }else{
            return fib(index-2)+fib(index-1);
        }
    }
}

运行结果：
请输入你想要求的数的下标:
6
斐波那契数列下标6的值为：8