判断一个树是不是另一个树的子树

最主要的思想就是递归！！！

一般对于树的解决问题都是递归

我们这里就写成A树和B树   那么题意也就变成了  B树是A树的子树

子树也就是 B树是A树中的一部分    那么首先就要判断这两部分是不是相等

递归

首先比较根节点，如果根节点相等并且根节点的所有字节点都相等，那么我们就接着向下递归

这里需要仔细考虑一种情况   子树  那么只要是一部分就行  不用非得是下面完全相同

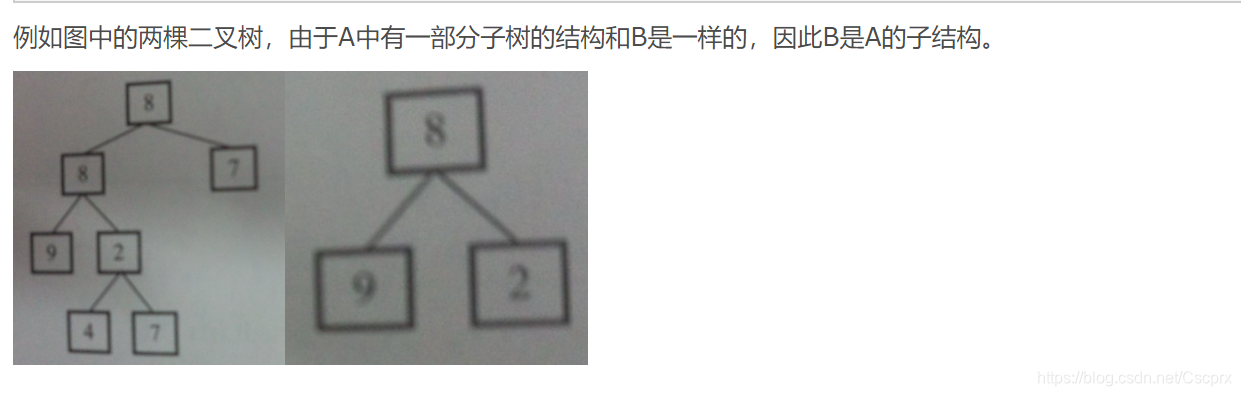
例如这个例子

所以代码如下

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    public boolean HasSubtree(TreeNode root1,TreeNode root2) {
        if(root1 == null||root2 == null)
            return false;
        if(equals(root1,root2))
            return true;
        else return HasSubtree(root1.left,root2)||HasSubtree(root1.right,root2);
    }
    boolean equals(TreeNode t1,TreeNode t2){
        if(t2 == null) // 这里尤其要注意
            return true;
        if(t1 == null)
            return false;
        return t1.val == t2.val && equals(t1.left,t2.left) && equals(t1.right,t2.right);
    }
}

代码中注意：这里的顺序不能变  也就是说我们必须要先判断子树是不是空  如果B树是空而A不是，那么这种情况是存在的

如果A树是空  B树不是  那么显然不成立