博客重点围绕神经网络原理展开，包括分层化解复杂度、梯度下降进阶理解等。还提及链式求导、正向与反向传播等概念，以及随机初始化、偏导数对拍程序等其他问题。此外，给出课程用到的公式，并分享了练习中的经验，如costFunction编写、反向传播实现等。
神经网络
摘要
重点在理解神经网络的原理，必须以上周神经网络模型为基础，这一周主要都是讲讲对于原理的理解。
ps. 神经网络这一周的课程折腾了好几天，总算是看明白了。
本周不管是原理还是练习都挺难做的，原理理解起来东西很多，这一节课讲得不够清楚，但我很理解，本身就很难讲明白。其实理解之后还是比较直观的。本来模型就挺复杂，各种下标弄到熟也麻烦。我是如此处理的，看一遍课程，做一部分练习，下标就基本熟了。然后看油管上3b2b的视频，多看两遍吧，讲得真好，这么繁杂的东西，理解原理，再看一遍coursera视频，再完成练习。
神经网络原理
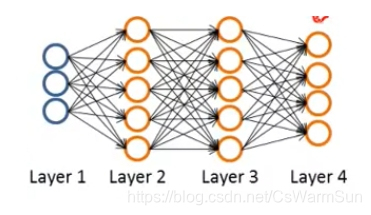
分层化解复杂度
这个要见上周内容，这个涉及到神经网络的模型结构涉及，其实说白了原理很简单，我们解决很多任务量巨大的问题的时候，使用的就是分层的思想，复杂度下降得非常快。
梯度下降进阶理解
我觉得这个实在是太神奇了，三维的时候，我们可以想象为下山最快的方式，高纬度其实也一样，只不过上述想象不再管用。我们可以理解为某函数对某个变量的敏感程度，也就是这个变量最有性价比的下降方向。
思想——关于神经网络本质的思考
神经网络的思想不难，关键难点在于如何用损失函数J如何调节各权重。理解了梯度下降，虽然经过分层，以及sigmoid函数映射，但J本质上就是关于所有θ的函数，θ也就是权重，调节权重，使得J取得最小值，如何调节最有性价比？当然就是梯度下降。J对各个θ的偏导数就是对于各个θ的敏感度描述。——神经网络模型其实也就是J(θ1,θ2,θ3…)一个超长函数梯度下降求最小值。
其实说白了和逻辑回归没啥区别，只不过，theta实在太多了，为了效率，才有了神经网络的分层模型。问题在于，通常参数都会非常非常多，所以神经网络模型很有效，收敛得非常快。
链式求导
因为分层，导致求每个参数θ的导数并不是那么容易的一件事，何况中间还有一个sigmoid函数。特别是实现的过程，会有很多很多的中间变量，但本质上就是多元函数的链式法则求偏导。
我觉得这个真该好好看看3b2b的视频。
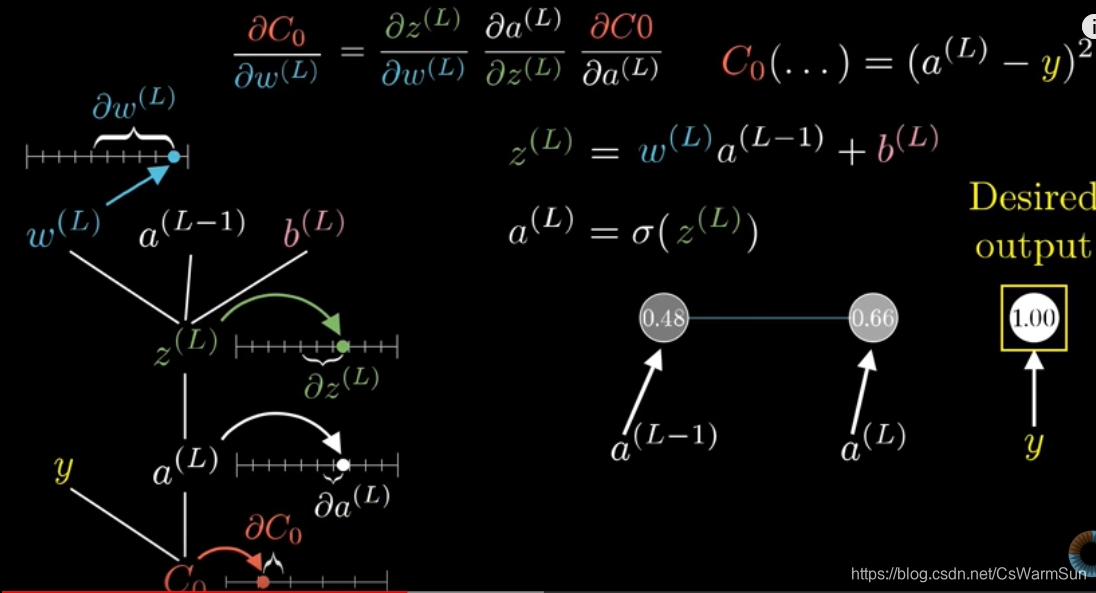
神经网络中的概念
正向传播&&反向传播
看起来很高级，其实正向传播是计算损失函数的方向——从左到右。
而反向传播，则是从损失函数求导各层的参数——从右到左。求导的方法就是链式法则。
动态规划
不管是从左到右的计算还是从右到左的计算，都是一层推导一层，并且引入是error——δ系列，其实应该都是前后项的递推，尤其是求导过程，动态规划，所以效率会快很多。
效率思考
从大O意义上，需要调参N * F（特征数量）* iter（迭代次数），每次调参都需要调用costFunction，这个函数，对于神经网络，需要计算J，计算delta，使用了动态规划，姑且认为是O（N）；而数值的方法，明显是N次循环，每次都需要计算J，所以是O(N*N)。尽管看上去十分简洁。
其他问题
随机初始化
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
epsilon取值推荐
ϵ
i
n
i
t
=
6
L
i
n
+
L
o
u
t
\epsilon_{i n i t}=\frac{\sqrt{6}}{\sqrt{L_{i n}+L_{o u t}}}
ϵinit=Lin+Lout6
数值化偏导数——偏导数对拍程序
提供的对拍程序非常实用。
function numgrad = computeNumericalGradient(J, theta)
% J为costFunction
numgrad = zeros(size(theta));
perturb = zeros(size(theta));
e = 1e-4;
for p = 1:numel(theta)
% Set perturbation vector
perturb(p) = e;
loss1 = J(theta - perturb);
loss2 = J(theta + perturb);
% Compute Numerical Gradient
numgrad(p) = (loss2 - loss1) / (2*e);
perturb(p) = 0;
end
end
问题：为什么这个方式会很慢？
见效率思考
如何描述结果的准确性。
diff = norm(numgrad-grad)/norm(numgrad+grad);
代码是用差的标准差除以和的标准差，如果二者非常接近，那么diff值应该非常非常小。
课程用到的公式
以下是课程用到的公式，但是，这些很难看懂，因为课程安排很乱，只是方便实现而收集的。
∂
∂
Θ
i
,
j
(
l
)
J
(
Θ
)
\frac{\partial}{\partial \Theta_{i, j}^{(l)}} J(\Theta)
∂Θi,j(l)∂J(Θ)
正向传播
z
(
j
+
1
)
=
Θ
(
j
)
a
(
j
)
z^{(j+1)}=\Theta^{(j)} a^{(j)}
z(j+1)=Θ(j)a(j)
h Θ ( x ) = a ( j + 1 ) = g ( z ( j + 1 ) ) h_{\Theta}(x)=a^{(j+1)}=g\left(z^{(j+1)}\right) hΘ(x)=a(j+1)=g(z(j+1))
实例
a
(
1
)
=
x
z
(
2
)
=
Θ
(
1
)
a
(
1
)
a
(
2
)
=
g
(
z
(
2
)
)
(
add
a
0
(
2
)
)
z
(
3
)
=
Θ
(
2
)
a
(
2
)
a
(
3
)
=
g
(
z
(
3
)
)
(
add
a
0
(
3
)
)
z
(
4
)
=
Θ
(
3
)
a
(
3
)
a
(
4
)
=
h
Θ
(
x
)
=
g
(
z
(
4
)
)
\begin{aligned} a^{(1)} &=x \\ z^{(2)} &=\Theta^{(1)} a^{(1)} \\ a^{(2)} &=g\left(z^{(2)}\right)\left(\operatorname{add} a_{0}^{(2)}\right) \\ z^{(3)} &=\Theta^{(2)} a^{(2)} \\ a^{(3)} &=g\left(z^{(3)}\right)\left(\operatorname{add} a_{0}^{(3)}\right) \\ z^{(4)} &=\Theta^{(3)} a^{(3)} \\ a^{(4)} &=h_{\Theta}(x)=g\left(z^{(4)}\right) \end{aligned}
a(1)z(2)a(2)z(3)a(3)z(4)a(4)=x=Θ(1)a(1)=g(z(2))(adda0(2))=Θ(2)a(2)=g(z(3))(adda0(3))=Θ(3)a(3)=hΘ(x)=g(z(4))
损失函数
单个损失其实是（忽略正则项）
cost
(
i
)
=
y
(
i
)
log
h
Θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
log
h
Θ
(
x
(
i
)
)
\operatorname{cost}(\mathrm{i})=y^{(i)} \log h_{\Theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log h_{\Theta}\left(x^{(i)}\right)
cost(i)=y(i)loghΘ(x(i))+(1−y(i))loghΘ(x(i))
损失均值
J
(
Θ
)
=
−
1
m
∑
i
=
1
m
∑
k
=
1
K
[
y
k
(
i
)
log
(
(
h
Θ
(
x
(
i
)
)
)
k
)
+
(
1
−
y
k
(
i
)
)
log
(
1
−
(
h
Θ
(
x
(
i
)
)
)
k
)
]
+
λ
2
m
∑
l
=
1
L
−
1
∑
i
=
1
s
l
+
1
∑
j
=
1
s
l
+
1
(
Θ
j
,
i
(
l
)
)
2
J(\Theta)=-\frac{1}{m} \sum_{i=1}^{m} \sum_{k=1}^{K}\left[y_{k}^{(i)} \log \left(\left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}\right)+\left(1-y_{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}\right)\right]+\frac{\lambda}{2 m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_{l+1}} \sum_{j=1}^{s_{l+1}}\left(\Theta_{j, i}^{(l)}\right)^{2}
J(Θ)=−m1i=1∑mk=1∑K[yk(i)log((hΘ(x(i)))k)+(1−yk(i))log(1−(hΘ(x(i)))k)]+2mλl=1∑L−1i=1∑sl+1j=1∑sl+1(Θj,i(l))2
delta
这东西引入是为了求偏导数D的，以下为实例中的公式。
δ
(
4
)
=
a
(
4
)
−
y
\delta^{(4)}=a^{(4)}-y
δ(4)=a(4)−y
δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) . ∗ g ′ ( z ( 3 ) ) δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) . ∗ g ′ ( z ( 2 ) ) \begin{aligned} \delta^{(3)} &=\left(\Theta^{(3)}\right)^{T} \delta^{(4)} .* g^{\prime}\left(z^{(3)}\right) \\ \delta^{(2)} &=\left(\Theta^{(2)}\right)^{T} \delta^{(3)} .* g^{\prime}\left(z^{(2)}\right) \end{aligned} δ(3)δ(2)=(Θ(3))Tδ(4).∗g′(z(3))=(Θ(2))Tδ(3).∗g′(z(2))
最后一项的求法
g
′
(
z
(
l
)
)
=
a
(
l
)
⋅
∗
(
1
−
a
(
l
)
)
g^{\prime}\left(z^{(l)}\right)=a^{(l)} \cdot *\left(1-a^{(l)}\right)
g′(z(l))=a(l)⋅∗(1−a(l))
使用delta求D，下面公式表示和后面一项有关，单个偏导，其实模糊的地方就是这里，求导应该非常复杂，多层求导。
∂
∂
Θ
i
j
(
l
)
J
(
Θ
)
=
a
j
(
l
)
δ
i
(
l
+
1
)
\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=a_{j}^{(l)} \delta_{i}^{(l+1)}
∂Θij(l)∂J(Θ)=aj(l)δi(l+1)
中间变量DELTA，没啥实际含义，下面两公式，上面为单个值，下为vector
△
i
j
(
l
)
:
=
Δ
i
j
(
l
)
+
a
j
(
l
)
δ
i
(
l
+
1
)
\triangle_{i j}^{(l)} :=\Delta_{i j}^{(l)}+a_{j}^{(l)} \delta_{i}^{(l+1)}
△ij(l):=Δij(l)+aj(l)δi(l+1)
Δ ( l ) : = Δ ( l ) + δ ( l + 1 ) ( a ( l ) ) T \Delta^{(l)} :=\Delta^{(l)}+\delta^{(l+1)}\left(a^{(l)}\right)^{T} Δ(l):=Δ(l)+δ(l+1)(a(l))T
D表示最终偏导项，这个应该叫做，偏导均值
∂
∂
Θ
i
j
(
l
)
J
(
Θ
)
=
D
i
j
(
l
)
\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=D_{i j}^{(l)}
∂Θij(l)∂J(Θ)=Dij(l)
最后把每个输出的所有D值加起来，求均值。
D
i
j
(
l
)
:
=
1
m
△
i
j
(
l
)
+
λ
Θ
i
j
(
l
)
if
j
≠
0
D
i
j
(
l
)
:
=
1
m
Δ
i
j
(
l
)
if
j
=
0
\begin{array}{ll}{D_{i j}^{(l)} :} & {=\frac{1}{m} \triangle_{i j}^{(l)}+\lambda \Theta_{i j}^{(l)} \text { if } j \neq 0} \\ {D_{i j}^{(l)}} & { :=\frac{1}{m} \Delta_{i j}^{(l)}} & {\text { if } j=0}\end{array}
Dij(l):Dij(l)=m1△ij(l)+λΘij(l) if j̸=0:=m1Δij(l) if j=0
回过头来看，δ有什么用，其实这个是求导的中间变量
δ
j
(
l
)
=
∂
∂
z
j
(
l
)
cost
(
i
)
\delta_{j}^{(l)}=\frac{\partial}{\partial z_{j}^{(l)}} \operatorname{cost}(\mathrm{i})
δj(l)=∂zj(l)∂cost(i)
练习
- costFunction，不好写，用不了矩阵运算，然后就是Regularized 的 costFunction
反向传播
- gradientSigmoid，sigmoid的梯度下降
- 随机初始化
- 反向传播的实现，单组数据处理，用大循环解决。非常麻烦的一个实验，首先弄清楚了神经网络的原理，课程讲得比较一般，然后写出程序老是出问题，是一个括号没注意，浪费了特别长的时间。
- 学会偏导数对拍程序，利用数值的方法计算，对比二者差距
- 正则化神经网络
- 显示隐藏层为图片，重构图片的代码很值得学习
- 体会神经网络的强大，过拟情况下，可以到达100%的拟合。人脸识别，就这个技术吧
代码见github https://github.com/KDL-in/MachineLearningOnCoursera
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
