神经网络学习（三）

神经网络(三)

SVM

Support Vector Machine

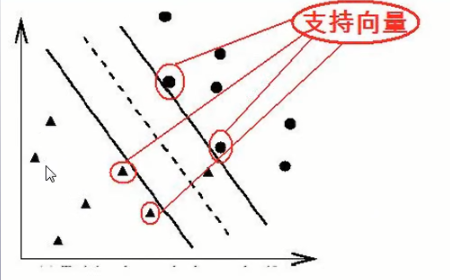
SVM 的主要思想是建立一个超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化

优点

• 通用性
• 鲁棒性
• 有效性
• 计算简单
• 理论上完善

用SVM做分类问题处理的流程：

• 选定训练集和测试集>> 规范化>>特征提取>>

• 利用训练集训练分类器得到model>>

• 利用model对测试集进行测试

• 分类器性能评估

  从UCI上下载数据集load wine_SVM.txt;

  data = [wine(:,1), wine(:,2)];
  
  groups = ismember(wine_labels,1); 
  
  [train, test] = crossvalind('holdOut',groups); % not familiar with crossvalind? help... help...
  
  train_wine = data(train,:);
  train_wine_labels = groups(train,:);
  train_wine_labels = double( train_wine_labels );
  
  test_wine = data(test,:);
  test_wine_labels = groups(test,:);
  test_wine_labels = double( test_wine_labels );
  
  model = svmtrain(train_wine_labels, train_wine, '-c 1 -g 0.07');
  
  [predict_label, accuracy] = svmpredict(test_wine_labels, test_wine, model);

  画图

  [mm,mn] = size(model.SVs);
  
  figure;
  hold on;
  [m,n] = size(train_wine);
  for run = 1:m
    if train_wine_labels(run) == 1
        h1 = plot( train_wine(run,1),train_wine(run,2),'r+' );
    else
        h2 = plot( train_wine(run,1),train_wine(run,2),'g*' );
    end
    for i = 1:mm
        if model.SVs(i,1)==train_wine(run,1) && model.SVs(i,2)==train_wine(run,2)
            h3 = plot( train_wine(run,1),train_wine(run,2),'o' );
        end
    end
  end
  legend([h1,h2,h3],'1','0','Support Vectors');
  hold off;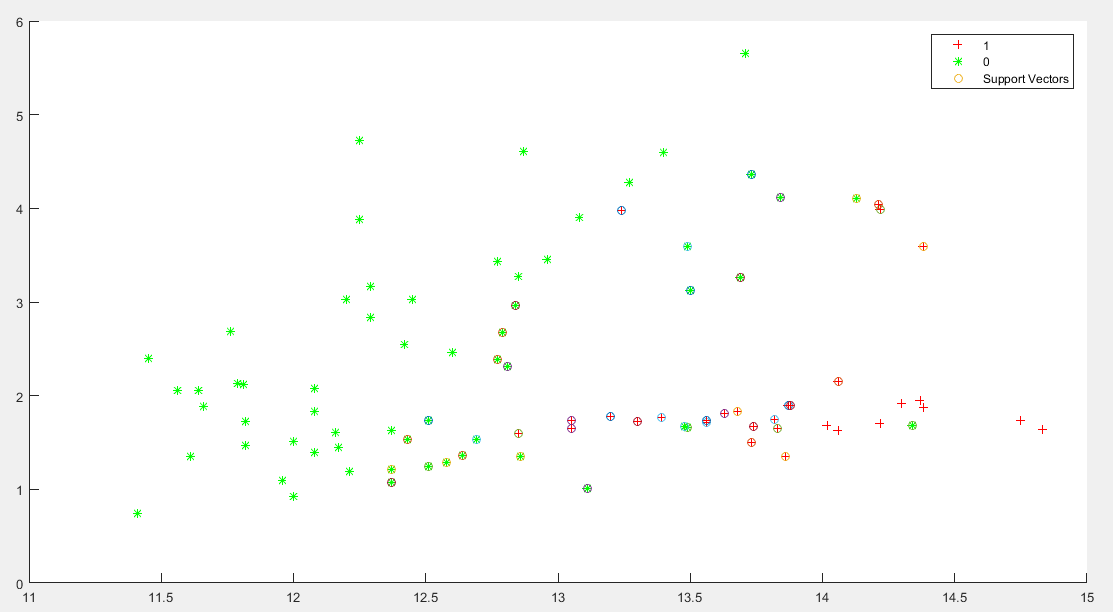

  

  此次Accuracy = 84.0909% (74/88) (classification)

  可通过

  train_wine = normalization(train_wine’,2);
  test_wine = normalization(test_wine’,2);
  train_wine = train_wine’;
  test_wine = test_wine’;

  对数据进行规范化

  如果为1 ，则把数据规范为[0,1]

  如果为2 ，则把数据规范为[-1,1]

  规范化不一定是必须的，根据数据的不同可进行不同的规范化

支持向量机方法是建立在统计学习理论的VC维理论和结构风险最校园里基础上的

• 所谓VC维是对函数类的一种度量，可以简单的理解为问题的复杂程度，VC维越高，一个问题就越复杂
• 正是因为SVM关注的是VC维

SVM解决非线性的思维方式

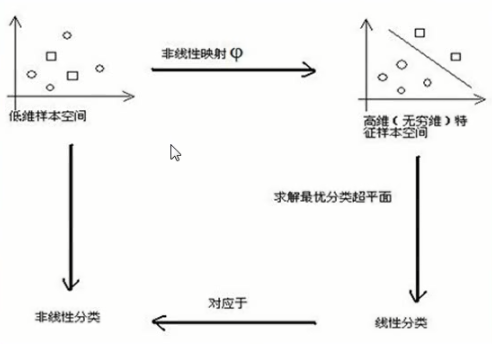
寻找最优超平面方法

• 公式

  $w*x+b=0$

• 目的

  寻找最优的分类超平面，即寻找最优的w和b，设最优的w和b为$w_0$和$b_0$,则最优的分类超平面为：

  $w_0*x+b_0 = 0$

• 获得上面的最优分类超平面，就可以用其来对测试集进行预测了

• 正反例间隔

  

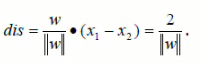
SVM的主要思想是建立一个超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化

即最优分类超平面等价于求最大间隔