分治棋盘覆盖

问题描述
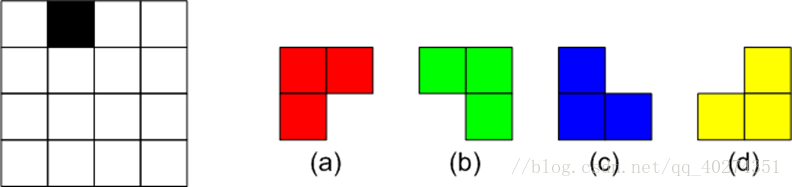
在一个2k×2k （k≥0）个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为特殊方格。显然，特殊方格在棋盘中可能出现的位置有4k种，因而有4k种不同的棋盘，图4.10(a)所示是k=2时16种棋盘中的一个。棋盘覆盖问题（chess cover problem）要求用图4.10(b)所示的4种不同形状的L型骨牌覆盖给定棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

实现：

1. 每次都对分割后的四个小方块进行判断，判断特殊方格是否在里面。
2. 这里的判断的方法是每次先记录下整个大方块的左上角topLeftConer
   方格的行列坐标
3. 然后再与特殊方格坐标进行比较，就可以知道特殊方格是否在该块中。
4. 如果特殊方块在里面，直接递归下去求即可
5. 如果不在，这根据分割的四个方块的不同位置，把右下角、左下角、右上角或者左上角的方格标记为特殊方块，然后继续递归。

---

注意： 在递归函数里，还要有一个变量s来记录边的方格数，每次对方块进行划分时，边的方格数都会减半，这个变量是为了方便判断特殊方格的位置。其次还要有一个变nCount来记录L型骨牌的数量。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int nCount = 0,t=0;
int board[100][100];

// void chessBoard(int tr, int tc, int dr, int dc, int size);
void ChessBoard(int tr, int tc, int dr, int dc, int size)
{
    int s, t1; //t1表示本次覆盖所用L型骨牌的编号
    if (size == 1)
        return;                        //棋盘只有一个方格且是特殊方格
    t1 = ++t;                          // L型骨牌编号
    s = size / 2;                      // 划分棋盘
    if (dr < tr + s && dc < tc + s)    //特殊方格在左上角子棋盘中
        ChessBoard(tr, tc, dr, dc, s); //递归处理子棋盘
    else
    { //用 t1号L型骨牌覆盖右下角，再递归处理子棋盘
        board[tr + s - 1][tc + s - 1] = t1;
        ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
    }
    if (dr < tr + s && dc >= tc + s)       //特殊方格在右上角子棋盘中
        ChessBoard(tr, tc + s, dr, dc, s); //递归处理子棋盘
    else
    { //用 t1号L型骨牌覆盖左下角，再递归处理子棋盘
        board[tr + s - 1][tc + s] = t1;
        ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);
    }
    if (dr >= tr + s && dc < tc + s)       //特殊方格在左下角子棋盘中
        ChessBoard(tr + s, tc, dr, dc, s); //递归处理子棋盘
    else
    { //用 t1号L型骨牌覆盖右上角，再递归处理子棋盘
        board[tr + s][tc + s - 1] = t1;
        ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);
    }
    if (dr >= tr + s && dc >= tc + s)          //特殊方格在右下角子棋盘中
        ChessBoard(tr + s, tc + s, dr, dc, s); //递归处理子棋盘
    else
    { //用 t1号L型骨牌覆盖左上角，再递归处理子棋盘
        board[tr + s][tc + s] = t1;
        ChessBoard(tr + s, tc + s, tr + s, tc + s, s);
    }
}

int main()
{
    int size, r, c, row, col;
    memset(board, 0, sizeof(board));
    scanf("%d", &size);        //方阵大小
    scanf("%d%d", &row, &col); //特殊点，坐标从1开始
    ChessBoard(0, 0, row, col, size);
    for (r = 0; r < size; r++)
    {
        for (c = 0; c < size; c++)
        {
            printf("%2d ", board[r][c]);
        }
        printf("\n");
    }
    return 0;
}

参考链接：

1. 棋盘覆盖百度百科
2. 棋盘覆盖问题-分治法By: JoJonny

---

代码思路，编辑格式不易，大家觉得还可以可以点赞、收藏、关注一下吧！
也可以到我的个人博客参观一下，https://motongxue.gitee.io