【算法】一文带你搞懂0-1背包问题！（理论篇）

理论基础

背包问题分为以下几种：

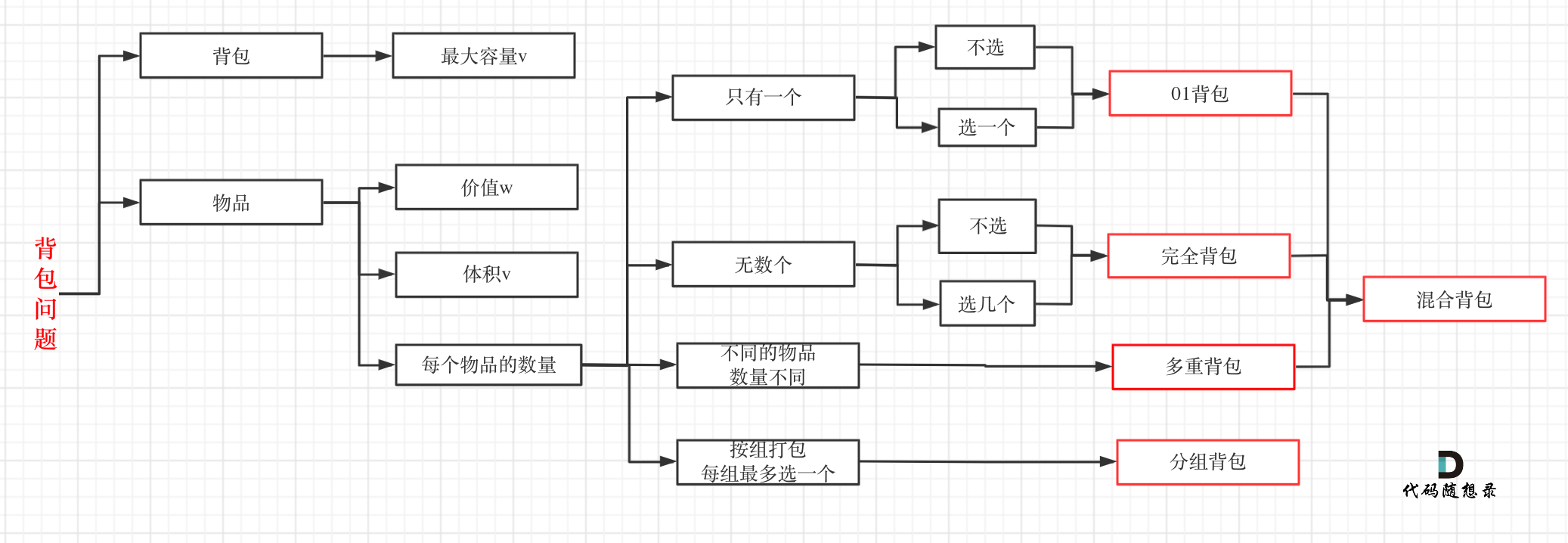
对于面试的话，掌握01背包和完全背包，就够用了。leetcode上连多重背包的题目都没有，所以题库也告诉我们，01背包和完全背包就够用了。

而完全背包又是01背包稍作变化而来，即：完全背包的物品数量是无限的。

所以背包问题的理论基础重中之重是01背包。

leetcode上没有纯01背包的问题，都是01背包应用方面的题目，也就是需要转化为01背包问题。

所以先通过纯01背包问题，把01背包原理弄清楚，后续遇到相关leetcode题目的时候，重点就是如何转化为01背包问题了。

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

这是就标准的背包问题。

暴力解法应该是怎么样的呢？

每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是，这里的n表示物品数量。

所以暴力的解法是指数级别的时间复杂度，进而才需要动态规划的解法来进行优化。

举一个例子：

背包最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

以下讲解和图示中出现的数字都是以这个例子为例。

值得注意的是，背包问题可用二维dp数组和一维dp数组两种形式解决。二维dp数组比较容易理解；而一维dp数组的写法比较直观简洁，且空间复杂度还降了一个数量级，所以一般都用一维dp数组。

二维dp数组求解

动规五部曲：

1. 确定dp数组以及下标的含义

dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

只看这个二维数组的定义，可能会有点懵，看下面这个图：

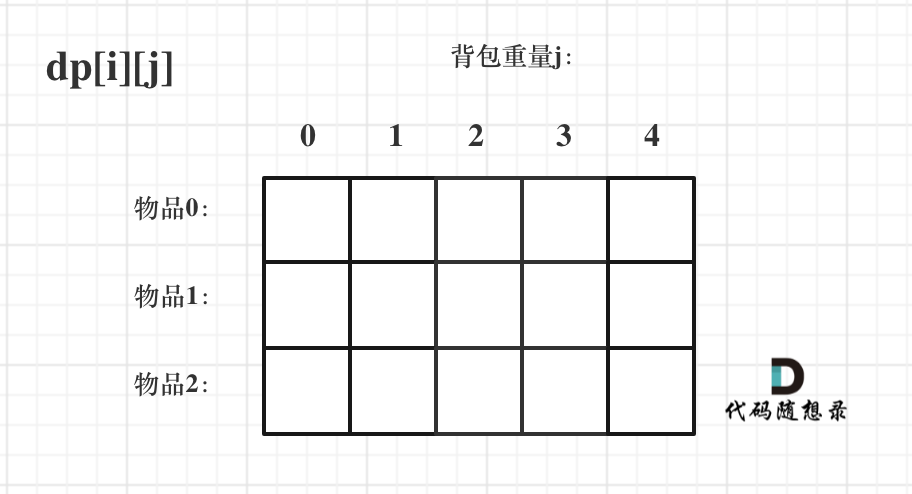
要时刻记着这个dp数组的含义，下面的一些步骤都围绕这dp数组的含义进行的，如果哪里看懵了，就来回顾一下i代表什么，j又代表什么。

2. 确定递推公式

再回顾一下dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

那么可以有两个方向推出来dp[i][j]，

• 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
• 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

3. dp数组如何初始化

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

首先从dp[i][j]的定义出发