ACM算法笔记（七）二分查找与二分答案

二分查找：（又叫折半查找）
算法原理：对查找序列进行有序排列，每一次查找的中间状态，取当前查找区间的中间值，与查找目标比较，从而缩小查找区间，直到查找成功或者查找失败为止。

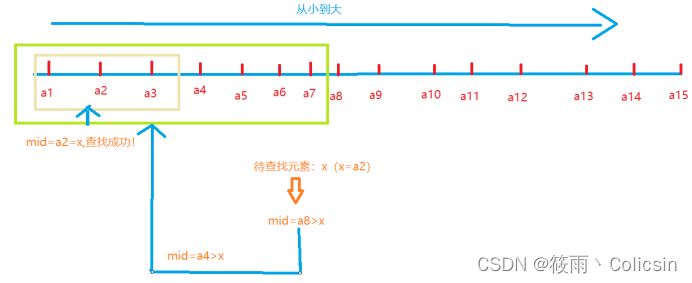
二分查找的时间复杂度分析：
二分查找的查找区间分别是原始长度的1/2、1/4、1/8、1/16，以此类推，对于查询到第i层，搜索区间的长度是原始长度的1/2^i，所以对于长度为n的序列，需要查询log2n次就可以找到答案，时间复杂度为O（nlogn）
二分查找模板代码如下：（朴素版和STL版本）

#include<iostream>
#include<algorithm>
using namespace std;
int a[]={1,7,3,6,16,4,32,5,9,11,10};
int b[]={1,7,3,6,16,4,32,5,9,11,10};
bool flag=false;
void binary_search_(int l,int r,int x)
{
    int mid=(l+r)>>1;
    if(a[mid]==x)
    {
        cout<<"find it!"<<endl;
        flag=true;
    }
    if(x>a[mid]&&l<r)
        binary_search_(mid+1,r,x);
    if(x<a[mid]&&l<r)
        binary_search_(l,mid-1,x);
}
int main()
{
    int n=11;
    sort(a,a+11);
    int x;
    cin>>x;
    binary_search_(0,11,x);
    if(flag==false)
        cout<<"sorry , not find!"<<endl;
    sort(b,b+11);
    /*for(int i=1;i<11;i++)
        cout<<b[i]<<" ";
    cout<<endl;*/
    cout<<"result = "<<binary_search(b,b+11,9)<<endl;//是否找到9这个值
    cout<<"id_ = "<<*lower_bound(b,b+11,9)<<endl;//二分查找第一个>=9的数的值
    cout<<"id- = "<<*upper_bound(b,b+11,9)<<endl;//二分查找第一个>9的数的值
}

二分答案：
前面介绍了二分查找是查找区间折半进行遍历查询所需值，是已知答案，去查询答案是否存在。相对呢二分答案则是确认答案可能存在的区间，然后对区间进行二分，对于每一个二分状态，去验证此状态是否满足条件，若满足，继续向下二分，反之，向上二分，直到得出最优答案。
二分答案的一个常用性质：
在一个有序答案序列[l,r]中，若mid可行，则[l,mid]（或[mid,r]）一定可行，若mid不可行，则[mid,r]（或[l,mid]）一定不可行，操作时那就向着另一个方向进行二分即可。
例一：

解题思路：
由题可知，答案一定在最矮的树的高度到最高的树的高度之间，所以我们对树的高度ai进行升序排序，则答案初始区间可以设定为：[a1,an];然后对于每一个中间二分状态，判断是否满足大于mid的树的高度-mid的和是大于M，满足则说明当前是可以的，继续向下一个区间去遍历。
ps：补充说明一下，对于mid处，若发现∑（ai-x）>=m,则说明，对于当前的mid，是可以满足题目条件即砍掉树木长度之和≥m的，但是此时的mid一定是最优的吗？当然不一定，题目要求的是最长的mid，就是mid的最大值叭，所以mid还可以再大一点，因此向后二分（这里说的是为什么≥m的时候要返回true以向后二分）
代码如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=1e7+7;
long long int a[MAXN],n,m;
bool judge(int x)
{
    long long int M=0;
    for(int i=1;i<=n;i++)
        if(a[i]>x)
            M+=a[i]-x;
    if(M>=m)
        return true;
    else
        return false;
}
int main()
{
    //freopen("1.in","r",stdin);
    //freopen("1.out","w",stdout);
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    sort(a+1,a+1+n);
    long long int l=a[1],r=a[n];
    long long int ans=0;
    while(l<=r)
    {
        long long int mid=(l+r)>>1;
        if(judge(mid)==true)
        {
            ans=mid;
            l=mid+1;
        }
        else
            r=mid-1;
    }
    cout<<ans<<endl;
}

补充：为什么要用二分答案？二分答案的本质是什么思想？
我们依然用这个例一来说明，对于例题一，问给出一个高度使得截取下来的树木长度可以符合要求，并且尽可能地不浪费。比如20 15 10 17这个例子，如果想要得到长度至少为7的木材，那么怎么操作?
假如说把伐木机高度调整为14，如下图

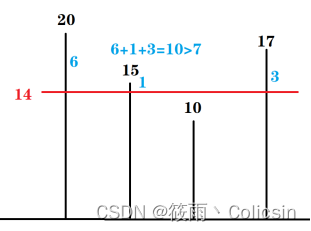
显而易见，这样子得到的树木长度是大于7的，满足条件，但是有价值为3的浪费现象，那么是否满足尽可能不浪费呢？也就是说是不是可以使浪费的价值更小一点呢？
我们试一下伐木机高度为15的情况，如下图

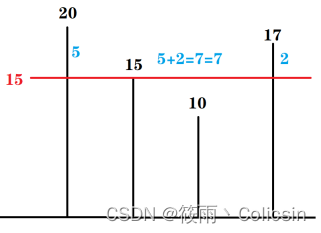
很显然，当伐木机高度为15的时候，依然满足数目长度大于等于7的情况，这个时候发现没有浪费的木材，显然高度为15的时候是最优化的答案。
通过这两个分析，可以得到一个暴力的做法，如果我们抛开时间复杂度去求解，我们可以怎么求？
假设伐木机高度为h，是不是可以使h先等于0，那么获取的树木长度就是20+15+10+17
h如果等于1，那么获取的树木长度就是19+14+9+16
…
h如果等于14，那么获取的树木长度就是6+1+3
h如果等于15，那么获取的树木长度就是5+2
h如果等于16，那么获取的树木长度就是4+1
…
罗列到这可以发现，当h小于等于15，均可以满足获取的树木长度至少为7
当h等于16的时候就不满足了，那么在h=[0，15]区间内开始找，h为多少的时候，满足浪费的最少，那当然是15啦，所以答案就是h=15。
看一看这个思路是什么？不就是枚举暴力破解嘛
写一下暴力代码：

#include<iostream>
using namespace std;
const int MAXN=4e5+7;
int a[MAXN];
int n,m;
bool judge(int x)
{
    int temp=0;
    for(int i=1;i<=n;i++)
        if(a[i]>=x)
            temp+=a[i]-x;
    if(temp>=m)
        return true;
    else
        return false;
}
int main()
{
    cin>>n>>m;
    int maxn=0;
    for(int i=1;i<=n;i++)
        cin>>a[i],maxn=max(maxn,a[i]);
    int res=0;
    for(int i=0;i<=maxn;i++)
    {
        if(judge(i)==true)
            res=max(res,i);
    }
    cout<<res<<endl;
}

这样就是一个最暴力的解法，但是如果数组a的值最大取到1e8的数量级，那么肯定就超时了，所以我们需要对他进行优化，如何优化？二分法！
二分法是一个非常好用的一个优化算法的思想。
我们根据上题可以知道，我们的枚举区间是[0,maxn]，这是一个连续递增的区间，对于每一个循环状态i，这个i都有可能是最终的一个结果，所以我们可以运用二分的思想，不用for循环直接去遍历走一趟O（n），而是二分这个i的结果，直到找到最优的i的值就是答案的解，直接从O（n）优化为O（logn），代码就是上面的那个代码啦。
Ps：再补充说明答案的区间为什么是[0,maxn]，当高度为0的时候肯定是得到的最多的树木，毋庸置疑，当高度为maxn的时候，所获得的树木恰好为0，当高度大于maxn的时候，无疑肯定也是0，这时候再往大去找就没有了任何意义，所以区间右端点是maxn
例二：


思路：每一段的最大值最小为多少，一看便知，老“二分答案”了。针对区间进行二分答案模拟即可，对于每一个中间二分态，模拟其最大值，若前i项ai之和比这个中间态的最大值x还要小，那就继续加，一直加到加和大于x为止，大于x之后说明当前的ai已经不能和前面的划分到一个组里面了，就需要num++，重新开一个划分组，以此算出来当前这个中间态最大值需要有几个划分。但是我们现在还不知道如何判断返回true还是false
分析样例：4 2 4 5 1最多划分成三个划分。
假设最大值是10，那么可以划分为[4,2,4]和[5,1]这样可以划分为两个划分，此时满足num<M
但是我们要求最小的，所以下一步应该模拟中间态最大值为9，判断是否满足。
因此可以得到两个点：在一个二分中间态中，num<=M，返回true。在二分循环中如果满足当前中间态是可以的，那么往小的去搜，所以要执行r=mid-1.
代码如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=1e5+7;
int a[MAXN],N,M;
bool judge(int x)
{
    int num=0;
    int now=0;
    for(int i=1;i<=N;i++)
    {
        if(now+a[i]<=x)
            now+=a[i];
        else
            now=a[i],num++;
    }
    if(num+1<=M)
        return true;
    else
        return false;
}
int main()
{
    cin>>N>>M;
    int ans=0;
    int l=0,r=0;
    for(int i=1;i<=N;i++)
    {
        cin>>a[i];
        l=max(l,a[i]);
        r+=a[i];
    }
    while(l<=r)
    {

        int mid=(l+r)>>1;
        if(judge(mid)==true)
        {
            ans=mid;
            r=mid-1;
        }
        else
            l=mid+1;
    }
    cout<<ans<<endl;
    return 0;
}