【力扣】完全二叉树节点的数量

 🔥博客主页： 我要成为C++领域大神

🎥系列专栏：【C++核心编程】 【计算机网络】 【Linux编程】 【操作系统】

❤️感谢大家点赞👍收藏⭐评论✍️

本博客致力于分享知识，欢迎大家共同学习和交流。

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

 

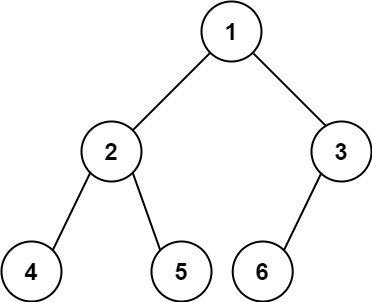
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

---

层序遍历

流程

在队列实现层序遍历的基础上，定义一个count变量，每次遍历完一层时，count加上当前层节点数量

代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr)
            return 0;
        queue<TreeNode*> que;
        que.push(root);
        int count = 0;
        while (!que.empty()) {
            int size = que.size();
            count += size;
            while (size--) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left)
                    que.push(node->left);
                if (node->right)
                    que.push(node->right);
            }
        }
        return count;
    }
};

递归

流程

分别求左子树节点数量，右子树节点数量，然后加上根节点

递归三部曲
确定函数参数和返回值：参数是节点指针，不需要传入其它参数了。返回值是节点数量
确定递归的终止条件：当前节点为空
确定单层递归的逻辑：
求左子树节点个数，右子树节点个数。

代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr)
            return 0;
        return 1 + countNodes(root->left) + countNodes(root->right);
    }
};

利用完全二叉树的特性

流程

我们从一颗树的某一个节点向下分别遍历它的左节点个数和右节点个数，如果左右节点个数相等，那么说明这颗子树是满二叉树

 

 

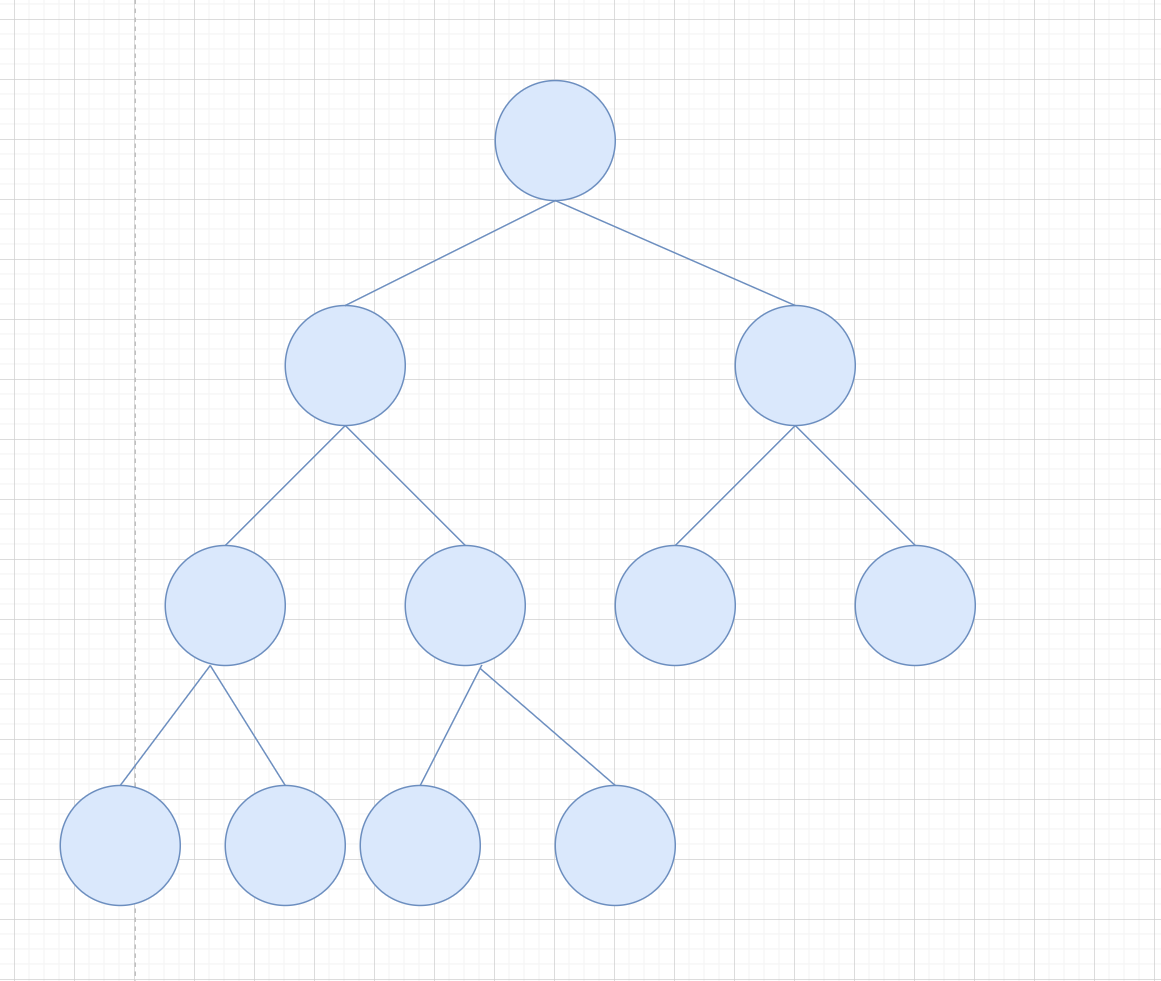
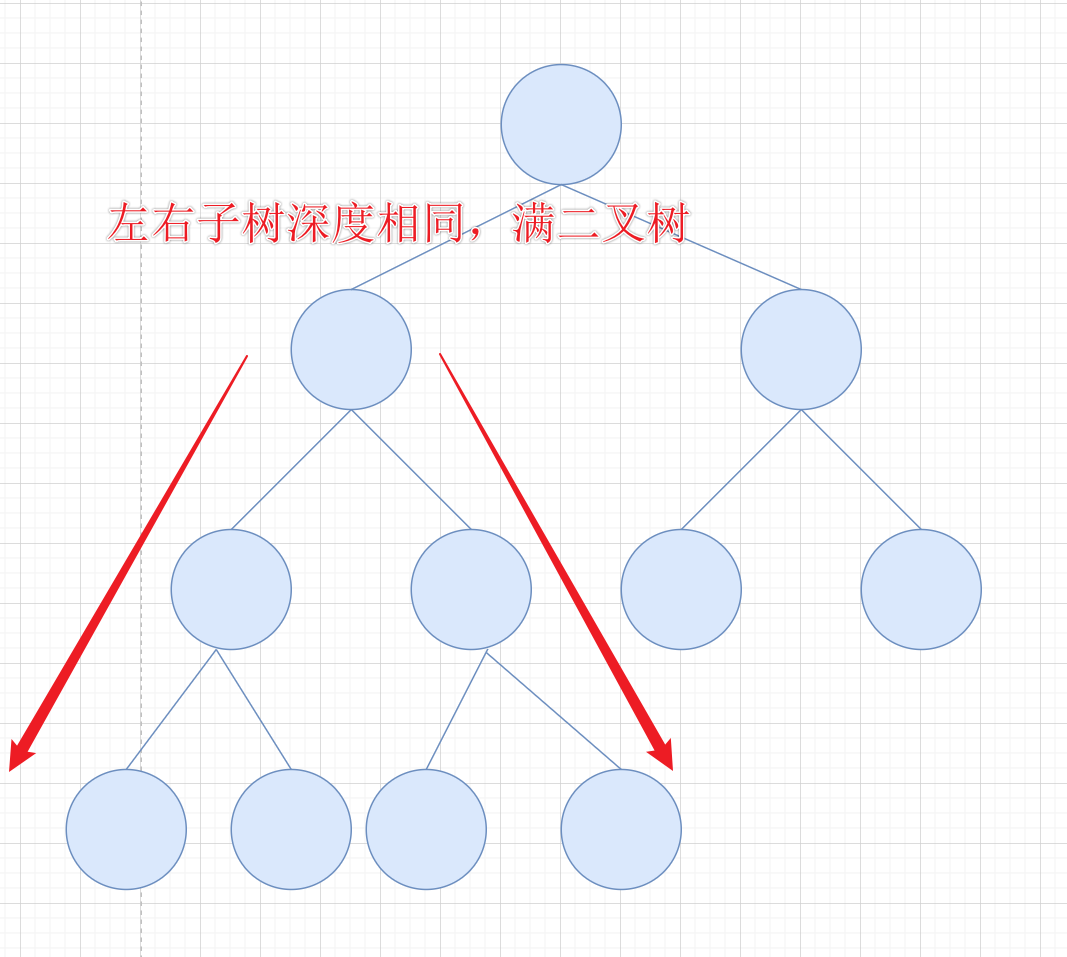
这里容易让人误解的是，没有考虑左子树的右侧，和右子树的左侧是否为空。
因为这是完全二叉树，所以不会出现这种情况

 

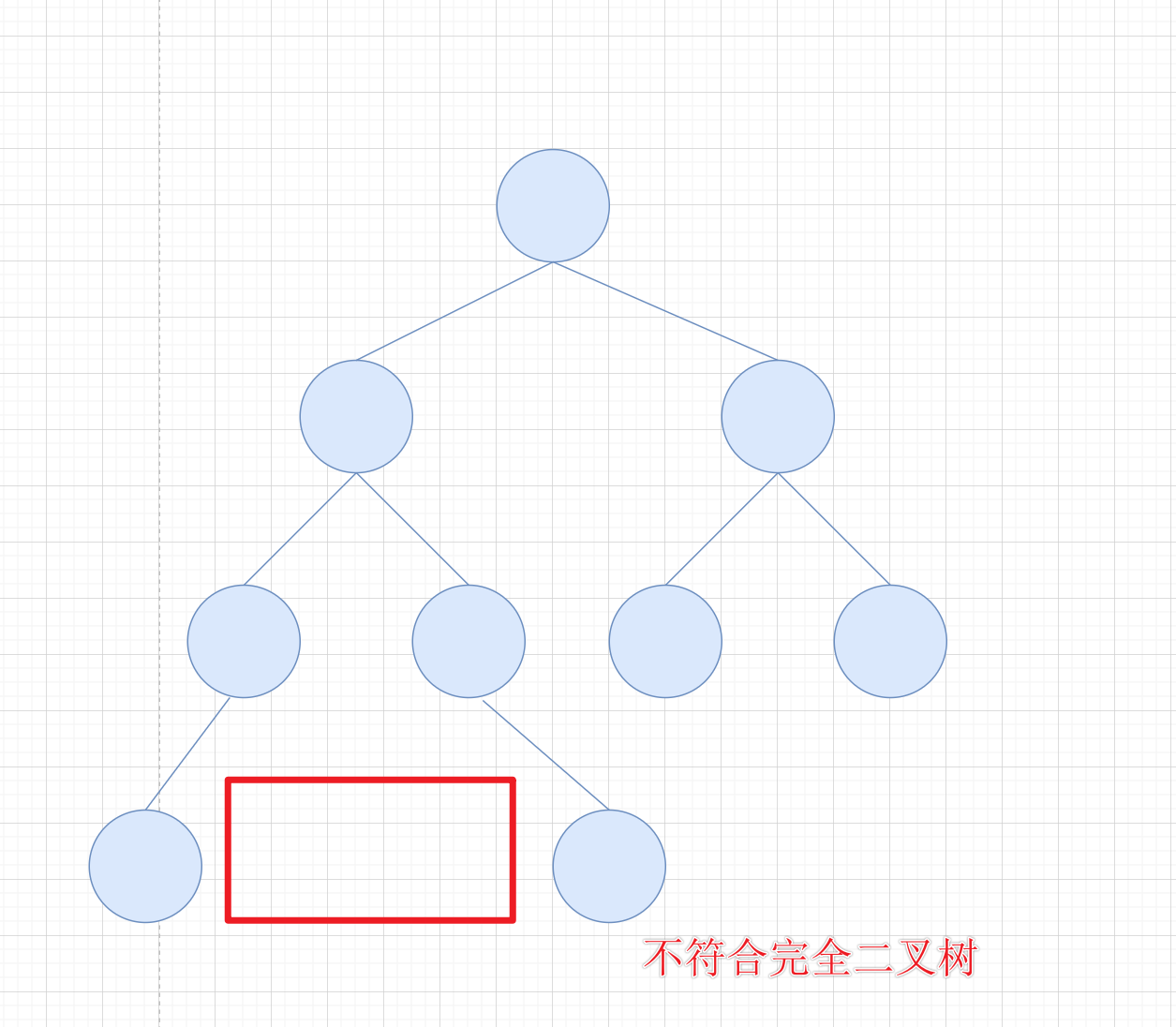
而满二叉树节点个数有计算公式的：2n-1。其中n为满二叉树的深度

代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr)
            return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftDepth = 0;
        int rightDepth = 0;
        while (left) {
            left = left->left;
            leftDepth++;
        }
        while (right) {
            right = right->right;
            rightDepth++;
        }
        if (rightDepth == leftDepth)
            return (2 << leftDepth)-1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

代码比直接用递归要复杂，但是可以节省时间，因为左子树只遍历了左侧，右子树只遍历了右侧。时间复杂度是logn*logn