剑指offer(JS版本)-10-矩形覆盖

题目描述：
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

比如n=3时，2*3的矩形块有3种覆盖方法：

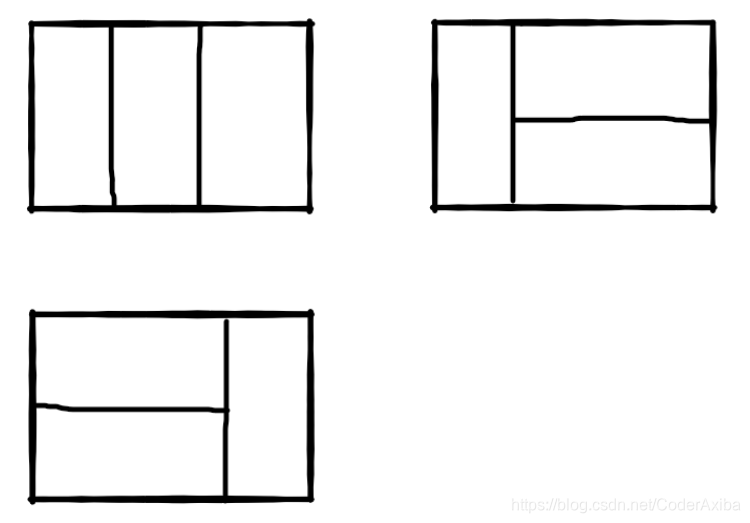
思路：
首先进行推算，
假设大矩形是2×0，那么有0种方法
假设大矩形是2×1，那么只有1种方法
假设是2×2，那么有2种方法
假设有2×3，那么有3种方法
假设有2×4，那么有5种方法
…
观察规律，可发现其方法的序列是0，1，2，3，5，8，13…从3开始之后的序列很明显属于斐波那契序列

代码实现：

function rectCover(number)
{
    // write code here
    if (number === 0){
        return 0;
    } else if (number === 1){
        return 1;
    } else if (number === 2){
        return 2;
    } else {
        var num = [1,2];
        for (var i=3;i<number+1;i++){
            num.push(num[i-2]+num[i-3]);
        }
        return num.pop();
    }
}