比赛速览
本场比赛总体难度较小
- A. 数学小技巧
- B. 概率基础知识
- C. 逆向思维(致谢:高同学)
- D. DFS爆搜(也有人才用轮廓线DP,真没必要)
- E. 括号模型,思维题(代码值得一看)
- F. 线段树优化/两次前缀和优化(本题值得积累)
- G. 网格问题转二分图转费用流
A - Approximation
给AAA和BBB,求距离AB\frac{A}{B}BA最近的整数。
先直接计算出下取整的结果XXX,比较XXX与X+1X+1X+1谁距离AB\frac{A}{B}BA 更近。
但是有更简便的方式,直接使用printf四舍五入。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a, b;
cin >> a >> b;
double t = a * 1.0 / b;
printf("%.0lf\n", t); // 人才
return 0;
}
B - P(X or Y)
骰两个骰子的到AAA和BBB点,计算如下两条规则至少一个满足的概率。
- AAA 与 BBB的和 >=X>= X>=X
- AAA 与BBB的差的绝对值 >=Y>= Y>=Y
本题输出要保留至少101010位小数。
两层循环枚举AAA和BBB,统计至少满足两种条件之一的情况有多少种。除以363636即可。
#include <bits/stdc++.h>
using namespace std;
int main() {
int X, Y, c = 0;
cin >> X >> Y;
for (int i = 1; i <= 6; ++i)
for (int j = 1; j <= 6; ++j)
c += X <= i + j || Y <= abs(i - j);
cout << fixed << setprecision(10);
cout << (double)c / 36 << endl;
}
C - Security 2
致谢:高同学提供C题逆向解题思路
给定一个字符串SSS,请你将初始位空串的TTT变换成SSS。你有两种操作可以任意操作:
- AAA操作可以在TTT的结尾补充一个000
- BBB操作可以让TTT的每一位都+1,9+1+1, 9+1+1,9+1 变成000
求最少的操作次数
1≤∣S∣≤5×1051\leq |S| \leq 5\times 10^51≤∣S∣≤5×105
从数据量上一眼可以看出这应该是个策略贪心。本题实际上只有唯一解,不存在最小解。唯一解就是最小解。题目问最小解实际上是障眼法。
方法一 正向思维
- 考虑BBB操作最特殊,因为BBB操作是一个全局影响的操作,AAA操作只是一个局部影响。
- BBB操作在执行的时候,不会改变数字之间的相对距离。例如原本是
274, 操作B之后变成385, 但是三个数字之间的相对差值不变。所以这是入手点。 - 实际上只要保持TTT的相邻两个数字之间的相对大小 与SSS的对应位置相对大小一致就可以最后通过一些BBB操作使得TTT变成SSS。
- 那么现在只剩下一件事,就是如何保证第222个数字与第111个数字能够保持SSS的模式。
例如:SSS的前两位是27:
- 先做ABBABBABB可以让TTT变成
2 - 然后如果再补充新数字进来只能补充000,无法满足相对值不变。这里需要逆向思维一下。我们知道第二个数字补进来一定是000,所以我们先计算出第一位如果保持相对大小不变应该是:555。 所以应该先把前面的数字搞成555,再补000。 而不是先搞成222。
方法二 逆向思维(来自高同学)
考虑逆向操作,把SSS变成一个空串。那么BBB操作就是整体−1-1−1,然后依次把最后一位数变成000, 然后丢掉。记录下为了把最后一位变成000一共做了多少次BBB,就可以计算出当前位此时是多少了。
#include<bits/stdc++.h>
using namespace std;
int main(){
string s;
cin>>s;
int ans=0;
int res=0;//减了多少
for(int i=s.size()-1;i>=0;i--){
int t=s[i]-'0';
t=(((t-res)%10)+10)%10;
ans+=t+1;
res+=t;
}
cout<<ans;
}
D - Domino Covering XOR
给定一个HHH行WWW列的数阵AAA。你可以在数阵中放置1×21\times 21×2的多米诺骨牌,骨牌不可以交叠,不可以出界。一种放置方案的得分计算规则: 所有未被覆盖的数字的异或和。
- 1≤HW≤201 \leq HW \leq 201≤HW≤20
从复杂度看就是一眼水题,一共202020个位置,枚举每个位置是否被覆盖(先别管骨牌), 然后我们看这个覆盖方案是否合法,即能否找到一个骨牌覆盖出这种模式。剩下的就是暴力计算得分了。
难点在于如何判断覆盖是否合法。那么这个问题本身就有点困难,是一个轮廓线DPDPDP的问题。
换个枚举姿势:每个位置是否放骨牌、放横的骨牌、放竖的骨牌。采用DFSDFSDFS的写法,每次放骨牌就visvisvis标记上覆盖的位置,放的时候也要判断是否会出现交叠和出界。有了这些判断就可以大大缩小复杂度了,实际复杂度不到3203^{20}320。
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, m;
int a[22];
int ans = 0;
bool vis[22];
int id(int x, int y) {
return x * m + y;
}
void dfs(int x) {
if (x >= n*m) {
int res = 0;
for (int i = 0; i < n*m; i++) {
if (!vis[i]) res ^= a[i];
}
ans = max(ans, res);
return;
}
dfs(x+1);
if (vis[x]) return;
int realx = x / m, realy = x % m;
if (realx+1 < n && !vis[x+m]) {
vis[x] = 1;
vis[x+m] = 1;
dfs(x+1);
vis[x] = 0;
vis[x+m] = 0;
}
if (realy+1 < m && !vis[x+1]) {
vis[x] = 1;
vis[x+1] = 1;
dfs(x+1);
vis[x] = 0;
vis[x+1] = 0;
}
}
signed main() {
cin >> n >> m;
for (int i = 0; i < n*m; i++) cin >> a[i];
dfs(0);
cout << ans;
}
E - Most Valuable Parentheses
给定一个长度为2N2N2N的序列AAA,请你构造一个合法的括号序列sss,括号序列的评分规则:所有左括号
(位置iii对应AiA_iAi的总和请你计算最大的得分会是多少。
多组测试样例, 1≤T≤5001\leq T\leq 5001≤T≤500
1≤N≤2×1051 \leq N \leq 2\times 10^51≤N≤2×105
∑N≤2×105\sum N \leq 2\times 10^5∑N≤2×105
从简单的贪心策略上我们肯定希望保留最大的NNN个数字放(, 最小的NNN个数字放)。但是由于前缀合法性的要求,如果前缀中的) 过多了,就必须先放( 进来。
例如:(())) 对于这个情况,前缀出现的333个) 一定有一个要变成(, 那么一定选取最大的一个数字来变。所以我们需要维护前缀中的), 并按照数值从大到小,每次能够取出最大的一个做替换。所以需要优先队列。
综上,我们预先给最大的NNN个数字分配(, 然后从头开始扫描,遇到(不够的时候要选择一个最大的)来变成(, 直到分配完NNN个(就可以了。
这位同学的代码非常简洁, 可以参考一下,思路是一样的,实现很简洁。
#include <bits/stdc++.h>
using namespace std;
priority_queue<int> a;
int main (){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int T;
cin >> T;
for (;T--;){
int n;long long cnt = 0;
cin >> n;
n <<= 1;
for (int i = 1;i <= n;i++){
int x;
cin >> x;
a.push(x);
if (i & 1) cnt += a.top(),a.pop();
}cout << cnt << '\n';a = priority_queue<int>();
}
}
F - Sums of Sliding Window Maximum
给定一个长度为NNN的序列AAA, 对于所有的长度K(1≤K≤N)K (1\leq K \leq N)K(1≤K≤N), 求出所有长度为KKK的子段的MaxMaxMax,并加起来。输出对于每个KKK的结果。
1≤N≤2×1051\leq N \leq 2\times 10^51≤N≤2×105
水题+1+1+1
一眼就是贡献问题,算每个AiA_iAi 会贡献给哪些KKK。
对于全局最大值AiA_iAi来说,只要包含自己的段,自己都是MaxMaxMax,都有贡献:
- 对于长度K=1K=1K=1的子段,AiA_iAi只贡献111次,就是它自己。
- 对于长度K=2K=2K=2的子段,AiA_iAi贡献了222次,就是[Ai−1,Ai][A_{i-1}, A_i][Ai−1,Ai] 和 [Ai,Ai+1][A_i, A_{i+1}][Ai,Ai+1]
- 对于长度K=3K=3K=3的子段,AiA_iAi贡献了333次。
- 以此类推。
但是对于全局第222大的数AjA_jAj来说,就不一样了,他对于每个长度的贡献要考虑最大值AiA_iAi。
如图:
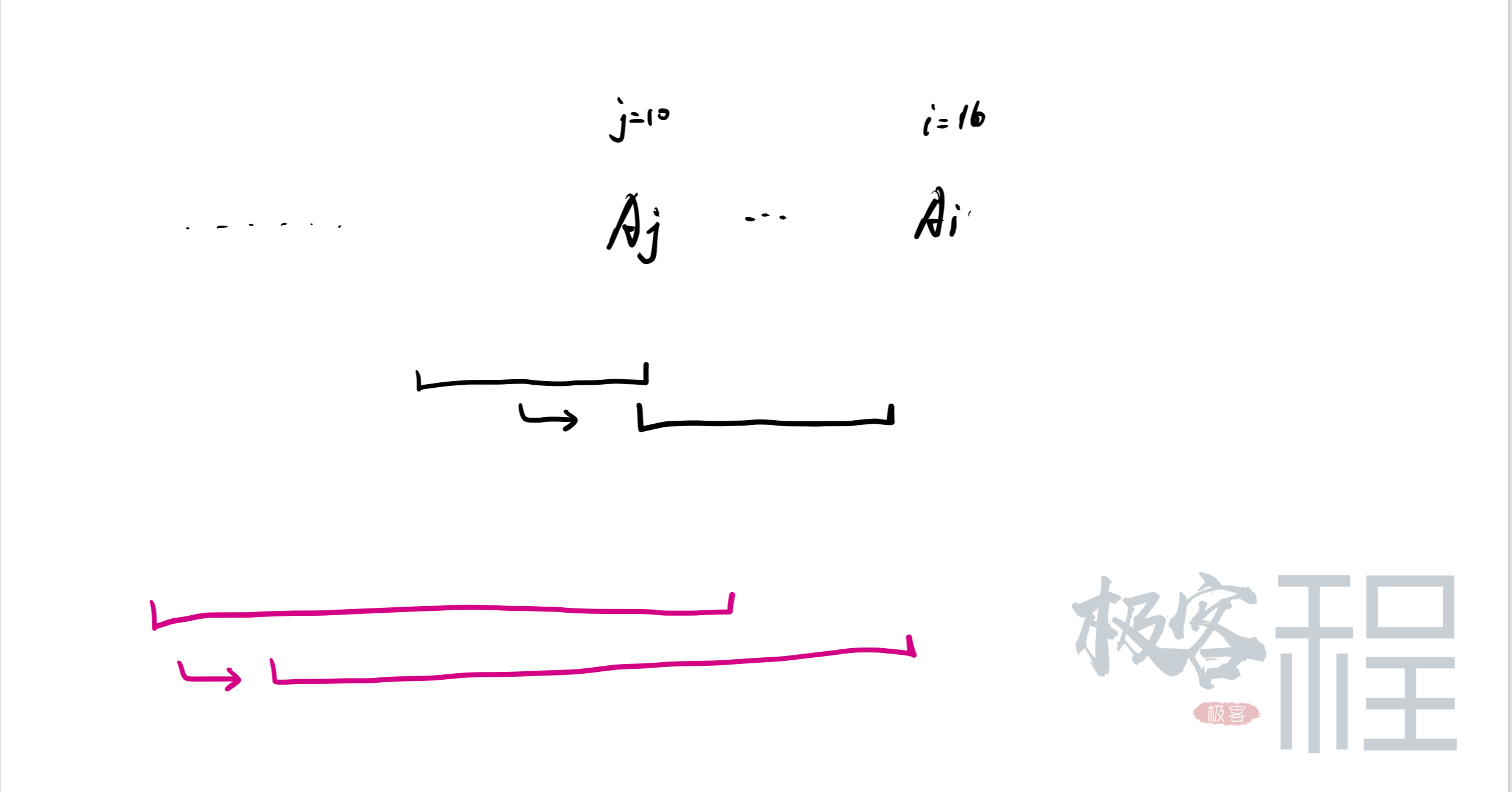
- 对于长度K=1,AjK=1, A_jK=1,Aj贡献111次,
- 对于长度K=2,AjK=2, A_jK=2,Aj贡献222次,
- .........
- 对于长度K=6,AjK=6,A_jK=6,Aj 贡献 贡献了666次。
- 对于长度K=7,AjK=7,A_jK=7,Aj 贡献了666次。
- 对于长度K=8,AjK=8,A_jK=8,Aj 贡献了666次。
- .........
- 对于长度K=10,AjK=10, A_jK=10,Aj 贡献了666次。
- 对于长度K=11,AjK=11, A_jK=11,Aj 贡献了555次。
一般的,对于一个数字AiA_iAi, 其左侧最接近的大于他的数字是ApA_pAp, 右侧最接近的大于他的数字是AqA_qAq, 那么AiA_iAi的贡献规律是:
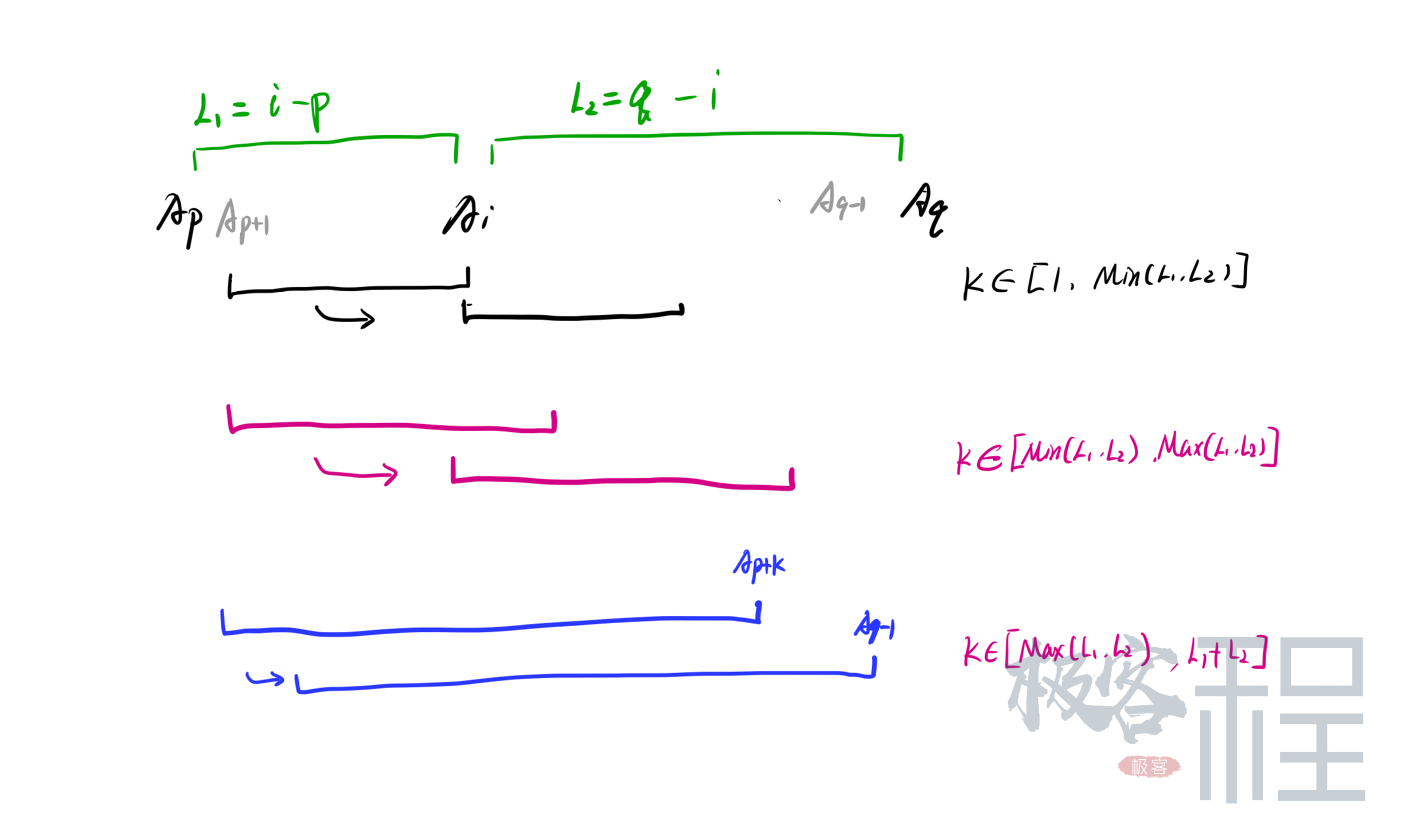
- Case 1. 对于K≤Min(i−p,q−i)K\leq Min(i-p, q-i)K≤Min(i−p,q−i), 贡献KKK次。
- Case 2. 对于Min(i−p,q−i)<K<Max(i−p,q−i)Min(i-p, q-i)< K < Max(i-p,q-i)Min(i−p,q−i)<K<Max(i−p,q−i), 贡献Min(i−p,q−i)Min(i-p, q-i)Min(i−p,q−i)次
- Case 3. 对于Max(i−p,q−i)<K<(q−p)Max(i-p, q-i) < K < (q-p)Max(i−p,q−i)<K<(q−p), 贡献 q−p−Kq-p-Kq−p−K次, 我们可以拆解为贡献q−pq-pq−p次,再去掉KKK次。
代码方法一
这是一个三段式的贡献,并且贡献的值与对象K相关。所以我们需要维护3棵线段树。
- 线段树T1T1T1维护
Case 2的贡献值,和Case 3中q−pq-pq−p部分,区间加值Min(i−p,q−i)×AiMin(i-p,q-i)\times A_iMin(i−p,q−i)×Ai。 - 线段树T2T2T2维护
Case 1中的+K+K+K,对应的操作是区间+Ai+A_i+Ai 和区间−Ai-A_i−Ai, 并对区间结尾后一个位置的单点反向操作。 - 线段树T3T3T3维护
Case 3中的−K-K−K部分, 对应的操作是区间−Ai-A_i−Ai, 并对区间开头的前一个位置的单点反向操作。
最后对于一个K的贡献总和则是(T2的前缀和) + (T3的后缀和) + (T1的单点和)
如果不是很理解T2, 可以考虑这样一个问题:
给定一个序列AAA,每次给区间[L,R][L, R][L,R]中的每个位置iii都加上(i−L+1)∗xi(i-L+1) * x_i(i−L+1)∗xi, 最后求每个位置的值。
注意这里的意思是,给ALA_LAL 加111次xix_ixi, 给AL+1A_{L+1}AL+1加222次xix_ixi, 以此类推。
由于此处区间加值并非是区间统一加同一个值,因此无法直接维护这个值到节点里。
但是我们可以在最后用前缀和的方式来累加这个值,得到最终的结果。即我们给[L,R][L, R][L,R]的每个位置都只加111个xix_ixi, 那么最终的ALA_LAL就是前LLL项和,也就只有111个xi,AL+1x_i,A_{L+1}xi,AL+1 则会把ALA_LAL上加的111个xix_ixi累加到自己身上,最终获得222个xix_ixi, 以此类推。
对于R+1R+1R+1位置我们需要加一个抵消值,用来阻止这一段的xix_ixi累加到后面不需要的位置里。因此我们需要单点对AR+1A_{R+1}AR+1减去一个(R−L+1)∗xi(R-L+1) * x_i(R−L+1)∗xi。
同理考虑T3即可。
代码方法二
对于这种递增次数的贡献方式,我们也可以不用线段树。《算法导论》中就讲过这个知识,如果我们对一个序列做1次前缀和,前面的信息会同步一份给到后面,当我们在第一次基础上再做一次前缀和的时候,前面的信息会递增的传递到后面,即实现了本题的贡献方式。
方法二的代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int MAXN = 2e5 + 25;
int n, a[MAXN];
int L[MAXN], R[MAXN];
ll ans[MAXN];
vector<int>st;
void get_pre() {
for(int i = 1; i <= n; i++) {
ans[i] += ans[i - 1];
}
}
void solve() {
cin >> n;
st.clear();
for(int i = 1; i <= n; i++) {
cin >> a[i];
R[i] = n + 1;
L[i] = 0;
ans[i] = 0;
}
for(int i = 1; i <= n; i++) {
for(; st.size() && a[st.back()] <= a[i]; st.pop_back()) {
R[st.back()] = i;
}
if(st.size())L[i] = st.back();
st.push_back(i);
}
for(int i = 1; i <= n; i++) {
int l = i - L[i], r = R[i] - i;
if(l > r)swap(l, r);
ans[1] += a[i], ans[l + 1] -= a[i], ans[r + 1] -= a[i], ans[l + r + 1] += a[i];
}
// 两次前缀和。
get_pre();
get_pre();
for(int i = 1; i <= n; i++) {
cout << ans[i] << '\n';
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
for(/*cin >> T*/; T--; solve());
return 0;
}
G - Domino Covering SUM
题面背景与D题一致,差异是:
- 数据有正负数,且记分算法变成了求和。
- 矩阵的大小变成了1≤HW≤20001\leq HW \leq 20001≤HW≤2000
本题需要转为图结构来解决。
如果我们将格点看作是点,将相邻看作是连边。则这个图以相邻关系绘制出图会是一个二部图。(自行证明,可以黑白染色,也可以反证法)
定义边权为两点上数字之和。则原问题最大化剩余点的权值之和,等价于最小化边集。但是我们不知道要选多少条边,但是我们可以枚举选多少条边。
考虑另外一个问题:
对于一个正边权二分图来说,寻找最小的K匹配问题。即只选择K个匹配,保证K个匹配的边权之和最小。
这个问题我们可以使用最小费用最大流来解决。
本题只要先把所有边权都加101210^{12}1012,就变成了上面全正权边的问题,最后再统一减掉就可以了。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








