程序员面试必备——动画详解十大经典排序算法（C语言版）

博客原文地址

排序算法是程序员必备的基础知识，弄明白它们的原理和实现很有必要。本文中将通过非常细节的动画展示出算法的原理，配合代码更容易理解。

概述

由于待排序的元素数量不同，使得排序过程中涉及的存储器不同，可将排序方法分为两类：一类是内部排序，指的是待排序列存放在计算机随机存储器中进行的排序过程；另一类是外部排序，指的是待排序的元素的数量很大，以致内存一次不能容纳全部记录，在排序过程中尚需对外存进行访问的排序过程。

我们可以将常见的内部排序算法可以分成两类：

比较类排序：通过比较来决定元素间的相对次序，时间复杂度为 O(nlogn)～O(n²)。属于比较类的有：

排序算法	时间复杂度	最差情况	最好情况	空间复杂度	排序方式	稳定性
冒泡排序	O(n²)	O(n²)	O(n)	O(1)​	In-place	✔
快速排序	O(nlogn)​	O(n²)	O(nlogn)​	O(logn)​	In-place	✘
插入排序	O(n²)	O(n²)	O(n)​	O(1)​	In-place	✔
希尔排序	O(nlog²n)​	O(n²)	O(n)​	O(1)​	In-place	✘
选择排序	O(n²)	O(n²)	O(n²)	O(1)​	In-place	✘
堆排序	O(nlogn)​	O(nlogn)	O(nlogn)​	O(1)​	In-place	✘
归并排序	O(nlogn)​	O(nlogn)	O(nlogn)​	O(n)​	Out-place	✔

非比较类排序：不通过比较来决定元素间的相对次序，其时间复杂度可以突破 O(nlogn)，以线性时间运行。属于非比较类的有：

排序算法	时间复杂度	最差情况	最好情况	空间复杂度	排序方式	稳定性
桶排序	O(n+nlog(n/r))​	O(n²)	O(n)​	O(n+r)​	Out-place	✔
计数排序	O(n+r)​	O(n+r)​	O(n+r)​	O(n+r)​	Out-place	✔
基数排序	O(d(n+r))​	O(d(n+r))	O(d(n+r))	O(n+r)​	Out-place	✔

名词解释：

时间/空间复杂度：描述一个算法执行时间/占用空间与数据规模的增长关系

n：待排序列的个数

r：“桶”的个数（上面的三种非比较类排序都是基于“桶”的思想实现的）

d：待排序列的最高位数

In-place：原地算法，指的是占用常用内存，不占用额外内存。空间复杂度为 O(1) 的都可以认为是原地算法

Out-place：非原地算法，占用额外内存

稳定性：假设待排序列中两元素相等，排序前后这两个相等元素的相对位置不变，则认为是稳定的。

冒泡排序

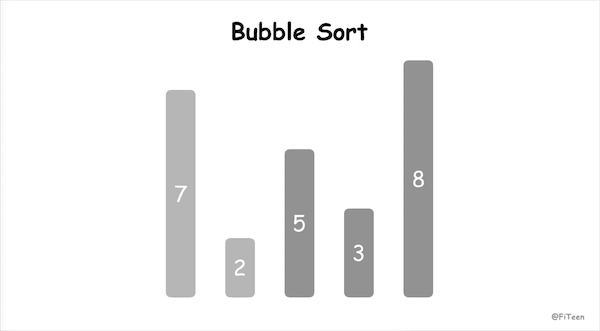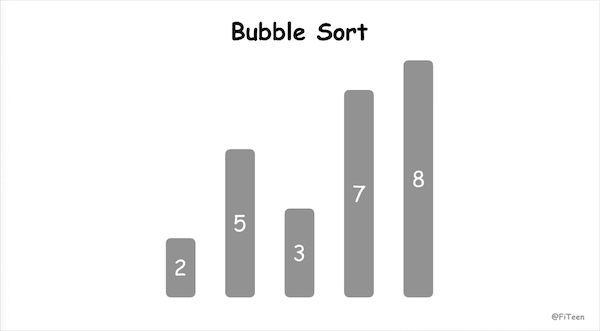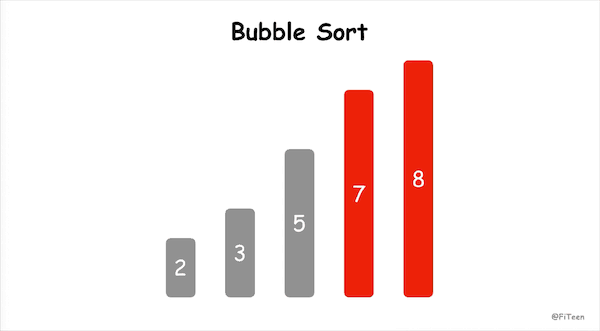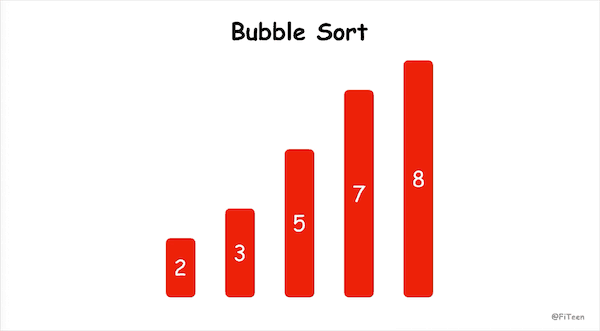
冒泡排序（Bubble Sort），顾名思义，就是指越小的元素会经由交换慢慢“浮”到数列的顶端。

算法原理

1. 从左到右，依次比较相邻的元素大小，更大的元素交换到右边；
2. 从第一组相邻元素比较到最后一组相邻元素，这一步结束最后一个元素必然是参与比较的元素中最大的元素；
3. 按照大的居右原则，重新从左到后比较，前一轮中得到的最后一个元素不参与比较，得出新一轮的最大元素；
4. 按照上述规则，每一轮结束会减少一个元素参与比较，直到没有任何一组元素需要比较。

动图演示

代码实现

void bubble_sort(int arr[], int n) {
   
    int i, j;
    for (i = 0; i < n - 1; i++) {
   
        for (j = 0; j < n - i - 1; j++) {
   
            if (arr[j] > arr[j + 1]) {
   
                swap(arr, j, j+1);
            }
        }
    }
}

算法分析

冒泡排序属于交换排序，是稳定排序，平均时间复杂度为 O(n²)，空间复杂度为 O(1)。

但是我们常看到冒泡排序的最优时间复杂度是 O(n)，那要如何优化呢？

我们可以用一个 flag 参数记录新一轮的排序中元素是否做过交换，如果没有，说明前面参与比较过的元素已经是正序，那就没必要再从头比较了。代码实现如下：

void bubble_sort_quicker(int arr[], int n) {
   
    int i, j, flag;
    for (i = 0; i < n - 1; i++) {
   
        flag = 0;
        for (j = 0; j < n - i - 1; j++) {
   
            if (arr[j] > arr[j + 1]) {
   
                swap(arr, j, j+1);
                flag = 1;
            }
        }
        if (!flag) return;
    }
}

快速排序

快速排序（Quick Sort），是冒泡排序的改进版，之所以“快速”，是因为使用了分治法。它也属于交换排序，通过元素之间的位置交换来达到排序的目的。

基本思想

在序列中随机挑选一个元素作基准，将小于基准的元素放在基准之前，大于基准的元素放在基准之后，再分别对小数区与大数区进行排序。

一趟快速排序的具体做法是：

1. 设两个指针 i 和 j，分别指向序列的头部和尾部；
2. 先从 j 所指的位置向前搜索，找到第一个比基准小的值，把它与基准交换位置；
3. 再从 i 所指的位置向后搜索，找到第一个比基准大的值，把它与基准交换位置；
4. 重复 2、3 两步，直到 i = j。

仔细研究一下上述算法我们会发现，在排序过程中，对基准的移动其实是多余的，因为只有一趟排序结束时，也就是 i = j 的位置才是基准的最终位置。

由此可以优化一下算法：

1. 设两个指针 i 和 j，分别指向序列的头部和尾部；
2. 先从 j 所指的位置向前搜索，找到第一个比基准小的数值后停下来，再从 i 所指的位置向后搜索，找到第一个比基准大的数值后停下来，把 i 和 j 指向的两个值交换位置；
3. 重复步骤2，直到 i = j，最后将相遇点指向的值与基准交换位置。

动图演示

代码实现

这里取序列的第一个元素为基准。

/* 选取序列的第一个元素作为基准 */
int select_pivot(int arr[], int low) {
   
    return arr[low];
}

void quick_sort(int arr[], int low, int high) {
   
    int i, j, pivot;
    if (low >= high) return;
    pivot = select_pivot(arr, low);
    i = low;
    j = high;
    while (i != j) {
   
        while (arr[j] >= pivot && i < j) j--;
        while (arr[i] <= pivot && i < j) i++;
        if (i < j) swap(arr, i, j);
    }
    arr[low] = arr[i];
    arr[i] = pivot;
    quick_sort(arr, low, i - 1);
    quick_sort(arr, i + 1, high);
}

算法分析

快速排序是不稳定排序，它的平均时间复杂度为 O(nlogn)，平均空间复杂度为 O(lo