【贪心】会场安排问题

贪心算法总是做出当前看来是最好的选择（局部最优—>整体最优）

一.基本要素

1.贪心选择性质：局部最优—>整体最优

2.最优子结构性质：一个问题的最优解包含其子问题的最优解。

二.贪心算法和动态规划算法的差异

动态规划算法：每步所做出的选择往往依赖于相关子问题的解，因而只有在解出相关子问题后才能做出选择。

贪心算法：仅在当前状态下做出最好选择，即局部最优选择，再去解做出这个选择后产生的相应子问题。贪心算法所做的贪心选择可以依赖以往所做过的选择，但绝不依赖将来所做的选择，也不依赖子问题的解。

三.局限性

1.贪心算法不是对所有问题都能得到整体最优解

2.不能用来求最大最小解问题

四.例题-会场安排问题

1.问题描述

2.算法思路

1.将所有活动安排按照开始时间从小到大排序

2.安排第一个活动肯定需要一个会场，故初始cnt=1，记录结束时间

3.开一个数组hall[]记录所有会场最近活动的结束时间

4.遍历所有活动，如果当前活动的开始时间大于某个会场最近活动的结束时间，则该会场可举办该活动，更新该会场最近活动的结束时间；如果当前活动的开始时间小与所有会场最近活动的结束时间，则需新租一个会场

3.程序代码

#include<bits/stdc++.h>
using namespace std;
#define N 100100
struct act{
	int s;
	int e;
}a[N];
int k;
int hall[N];

bool com(act left,act right){
	return left.s<right.s;
}

int main(){
	scanf("%d",&k);
	for(int i=1;i<=k;i++){
		scanf("%d",&a[i].s);
		scanf("%d",&a[i].e);
	}
	sort(a+1,a+k,com);
	int cnt=1;
	hall[1]=a[1].e;
	for(int i=2;i<=k;i++){
		for(int j=1;j<=cnt+1;j++){
			//现有场馆不能用 
			if(j==cnt+1){
				cnt++;
				hall[cnt]=a[i].e; //新弄一个场馆
				break; 
			}
			//现有场馆可以用 
			if(a[i].s>hall[j]){
				hall[j]=a[i].e;
				break;
			}
		}
	}
	printf("%d",cnt);
	return 0;
} 

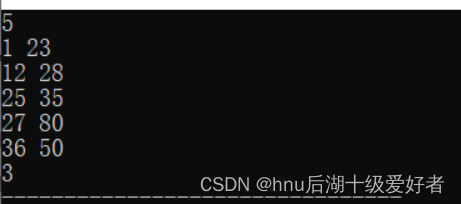
4.测试