C++实现七大排序算法

七大排序方法比较：

排序方法	平均情况	最好情况	最坏情况	辅助空间	稳定性
冒泡排序	O(N2)	O(N)	O(N2)	O(1)	稳定
选择排序	O(N2)	O(N2)	O(N2)	O(1)	不稳定
插入排序	O(N2)	O(N)	O(N2)	O(1)	稳定
希尔排序	O(NlogN)-O(N2)	O(N1.3)	O(N2)	O(1)	不稳定
堆排序	O(NlogN)	O(NlogN)	O(NlogN)	O(1)	不稳定
归并排序	O(NlogN)	O(NlogN)	O(NlogN)	O(N)	稳定
快速排序	O(NlogN)	O(NlogN)	O(N2)	O(logN)-O(N)	不稳定

1. 冒泡排序

        如下图所示，在第一轮排序中，以此对比相邻的两个数的大小，将较大的值交换之后面的位置，最后实现将待排序数组中的最大值移动到了最后一个位置。

        在第二轮的排序中，对前9个待排序数组的元素进行上述排序过程，直至完成所有的排序。

        可以发现，如果在一轮排序过程中没有发现元素的交换，那么该数组已经有序，借助该发现，可以提前结束循环。

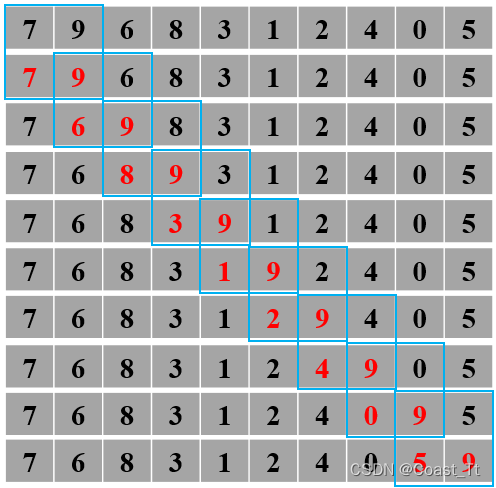
//O(n^2) 冒泡排序(交换排序)->稳定排序
void bubbleSort(vector<int> &a)
{
    int n = a.size();
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = 0; j < n - 1 - i; j++)
        {
            if(a[j] > a[j+1])
            {
                int temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
        }
    }
}

// 优化1：外循环加flag 若有一趟排序中无交换，则提前结束循环
void bubbleSort2(vector<int> &a)
{
    int flag = 1;
    int n = a.size();
    for (int i = 0; i < n - 1 && flag; i++)
    {
        flag = 0;
        for (int j = 0; j < n - 1 - i; j++)
        {
            if(a[j] > a[j+1])
            {
                flag = 1;
                int temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
        }
    }
}

// 优化2：外循环加flag，内循环记录最后一次交换的位置
void bubbleSort2(vector<int> &a)
{
    int flag = 1;
    int lastExchangeIndex = 0;
    int sortBorder = n - 1;
    int n = a.size();
    for (int i = 0; i < n - 1 && flag; i++)
    {
        flag = 0;
        for (int j = 0; j < sortBorder; j++)
        {
            if(a[j] > a[j+1])
            {
                flag = 1;
                int temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
                lastExchangeIndex = j;
            }
        }
        sortBorder = lastExchangeIndex;
    }
}

2. 选择排序

        如下图所示，旋转排序在每一轮排序时，选择待排序数组内最小的元素，记录下其位置，与第i个元素进行排序。i代表第几轮排序的轮数。

 

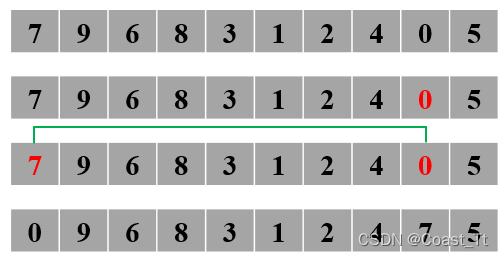
//O(n^2) 选择排序(选择排序)->稳定排序
void selectSort(vector<int> &a)
{
    int n = a.size();
    for (int i = 0; i < n; i++)
    {
        int min = a[i];
        int min_index = i;
        for (int j = i + 1; j < n; j++)
        {
            if(a[j] < min)
            {
                min = a[j];
                min_index = j;
            }
        }
        int temp = a[min_index];
        a[min_index] = a[i];
        a[i] = temp;
    }
}

3. 插入排序

//O(n^2) 直接插入排序(插入排序)->稳定排序
void insertSort(vector<int> &a)
{
    int n = a.size();
    for (int i = 1; i < n; i++)
    {
        for (int j = i - 1; j >= 0 && a[j+1] < a[j]; j--)
        {
            int temp = a[j];
            a[j] = a[j + 1];
            a[j + 1] = temp;
        }
    }
}

void insertSort2(vector<int> &a)
{
    int n = a.size();
    int i, j, temp;
    for (i = 1; i < n; i++)
    {
        temp = a[i];
        for (j = i - 1; j >= 0 && temp < a[j]; j--)
        {
            a[j + 1] = a[j];
        }
        a[j + 1] = temp;
    }
}

void insertSort3(vector<int> &a)
{
    int n = a.size();
    int i, j, temp;
    //把希尔排序的d换成1
    for (i = 1; i < n; i++)
    {
        temp = a[i];
        for (j = i; j >= 1 && temp < a[j - 1]; j--)
        {
            a[j] = a[j - 1];
        }
        a[j] = temp;
    }
}

4. 希尔排序

//O(nlogn) - (n^2) 希尔排序(插入排序)->不稳定排序
void shellSort(vector<int> &a)
{
    int i, j, d, temp;
    int n = a.size();
    for(d = n / 2; d > 0; d /= 2)
    {
        //相当于多次插入排序 把插入排序的1换成d
        for (i = d; i < n; i++)
        {
            temp = a[i];
            for (j = i; j >= d && temp < a[j - d]; j -= d)
                a[j] = a[j - d];
            a[j] = temp;
        }
    }
}

5. 堆排序

#include <iostream>
#include <vector>
using namespace std;

void swap(vector<int> &tree, int i, int j)
{
    int temp = tree[i];
    tree[i] = tree[j];
    tree[j] = temp;
}

//对一个节点做heapify的时候，必须保证它的所有子树都已经是堆
void heapify(vector<int> &tree, int n, int root)
{
    //自上而下
    if(root >= n)
        return;

    int max = root;
    int lchild = 2 * root + 1;
    int rchild = 2 * root + 2;

    if(lchild < n && tree[lchild] > tree[max])
        max = lchild;
    if(rchild < n && tree[rchild] > tree[max])
        max = rchild;

    if(max != root)
    {
        swap(tree, root, max);
        heapify(tree, n, max); //与哪边交换就破坏了哪边子树的堆结构
    }
}

//构造大顶堆
void build_heap(vector<int>&tree, int n)
{
    //自下而上
    int last_node = n - 1;
    int parent = (last_node - 1) / 2;
    for (int i = parent; i >= 0; i--)
    {
        heapify(tree, n, i);
    }
}

void heap_sort(vector<int> &tree, int n)
{
    build_heap(tree, n);

    for (int i = n - 1; i >= 0;i--)
    {
        swap(tree, i, 0);    //将大顶堆的顶点作为最大值交换到后面
        heapify(tree, i, 0); //交换后只破坏最上方的堆结构
    }
}

int main()
{
    vector<int> tree = {2, 5, 3, 1, 10, 4};
    heap_sort(tree, tree.size());

    for (int val:tree)
        cout << val << " ";
    cout << endl;
    system("pause");
    return 0;
}

6. 归并排序

#include <iostream>
#include <vector>
using namespace std;

//O(nlogn) 归并排序(插入排序)->稳定排序
void merge(vector<int>& v, int L, int M, int R)
{
    int leftSize = M - L;
    int rightSize = R - M + 1;
    int i, j, k;
    vector<int> left(leftSize);
    vector<int> right(rightSize);

    //拆分为左右两部分
    for (i = L; i < M; i++)
    {
        left[i - L] = v[i];
    }

    for (i = M; i <= R; i++)
    {
        right[i - M] = v[i];
    }

    //将左右有序合并到原始数组
    i = 0;
    j = 0;
    k = L;
    while(i < leftSize && j < rightSize)
    {
        if(left[i] < right[j])
        {
            v[k++] = left[i++];
        }
        else
        {
            v[k++] = right[j++];
        }
    }

    while(i < leftSize)
    {
        v[k++] = left[i++];
    }

    while(j < rightSize)
    {
        v[k++] = right[j++];
    }
}

void mergeSort(vector<int>& v, int L, int R)
{
    if(L == R)
        return;
    else
    {        
        int M = (L + R) / 2;
        mergeSort(v, L, M);
        mergeSort(v, M + 1, R);
        merge(v, L, M + 1, R);
    }
}
int main()
{
    vector<int> v1 = {9, 7, 6, 8, 3, 1, 2, 4, 0, 5};
    mergeSort(v1, 0, v1.size() - 1);
    for(int val:v1)
        cout << val << " ";
    cout << endl;
    system("pause");
    return 0;
}

8. 快速排序

#include <iostream>
#include <vector>
using namespace std;

//O(nlogn) 快速排序(排序)->不稳定排序
void quickSort(vector<int>& a, int left, int right)
{
    if(left >= right)
        return;
    int i, j, base, temp;
    i = left;
    j = right;
    base = a[left]; //基准数
    while(i < j)
    {
        while(a[j] >= base && i < j)
            j--; //从右边找到小于base的数
        while(a[i] <= base && i < j)
            i++; //从左边找到大于base的数
        if(i < j)
        {
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }
    }
    //i与j相遇，则与基准数交换
    a[left] = a[i];
    a[i] = base;

    quickSort(a, left, i - 1);  //递归左边
    quickSort(a, i + 1, right); //递归右边
}
int main()
{
    vector<int> v1 = {9, 7, 6, 8, 3, 1, 2, 4, 0, 5};
    quickSort(v1, 0, v1.size() - 1);
    for(int val:v1)
        cout << val << " ";
    cout << endl;
    system("pause");
    return 0;
}