基于KNN的手写数字识别

原创于 2024-12-16 22:22:48 发布 · 1.7k 阅读

41 ·

CC 4.0 BY-SA版权

文章标签：

#python

部署运行你感兴趣的模型镜像

实验描述

数据集

semeion_test.csv, semeion_test.csv

实验基本要求

编程实现kNN算法；给出在不同k值(1，3，5)情况下，kNN算法对手写数字的识别精度

实验中级要求

与Python机器学习包中的kNN分类结果进行对比

具体分析

导入库 import numpy as np

读取实验数据将训练集和数据集中的数据读取, 转化为二维数组

def read_space_separated_csv(filename):  
  
    float_rows = []  
    int_rows = []  
  
    # 读取文件内容  
  
  with open(filename, 'r') as file:  
        lines = [line.strip() for line in file.readlines()]  
  
    # 遍历每一行数据  
  for line in lines:  
  
    # 使用空格分割数据  
  columns = line.split()  
  
    # 将前total_columns-10列转换为浮点数，并添加到浮点数行列表中  
  float_cols = [float(col) for col in columns[: - 10]]  
        float_rows.append(float_cols)  
  
    # 将后10列转换为整数，并添加到整数行列表中  
  int_cols = [int(col) for col in columns[ - 10:]]  
        int_rows.append(int_cols)  
  
    # 将列表转换为NumPy二维数组  
  float_array = np.array(float_rows)  
    int_array = np.array(int_rows)  
  
    # 返回两个NumPy二维数组  
  return float_array, int_array  
  
train_X,train_y = read_space_separated_csv("semeion_train.csv")  
test_X,test_y = read_space_separated_csv("semeion_test.csv")  
train_y = np.argmax(train_y, axis=1)  
test_y = np.argmax(test_y, axis=1)

KNN算法实现将k值、训练集、训练集结果、测试集作为函数的输入。计算待识别元素与训练集中各个元素的欧氏距离，并选出欧式距离最小的k个训练集数据。根据这k个结果，对输入数据分类。

   class KNN:  
    def __init__(self,k):  
        self.k = k  
    def fit(self,train_X,train_y):  
        self.train_X = np.asarray(train_X)  
        self.train_y = np.asarray(train_y)  
    def predict(self,test_X):  
        X = np.asarray(test_X)  
        result = []  
        for x in X:  
            dis = np.sqrt(np.sum((x - self.train_X) ** 2, axis=1))  # 对于测试机的每隔一个样本，一次与训练集的所有数据求欧氏距离``````  

  index = dis.argsort()  # 返回排序结果的下标  
  index = index[:self.k]  # 截取前K个  
  count = np.bincount(self.train_y[index])  # 返回数组中每个整数元素出现次数，元素必须是非负整数  
  result.append(count.argmax())  # 返回ndarray中值最大的元素所对应的索引，就是出现次数最多的索引，也就是我们判定的类别  
  return np.asarray(result)

测试集结果准确率计算

def simrate(y_predict,test_y):  
    percent = 0  
  percent =np.sum(y_predict == test_y)/len(test_y)  
    return format(percent, '.2%')  
  
knn1 = KNN(1)  
knn3 = KNN(3)  
knn5 = KNN(5)  
knn1.fit(train_X,train_y)  
result1 = knn1.predict(test_X)  
knn3.fit(train_X,train_y)  
result3 = knn3.predict(test_X)  
knn5.fit(train_X,train_y)  
result5 = knn5.predict(test_X)  
  
  
  
print("knn中k = 1时的准确率是：",simrate(result1,test_y))  
print("knn中k = 3时的准确率是：",simrate(result3,test_y))  
print("knn中k = 5时的准确率是：",simrate(result5,test_y))  
  
from sklearn.neighbors import KNeighborsClassifier  
knn1 = KNeighborsClassifier(1)  
knn1.fit(train_X, train_y)  
knn3 = KNeighborsClassifier(3)  
knn3.fit(train_X, train_y)  
knn5 = KNeighborsClassifier(5)  
knn5.fit(train_X, train_y)  
resultsk1 = knn1.predict(test_X)  
resultsk3 = knn3.predict(test_X)  
resultsk5 = knn5.predict(test_X)  
print("sklearn中k = 1时的准确率是：", simrate(resultsk1,test_y))  
print("sklearn中k = 3时的准确率是：", simrate(resultsk3,test_y))  
print("sklearn中k = 5时的准确率是：", simrate(resultsk5,test_y))

实验结果

实验结果截图如下

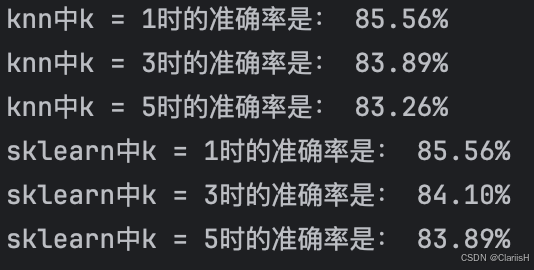
可以看出，knn中k = 1时的准确率是： 85.56%，sklearn中k = 1时的准确率是： 85.56%，准确率持平 knn中k = 3时的准确率是： 83.89%，sklearn中k = 3时的准确率是： 84.10%，准确率略低 knn中k = 5时的准确率是： 83.26%，sklearn中k = 5时的准确率是： 83.89%，准确率略低

由此可以得出结论：