DatawhaleAI夏令营笔记 X 李宏毅苹果树
Task1
1. 机器学习基础
1.1内涵
机器具备学习的能力,即让机器具备找一个函数的能力
1.2类别
1.2.1回归
通过函数输出一个数值
如预测未来某个时间的PM2.5
1.2.2分类
让机器做选择
如判断邮件是否为垃圾邮件
1.2.3结构化学习
产生一个有机构的物体
如让机器画一张画
1.3找函数的步骤
1.3.1 写出一个带有未知参数的函数
如 y = wx + b
x: Feature
w: weight
b: bias
1.3.2定义损失
1.3.2.1损失函数
L = L(b,w)
1.3.2.2平均绝对误差(MAE)
e=∣yˆ−y∣ e = |yˆ − y| e=∣yˆ−y∣
1.3.2.3均方误差(MSE)
e=(yˆ−y)2 e = (yˆ − y)2 e=(yˆ−y)2
1.3.3最优化
1.3.3.1梯度下降
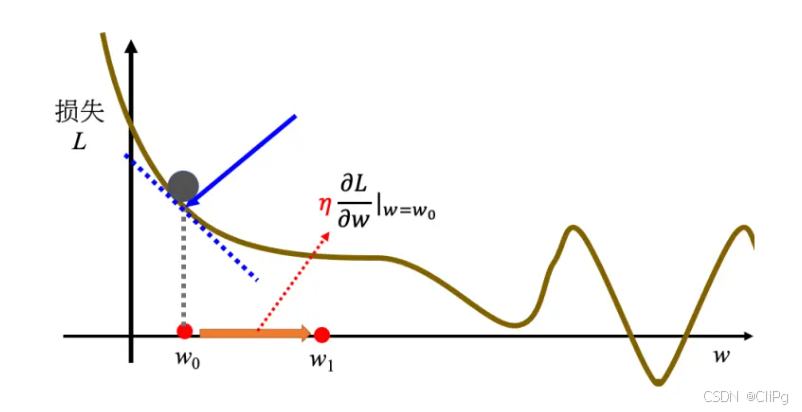
假设这里有一个损失函数
L = L(w)
随机假设一个点w0,可以计算函数在该点处的微分
w1←w0−η∂L∂w∣w=w0
w_{1} \leftarrow w_{0} - \eta \frac{\partial L}{\partial w} |_{w=w_{0}}
w1←w0−η∂w∂L∣w=w0
`
从中可以发现斜率绝对值越大,移动的步伐越大,斜率为正向左移,为负向右移,不断迭代可以找到一个极值点,称为局部最小值,但不一定是全局最小值,这与w0有关
η:学习率
影响步伐大小,由自己设定,称为超参数
Task2
2.线性模型
2.1概念
把输入的特征 x 乘上一个权重,再加上一个偏置得到预测的结果
2.2HardSigmoid
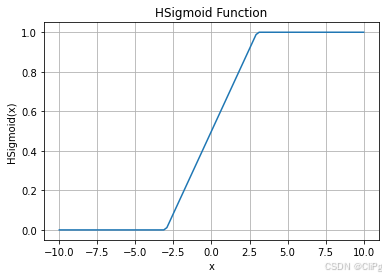
特性:Hard Sigmoid 函数的特性是当输入的值,当 x 轴的值小于某一个阈值(某个定值)的时候,大于另外一个定值阈值的时候,中间有一个斜坡。所以它是先水平的,再斜坡,再水平的。
2.3分段线性曲线
但是如果只是单纯的线性模型,函数终归只是一条斜线,无法变得曲折,因此我们引入分段线性曲线
通过分段线性曲线,我们可以将折线图像化作若干HardSigmod函数的和
同理对于曲线图像,我们可以在曲线上取若干个点,化曲为直
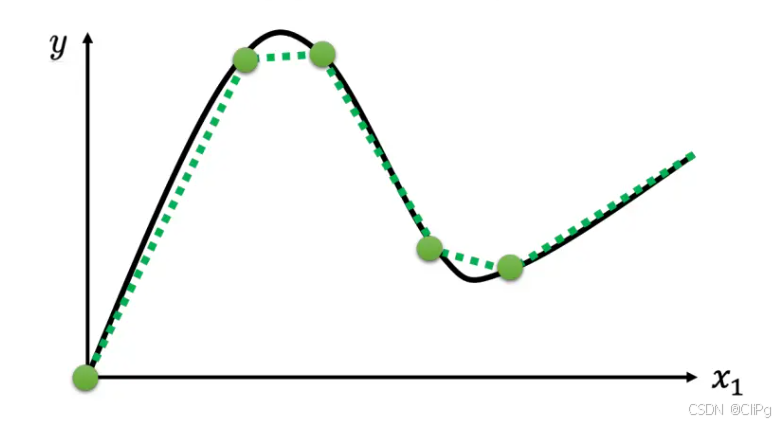
2.4Sigmoid
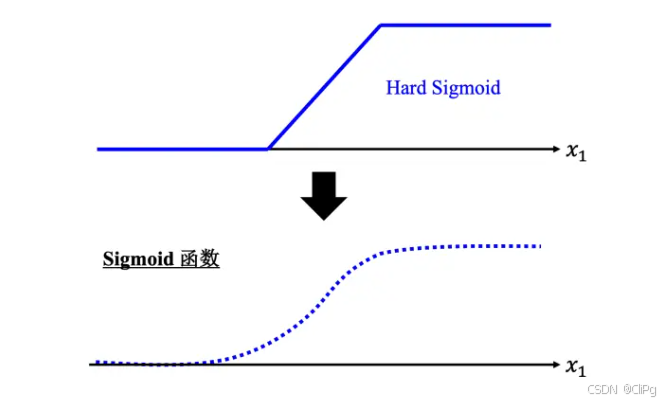
HardSigmoid函数并不是很好写,因此我们可以用Sigmoid函数来逼近
sigmod:
y=c11+e−(b+wx) y = c\frac{1}{1+e^{-(b+wx)}} y=c1+e−(b+wx)1

因此y可以写作
y=b+∑inci11+e−(bi+wix) y = b+ \sum_{i}^{n}c_{i}\frac{1}{1+e^{-(b_{i}+w_{i}x)}} y=b+i∑nci1+e−(bi+wix)1
2.5扩展到多个特征
即由前一天扩展到前j天
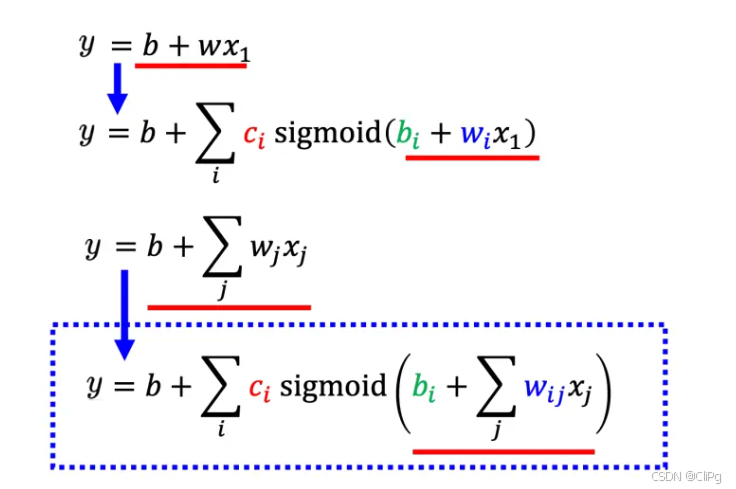
以前三天为例,i表示目标函数由多少个sigmoid函数组成,j表示参考前多少天
r1=b1+w11x1+w12x2+w13x3r2=b2+w21x1+w22x2+w23x3r3=b3+w31x1+w32x2+w33x3 r_{1} = b_{1} + w_{11}x_{1} + w_{12}x_{2} + w_{13}x_{3}\\ r_{2} = b_{2} + w_{21}x_{1} + w_{22}x_{2} + w_{23}x_{3}\\ r_{3} = b_{3} + w_{31}x_{1} + w_{32}x_{2} + w_{33}x_{3} r1=b1+w11x1+w12x2+w13x3r2=b2+w21x1+w22x2+w23x3r3=b3+w31x1+w32x2+w33x3
化为矩阵
[r1r2r3]=[b1b2b3]+[w11 w12 w13w21 w22 w23w31 w32 w33][x1x2x3]
\begin{bmatrix}
r_{1}\\
r_{2}\\
r_{3}
\end{bmatrix}=
\begin{bmatrix}
b_{1}\\
b_{2}\\
b_{3}
\end{bmatrix}+
\begin{bmatrix}
w_{11}\ w_{12}\ w_{13} \\
w_{21}\ w_{22}\ w_{23}\\
w_{31}\ w_{32}\ w_{33}
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2}\\
x_{3}
\end{bmatrix}
r1r2r3=b1b2b3+w11 w12 w13w21 w22 w23w31 w32 w33x1x2x3
即
r=b+Wx
\mathbf{r = b + Wx}
r=b+Wx
令
a=σ(r)
\mathbf{a = \sigma(r)}
a=σ(r)
有
y=b+cTa
y = b + \mathbf{c^{T}a}
y=b+cTa
2.6定义损失
之前是简单的L = L(b,w),而现在有许多参数,因此用 θ\ \theta θ 来代替这些未知参数
因此有 L=L(θ)\ L = L(\theta) L=L(θ)
接着和上面一样,随机选择一组 θ\ \theta θ ,
令
g=▽L(θ)\ \mathbf{g = \bigtriangledown L(\theta)} g=▽L(θ)
然后梯度下降,更新参数
θ1←θ0−ηg\ \mathbf{\theta_{1} \leftarrow \theta_{0} - \eta g} θ1←θ0−ηg
最后停下来,得到让损失最小的一组,称为 θ∗\ \theta ^{*} θ∗
2.7批量与回合
实际使用梯度下降时,并不是利用所有数据生成一个loss,而是把N笔数据随机分成一个一个的批量(batch),每个批量有B笔数据,
每个批量可以得到 L1,L2⋅⋅⋅\ L_{1},L_{2} ··· L1,L2⋅⋅⋅,当B足够大时, L1\ L_{1} L1可能会与 L\ L L接近
对所有批次进行一次梯度下降叫做回合,对某一批进行一次梯度下降叫做更新
2.8模型变形
不一定要把hardsigmoid变成softsigmoid,也可以将其换为两个修正线性单元(ReLU)的加总
ReLU=c∗max(0,b+wx)\ ReLU = c*max(0,b+wx) ReLU=c∗max(0,b+wx)
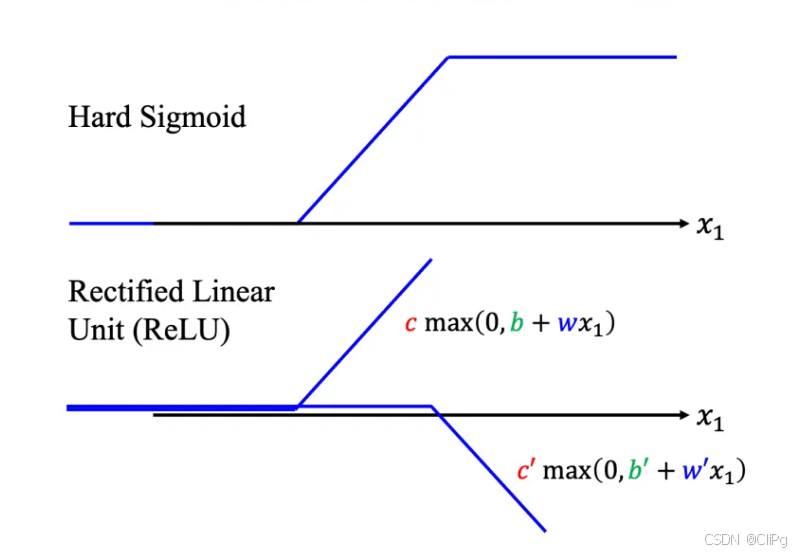
2.8.1激活函数
像sigmoid,ReLU ···
2.9神经网络
2.9.1改进模型
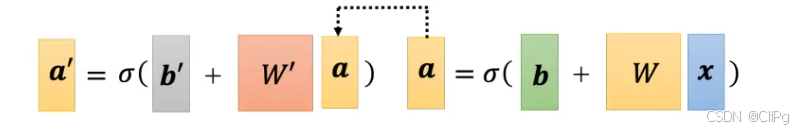
(Q:为什么是把a带到x的位置)
sigmoid或relu称为神经元,很多神经元称为神经网络,每一排称为隐藏层,越叠越深称为深度学习
2.9.2过拟合
模型在训练数据上表现得过于优秀,能够高度拟合训练数据,但在新数据或测试数据上的表现却较差。换句话说,模型在训练过程中过于关注训练数据中的噪声或偶然性模式,从而失去了对新数据的泛化能力。
过拟合可能是因为参数过多或层数过多,但层数过多导致loss过大,并不意味着过拟合,可能是因为优化做的不够。
2.9.2.1一个极端例子
对于训练集的数据,该函数直接输出训练集的数据,而测试集输出随机,尽管训练集loss为0,它仍然是一无是处的函数…
2.9.2.2解决方法
2.9.2.2.1增加训练集
数据增强就是根据问题的理解创造出新的数据。举个例子,在做图像识别的时候,常做的一个招式是,假设训练集里面有某一张图片,把它左右翻转,或者是把它其中一块截出来放大等等。
2.9.2.2.2增加限制
假设x与y的关系是一条二次曲线,在设计模型的时候就可以增加该限制,更有利于得到好的模型。
给模型制造限制可以有如下方法:
- 给模型较少的参数
- 用较少的特征
- 早停、正则化、丢弃法…
但也不能给模型太多限制,这可能会导致模型偏差
Task3
3.实践方法论
3.1模型偏差
假设采用的模型太简单,当你代入很多组 θ\ \theta θ,并且得到了 θ∗\ \theta^{*} θ∗,但这并不意味着找到了足够小的loss,只能称为局部最优解,意味着该模型上限不高,称为模型偏差。
此时可以重新设计一个模型,增大模型弹性,提高模型上限。
3.2优化问题
是并不是训练的时候,损失大就代表一定是模型偏差,可能会遇到另外一个问题:优化做得不好。
一般采用梯度下降进行优化,而这个方法往往会找到局部最小值,而不是全局最小值。
3.2.1残差网络的例子

从中发现56层的loss大于20层,但这并不意味着过拟合,因为56层的灵活性一定比20层大,20层能做到的,56层理应也能做到,这个问题的原因是优化做的不够。
3.2.2易于优化的模型
看到一个从来没有做过的问题,可以先跑一些比较小的、比较浅的网络,或甚至用一些非深度学习的方法,比如线性模型、支持向量机(Support Vector Machine,SVM)
3.3交叉验证
即把训练数据分为训练集和验证集
3.3.1k折交叉验证
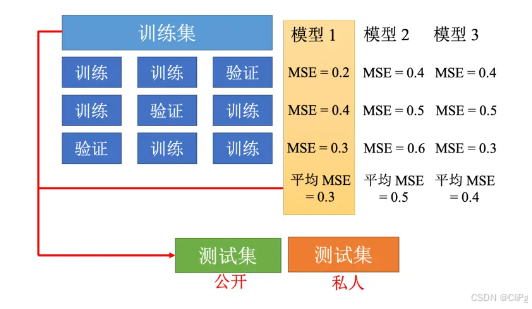
3.3.2不匹配

像这种出现反常点的情况,设计模型的时候,常常会考虑这天是否出现了什么特殊情况(节假日等),从而可以增加特征。




















 2819
2819










