本文深入探讨了动态规划的概念，强调其本质是递推和状态转移，并通过01背包问题的非记忆型递归、记忆型递归及动态规划解法进行详细阐述。此外，还介绍了钢条切割、数字三角形问题的解决方案，以及最长公共子序列问题的双重循环多路分支的DFS解法。最后，讨论了完全背包问题的动态规划算法，展示了如何使用滚动数组优化空间复杂度。
动态规划
1、动态规划代表一类问题（最优子结构或子问题最优解）的一般解法，是设计方法或者策略，不是具体算法。
2、本质是递推，核心是状态转移的方式，写出dp方程。在展开的子问题中存在重叠的情况。
3、形式：记忆型递归 递推
4、01背包问题
有n个重量和价值分别为wi、vi的物品，从这些物品中挑选出总重量不超过W的物品，求所有方案中价值总和的最大值。（一个物品是拿或者不拿：0或者1）
非记忆型递归
//01背包问题
public class Main {
static int n=4;
static int W=5;
static int[] v={3,2,4,2};
static int[] w={2,1,3,2};
public static void main(String[] args) {
int ww=W;
int max=dfs(0,ww);
System.out.print(max);
}
//i是接下来的几号物品供选择
//ww是背包还能承受的重量
private static int dfs(int i,int ww) {
if(ww<=0) {//装不下了
return 0;
}
if(i==n) {//没有可供选择的了
return 0;
}
//不选择当前该号物品,价值不加，重量不减
int v1=dfs(i+1,ww);
//如果还能装下就选择当前该号物品
if(ww-w[i]>=0) {
int v2=v[i]+dfs(i+1,ww-w[i]);//加价值，减重量
return Math.max(v1, v2);//返回价值最大的情况
}
return v1;
}
}
记忆型递归（效率更高）
//01背包问题
public class Main {
static int n=4;
static int W=5;
static int[] v={3,2,4,2};
static int[] w={2,1,3,2};
static int[][] rec=new int[n][W+1];//负责记录
public static void main(String[] args) {
int ww=W;
for(int i=0;i<rec.length;i++) {
for(int j=0;j<rec[i].length;j++) {
rec[i][j]=-1;//对记录数组进行初始化，当查询为-1时说明前面没有处理过
}
}
int max=dfs(0,ww);
System.out.print(max);
}
//i是接下来的几号物品供选择
//ww是背包还能承受的重量
private static int dfs(int i,int ww) {
if(ww<=0) {//装不下了
return 0;
}
if(i==n) {//没有可供选择的了
return 0;
}
//计算前查询
if(rec[i][ww]>=0)//已经查询过了，直接返回之前查询的结果
return rec[i][ww];
int ans;//用于记录结果
//不选择当前该号物品,价值不加，重量不减
int v1=dfs(i+1,ww);
//如果还能装下就选择当前该号物品
if(ww-w[i]>=0) {
int v2=v[i]+dfs(i+1,ww-w[i]);//加价值，减重量
ans= Math.max(v1, v2);//返回价值最大的情况
}else {
ans= v1;
}
//计算后记录
rec[i][ww]=ans;
return ans;
}
}
用dp解法解决背包问题
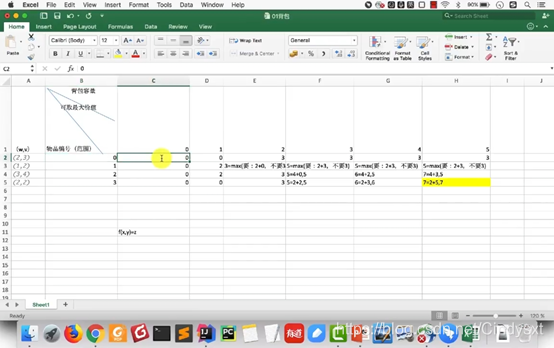
每个编号及其以上编号的物品供选择，当前编号的物品有选和不选两种情况，当选择了当前物品，那么就在上一行表格中找到剩余重量对应单元格的值，加上即为结果；如果不选择当前单元格，那么就直接将正对着的上一行的值移下来。
需要构建一个二维数组来存放之前计算过的值。
能够避免重复求解同一个过程。
//用dp解法解决01背包问题
public class Main {
static int W=5;
static int n=4;
static int[] w= {2,1,3,2};
static int[] v= {3,2,4,2};
static int[][] dp=new int[n][W+1];//用来存放已经计算过的过程的结果
public static void main(String[] args) {
System.out.println(dp());
}
//dp解法
private static int dp() {
//初始化第一行
//遍历第一行的每一列
for(int i=0;i<W+1;i++) {
if(i>=w[0])//能装下
dp[0][i]=v[0];
}
//计算 从第二行开始，第一行已经初始化过了
for(int i=1;i<n;i++) {
for(int j=0;j<W+1;j++) {
//装的下,有两种选择：装或者不装
if(j>=w[i]) {
int i1=v[i]+dp[i-1][j-w[i]];//该物品价值以及剩下重量的价值
int i2=dp[i-1][j];
dp[i][j]=Math.max(i1, i2);
}else {//装不下，只能选择不装
dp[i][j]=dp[i-1][j];//直接取上一行的值
}
}
}
return dp[n-1][W];
}
}
钢条切割
一个公司购买长钢条，将其切割为短钢条出售，切割工序本身没有成本支出。公司管理层希望知道最佳切割方案。假定我们知道该公司出售长为i英寸的钢条价格为pi（i=1,2，……，单位为美元），钢条的成都均为正英寸。给定一段长度为n英寸的钢条和一个价格表pi，求切割钢条的方案，使得销售量rn最大。 注意：如果长度为n英寸的钢条的价格pn足够大，最优解就是完全不需要切割。
思路：递归—记忆型递归—dp （不熟练的话就先递归再dp）先想递归，然后去掉重复。
记忆型递归
public class Main2 {
static int[] v= {1,5,8,16,10,17,17,20,24,30};
static int[] rec=new int[11];//记录已经计算过得情况 下表到10
public static void main(String[] args) {
for(int i=0;i<rec.length;i++) {
rec[i]=-1;
}
System.out.print(r(10));
}
//每次保留一个长度，其他的长度进行最大价值选择
private static int r(int x) {
if(x<=0) {//退出条件
return 0;
}
//计算前检查
if(rec[x]!=-1) {
return rec[x];
}
int ans=0;
for(int i=1;i<=x;i++) {
int v1=v[i-1]+r(x-i);
ans=Math.max(ans, v1);
rec[x]=ans;//计算后记录
}
return ans;
}
}
dp算法解决
public class Main2 {
static int[] v= {1,5,8,16,10,17,17,20,24,30};
static int[] rec=new int[11];//记录已经计算过得情况 下标到10
static int n=10;
public static void main(String[] args) {
for(int i=0;i<rec.length;i++) {
rec[i]=-1;
}
System.out.print(dp());
}
//每次保留一个长度，其他的长度进行最大价值选择
private static int dp() {
rec[0]=0;
for(int i=1;i<=n;i++) {//拥有的链条长度
for(int j=1;j<=i;j++) {//保留j为整段
if(rec[i]<(v[j-1]+rec[i-j])) {//注意下标和序号的对应关系
rec[i]=v[j-1]+rec[i-j];
}
}
}
return rec[n];
}
}
数字三角形
题目描述：在数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步只能往左下或者右下走，只需求出这一最大和即可，不必给出具体路径。
dfs解法
public class Main {
static int[][] triangle= {
{7},
{3,8},
{8,1,0},
{2,7,4,4},
{4,5,2,6,5}
};
public static void main(String[] args) {
System.out.print(dfs(triangle,0,0));
}
//每次保留一个长度，其他的长度进行最大价值选择
private static int dfs(int[][] triangle,int i,int j) {
int rowIndex=triangle.length;
if(i==rowIndex-1) {
return triangle[i][j];
}else {//顶点值加左支路和右支路的最大值
return triangle[i][j]+Math.max(dfs(triangle,i+1,j),dfs(triangle,i+1,j+1));
}
}
}
记忆型递归
public class Main2 {
static int[][] rec=new int[5][5];
static int[][] triangle= {
{7},
{3,8},
{8,1,0},
{2,7,4,4},
{4,5,2,6,5}
};
public static void main(String[] args) {
//初始化记忆数组
for(int i=0;i<rec.length;i++) {
for(int j=0;j<rec[0].length;j++) {
rec[i][j]=-1;
}
}
System.out.print(dfs(0,0));
}
//每次保留一个长度，其他的长度进行最大价值选择
private static int dfs(int i,int j) {
int rowIndex=triangle.length;
if(rec[i][j]!=-1) {
return rec[i][j];
}
if(i==rowIndex-1) {
rec[i][j]=triangle[i][j];
}else {//顶点值加左支路和右支路的最大值
rec[i][j]=triangle[i][j]+Math.max(dfs(i+1,j),dfs(i+1,j+1));
}
return rec[i][j];
}
}
用dp算法解决
思路：由下至上计算，在每一个位置算出最大值
public class Main2 {
static int[][] dp=new int[5][5];
static int[][] triangle= {
{7},
{3,8},
{8,1,0},
{2,7,4,4},
{4,5,2,6,5}
};
public static void main(String[] args) {
//初始化最后一行
for(int i=triangle.length-1;i>=0;i--) {
for(int j=0;j<triangle[i].length;j++) {
dp(i,j);
}
}
System.out.print(dp[0][0]);
}
//每次保留一个长度，其他的长度进行最大价值选择
private static void dp(int i,int j) {
int length=triangle.length;
if(i==length-1) {
dp[i][j]=triangle[i][j];//最后一行的最大值就是它自己
}else {
dp[i][j]=triangle[i][j]+Math.max(dp[i+1][j],dp[i+1][j+1]);//选左右的最大值
}
}
}
dp算法中改用滚动数组
如果前面算的一组数在后面就用不到了就可以进行覆盖。
public class Main2 {
static int[] dp=new int[5];
static int[][] triangle= {
{7},
{3,8},
{8,1,0},
{2,7,4,4},
{4,5,2,6,5}
};
public static void main(String[] args) {
//初始化最后一行
for(int i=triangle.length-1;i>=0;i--) {
for(int j=0;j<triangle[i].length;j++) {
dp(i,j);
}
}
System.out.print(dp[0]);
}
//每次保留一个长度，其他的长度进行最大价值选择
private static void dp(int i,int j) {
int length=triangle.length;//行数
if(i==length-1) {
dp[j]=triangle[i][j];//最后一行的最大值就是它自己
}else {
dp[j]=triangle[i][j]+Math.max(dp[j],dp[j+1]);//选左右的最大值
}
}
}
最长公共子序列
题目描述：求两个字符串的最大公共子序列。例如：AB34C和A1BC2的最大公共子序列为：ABC（注意子序列只要顺序相同即可，子数组则要求连续）
思路：如果暴力的话，就是找出所有的公共子序列，然后挑出最长的。找公共子序列：先找出准备作为开头的那个字符，顺序从其中一个数组中找出准备打头的字符，在另一个数组中找该字符，若找不到就换下一个字符打头；找到的话就在两个数组剩下的部分进行相同的操作。
双重循环多路分支的dfs解法
import java.util.ArrayList;
//最长公共子序列
public class Main2 {
public static void main(String[] args) {
System.out.println(dfs("AB34C","A1BC2"));
System.out.println(dfs("3563243","513141"));
System.out.print(dfs("3069248","513164318"));
}
//求s1和s2的最长公共子序列
private static ArrayList<Character> dfs(String s1,String s2) {
ArrayList<Character> ans=new ArrayList<Character>();//记录最长的结果
for(int i=0;i<s1.length();i++) {//顺序依次以各字符开头
ArrayList<Character> al=new ArrayList<Character>();
for(int j=0;j<s2.length();j++) {//在s2中找相同的字符
if(s1.charAt(i)==s2.charAt(j)) {//如果找到的话
al.add(s1.charAt(i));//将该字符添加到链表里面
al.addAll(dfs(s1.substring(i+1),s2.substring(j+1)));
break;//只需要找到这一个就行了
}
}
if(al.size()>ans.size()) {
ans=al;
}
}
return ans;
}
}
完全背包问题
题目描述：不限制物品的个数，即一种物品可以拿多个。有n个重量和价值分别为wi，vi的物品，从这些物品中挑选出总重量不超过W的物品，使它们的价值总和最大。
解题思路：跟01背包问题比较相似，但是在决定选当前该物品后，剩下的重量要在同一行找对应的最大价值，而不是从上一行找对应的最大价值。
用dp算法解决
//完全背包问题,每个包裹的个数不限
//选或不选当前的物品 然后剩下的价值带当前行寻找对应值
public class Main2 {
static int[] w= {2,1,3,2};//重量
static int[] v= {3,2,4,2};//对应价值
static int n=4;
static int W=10;//总重量
static int[][] rec=new int[4][11];//用来记录各阶段计算的值
public static void main(String[] args) {
//初始化
for(int i=0;i<rec[0].length;i++) {
if(i>=v[0]) {
rec[0][i]=v[0]+rec[0][i-v[0]];
}
}
System.out.print(dp());
}
private static int dp() {
for(int i=1;i<n;i++) {
for(int j=0;j<=W;j++) {
if(j>=v[i]) {//要得起
int v1=v[i]+rec[i][j-v[i]];//要该物品
int v2=rec[i-1][j];//不要该物品
rec[i][j]=Math.max(v1, v2);
}else {//装不下的情况
rec[i][j]=rec[i-1][j];
}
}
}
return rec[n-1][W];
}
}
扫一扫
4万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
