2020年2月19日12:54:18
导数、偏导数、方向导数、梯度
- 导数,指的是一元函数中,函数y=f(x)在某一点处沿x轴正方向的变化率;
- 偏导数,指的是多元函数中,函数y=f(x1,x2,…,xn)在某一点处沿某一坐标轴(x1,x2,…,xn)正方向的变化率。
- 方向导数, 某一点在某一趋近方向上的导数值。
- 梯度,函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
梯度的提出只为回答一个问题:
函数在变量空间的某一点处,沿着哪一个方向有最大的变化率?
(eg.三维曲面上某一点处有不同的方向,每个方向对应一个方向导数,而这个最大的方向导数就是梯度的值,此时的方向就是梯度的方向。)
只有梯度是向量。
梯度下降法

可以理解为,每一个变量要以step_size的速度朝着梯度的反方向变化。
以下是原理解释:
原作者: 红色石头|来自: AI有道
梯度的反方向即是函数在该点处下降最快的方向。
一阶泰勒展开式
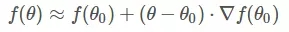

梯度下降数学原理

想要两个向量的乘积小于零,我们先来看一下两个向量乘积包含哪几种情况:

A和B均为向量,α为两个向量之间的夹角。A和B的乘积为:








 本文深入探讨了导数、偏导数、方向导数及梯度的概念,解释了它们在数学中的作用,并详细介绍了梯度下降法的原理及其在求解函数最优化问题中的应用。
本文深入探讨了导数、偏导数、方向导数及梯度的概念,解释了它们在数学中的作用,并详细介绍了梯度下降法的原理及其在求解函数最优化问题中的应用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








