机器学习笔记之分类算法（一）逻辑回归

1. 线性回归和逻辑回归（LR）

线性回归可以很好的解决回归问题，但是针对分类问题效果不佳。因为线性回归的输出值是不确定范围的，无法很好的一一对应到若干分类中。

为了解决上述问题，逻辑回归诞生了。通过在线性回归模型中引入Sigmoid函数，将线性回归的不确定范围的连续输出值映射到（0，1）范围内，成为一个概率预测问题。

线性回归
逻辑回归

sigmoid函数：

为什么采用sigmoid函数：
1）可以将结果映射到（0，1）之间，转化为概率问题；
2）方便进行决策，当x=0时，sigmoid函数值为1/2；
3）求导容易。

2. 最大似然估计

最大似然估计是指整体概率分布已知，利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的分布模型的参数值。

最大似然估计的过程：

1）首先要知道整体的分布模型，比如随便一个分布，概率密度p(x)，参数是θ
2）其次要有一些样本数据，假设为D

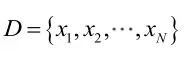
3）似然函数就是样本D同时发生的联合概率密度，定义为L，自变量是θ

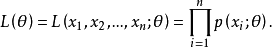
4）当未知参数只有一个时，我们可以对L求导，令导数为0取极值，解出θ。

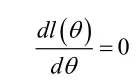
5）当未知参数有多个时，我们可以对L求偏导，令偏导数为0，得到方程组解出参数。

3. 损失函数

线性回归的损失函数对逻辑回归不可用，因为逻辑回归的值是0或1，求距离平均值会是一条不断弯曲的曲线，不是理想的凸函数。

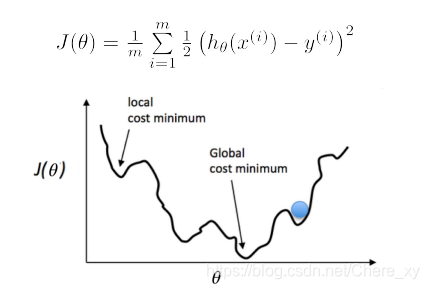
因此，我们换一个思路，用到最大似然估计，根据假设函数构造一个它的分布的概率密度，利用已知的样本反推参数。
假设函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

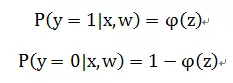
我们将这2个式子合并，得到概率公式：

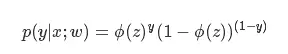
由最大似然估计可知，联合概率就是：

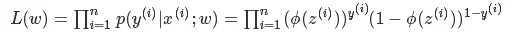
为了简化计算，我们对L(w)取对数：

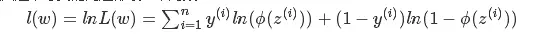
最后得到代价函数：

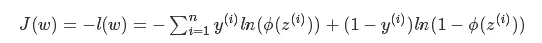
4. 参数求解

和线性回归类似，可以使用梯度下降算法来求解参数。

5. 适用场景

逻辑回归适用于二分类问题，实际工作中，我们可能会遇到如下问题：

1）预测一个用户是否点击特定的商品；
2）判断用户的性别；
3）预测用户是否会购买给定的品类；
4）判断一条评论是正面的还是负面的；

这些都可以尝试使用逻辑回归算法。

6. 优点

1. 它直接对分类可能性进行建模，无需事先假设数据分布，这样就避免了假设分布不准确所带来的问题；
2. 它不是仅预测出“类别”，而是可以得到近似概率预测，这对许多需利用概率辅助决策的任务很有用；
3. 对率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可以直接用于求取最优解。