DES算法总结

DES算法总结

下文中所指的教材均指：清华大学李辉老师的《计算机安全与保密》

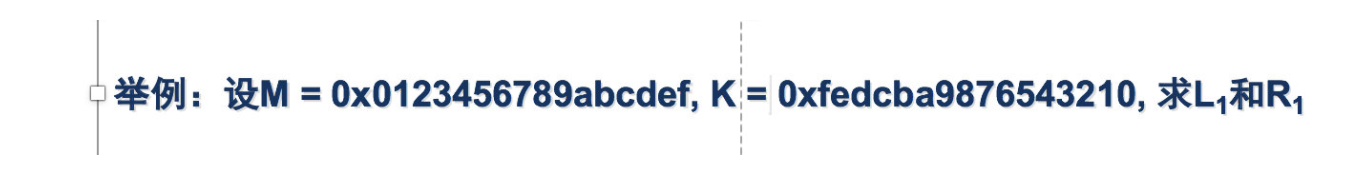
题目中的M即为明文，K为初始密钥。

要求L1和R1

1.将M写成二进制的形式

M一共包含16个十六进制位，写成二进制一行肯定写不下，

所以我们分8行写，每一行只对应两个十六进制位。

2.对二进制M进行初始IP变换

这就是个换位变换，具体查阅教材31 表2.4 是个8x8矩阵。

索引是从1开始的。

ip变换表跟我们的二进制矩阵的形式是类似的,都是8x8矩阵。

第一个数58,意思就是将明文中的第58个二进制位放到该位置来。

第二个数50,意思就是将明文中的第50个二进制位放到该位置来。

这样一来，我们就得到了一个新的二进制矩阵。这就是初始变换后的明文

我们记为x0

$x_0=L_0{R}_0$

所以这个二进制矩阵的前半部分(即上半部分)就是$L_0$

下半部分就是$R_0$

3.迭代运算

$L_1=R_0$

这样L1就求出来了。

$R_1=L_0⨁f(R_0,k_1)$

L0已知，R0已知 ,现在就是k1未知。但是我们知道初始密钥k

下面我们要根据密钥生成算法求出k1才行。

4. 将初始密钥K写成二进制的形式

跟M一样，我们也将k写成8x8的二进制矩阵形式，主要是为了便于后续的运算。

5.换位选择1得56位密钥

初始密钥K一共64位，现在我们要将他变成56位。

具体查教材34页 表2.11

换位选择1的表一共56位，是8x7的矩阵。

第一个元素57的意思是：将初始密钥二进制串的第56位放到这个位置。

第二个元素49的意思是：将初始密钥二进制传的第49位放到这个位置。

看这个表是在是太累了，你直接按照这个顺序从初始密钥二进制矩阵中抄就好了。

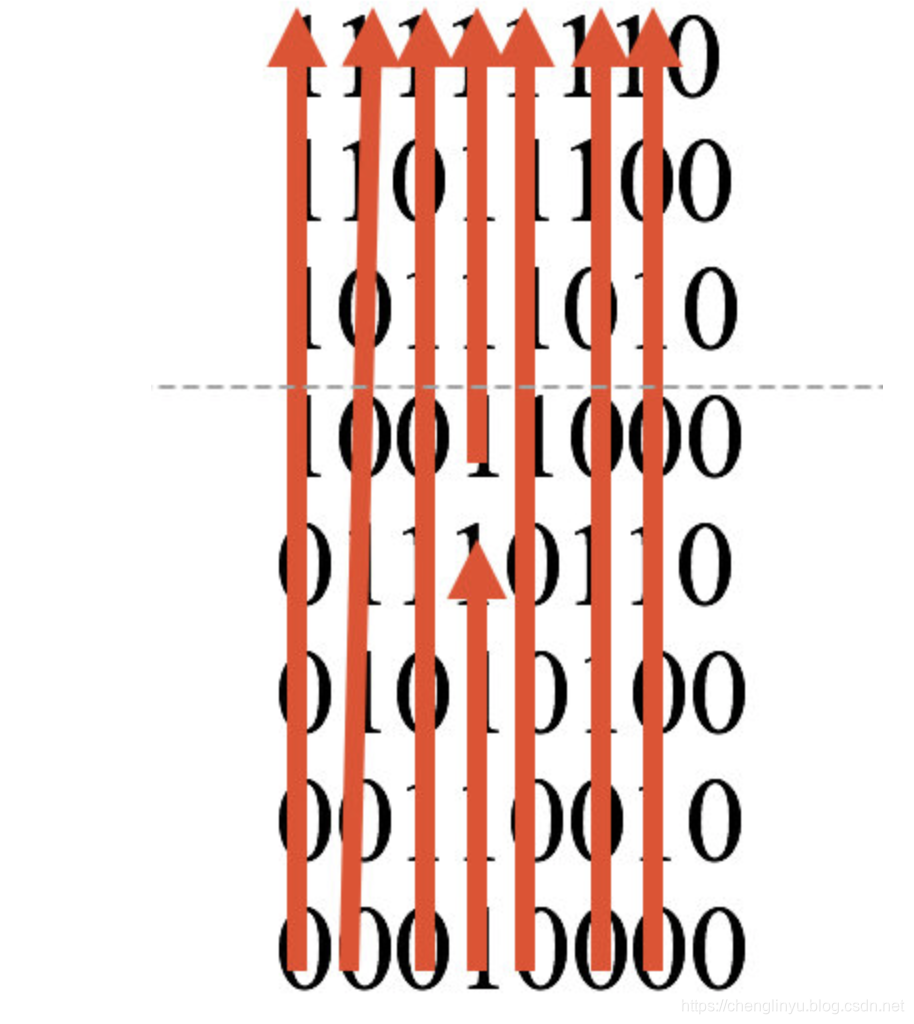
先从左下角开始抄，每行抄8位，抄完之后就抄了28位了，这就是C(0)

然后再从右下角开始抄，接着之前的28位写，每行8位。这就是D(0)

接下来的操作就是分别对C(0)和D(0)进行操作了。

这样就得到了一个7行，8列的矩阵。

6.分别对C(0)和D(0)进行左移位

$C(1)=\lambda \sigma (1)C(0)$

$D(1)=\lambda \sigma (1)D(0)$

$\lambda \sigma (i)$是个移动位置的函数

查教材34页表2.1可知(不用查了)$\lambda \sigma (1)=1$

所以分别将C(0)和C(1)向左移动一位就可以了。

C(0)循环左移得到C(1)

D(0)循环左移得到D(1)

C(1)和D(1)拼接起来，接着做下面的操作

7.对拼接之后的C(1)D(1)进行换位选择2得到k1

查教材34页表2.13，换位选择2的表是8x6的矩阵，所以我们最终的k1也是8x6的。

换位选择2没有什么规律，一个一个慢慢抄吧，

结果就是K1，

8.根据第3步的迭代运算

$R_1=L_0⨁f(R_0,k_1)$

需要计算$f(R_0,k_1)$

$R_0$是8x4 = 32位的，$k_1$是8x6= 48位的。

8.1 先对$R_0$进行扩展得E($R_0$)

查阅32页表2.6

原来的$R_0$不动，直接在两边扩展。

左边扩展一位，右边扩展一位。

得到一个8x6的矩阵$E(R_0)$。和k1相同

8.2 将$E(R_0)$和k1异或

两个矩阵做异或你会吧。

得到一个8x6的矩阵。

8.3 进行S盒代替

查阅32页表2.7

每一行对应一个s盒子

第1行对应s(1)

第2行对应s(2)

每一行从6位变成了4位。

所以得到一个8x4的矩阵

8.4 经过一个换位变换

查阅教材33页表2.8

注意这个表是先看左半边，再看右半边。

注意第2行开头的29是第5位。

表示新二进制位的第5位是原来二进制串的第29位

---

至此就得到了$ f(R_{0},k_1)$

L0是个4x8的矩阵。所以我们要做异或的话需要将刚刚得到的8x4

矩阵也写成4x8矩阵，两行并成一行就好了，OK！得到的就是R1

$R_1=L_0⨁f(R_0,k_1)$