dataframe和list是我们在R中常见的两种数据结构,也许我们经常使用,但如果到了我们需要存储数据或者构建数据的结构时,不清楚其中的区别,很容易在后续的数据处理中吃亏。
dataframe(数据框)
在日常使用中,我们一般可以将其理解为跟excel有相同的作用,可以存储一列列数据,且存入的每一列数据的行数都是一致的。这并不是说如果存入不同长度的数据时代码会报错,相反,其会自动把每一列的长度补充到跟最长列相同,用NA填入空出的地方。这就会导致我们很难发现数据之间的不同,尤其是在我们尝试将数据合并的时候,很容易忽略这种细节。
当然了,dataframe的好处也很明显,当我们读入或对其进行操作时,由于其结构的简单,R的响应效率很快,尤其是在读入大数据时,会帮我们节省不少时间,所以很多时候,如果只是单独要对一个列表下的一个子列表操作,我们可以单独将其提出来并转为dataframe格式:
test <- lab$test
test<- test$test
列表(list)
与dataframe不同,存储在list的数据不要求长度相同,可以存储任意一种数据,甚至可以嵌套很多个子列表在其中,所以我们一般看到的很多数据,都是以list的形式存储的,经拷出来后,再经由操作把数据拿出来处理。所以其存储自由度带来的,就是其所占用的内存比较多,在用Rstudio读取list数据时需要花费很多时间,也会占用很多运行内存,一不小心处理不当,就要重新读数据,很麻烦。(所以一般读取完list,操作完数据后,会把数据以dataframe的形式存起来,方便回溯)。
聚类分析(Clustering Analysis)
聚类分析是一种将相似的数据点分组(聚类)的方法,常用于数据探索、市场细分、图像分析等场景。简单来说,就是将相似的数据点分到同一组,以K-means举例,其原理是随机选取K个中心点,计算每个点到中心点的距离,将距离相近的分到同一组,并不断地重复选中心点(取组内平均值)和计算距离再分组这个流程,直到中心点不再变化。
下面我们用代码来演示这一过程:
# library
library(tidyverse)
library(ggplot2)
set.seed(123) # 确保结果可重复
class1 <- data.frame(
X1 = rnorm(20, mean = 2, sd = 0.3),
X2 = rnorm(20, mean = 2, sd = 0.3), # X2 也分离
TrueClass = "Class1"
)
class2 <- data.frame(
X1 = rnorm(20, mean = 6, sd = 0.3),
X2 = rnorm(20, mean = 6, sd = 0.3),
TrueClass = "Class2"
)
class3 <- data.frame(
X1 = rnorm(20, mean = 2, sd = 0.3),
X2 = rnorm(20, mean = 6, sd = 0.3),
TrueClass = "Class3"
)
# 合并所有数据
sim_data <- rbind(class1, class2, class3)
# 2. 运行 K-Means 聚类(K=3)
kmeans_result <- kmeans(sim_data[, c("X1", "X2")], centers = 3)
print(kmeans_result$centers) # 聚类中心
table(sim_data$TrueClass, kmeans_result$cluster) # 对比真实类别
# 添加聚类标签到数据
sim_data$Cluster <- as.factor(kmeans_result$cluster)
# 绘制散点图(颜色=聚类结果,形状=真实类别)
ggplot(sim_data, aes(X1, X2, color = Cluster, shape = TrueClass)) +
geom_point(size = 3, alpha = 0.8) +
geom_point(data = as.data.frame(kmeans_result$centers),
aes(X1, X2), color = "black", size = 5, shape = 8) +
labs(title = "K-Means 聚类结果 (K=3)",
subtitle = "黑色星号★表示聚类中心") +
theme_minimal()
输出为:
X1 X2
1 2.007536 1.941458
2 6.053012 6.009603
3 1.965837 5.968475
1 2 3
Class1 20 0 0
Class2 0 20 0
Class3 0 0 20
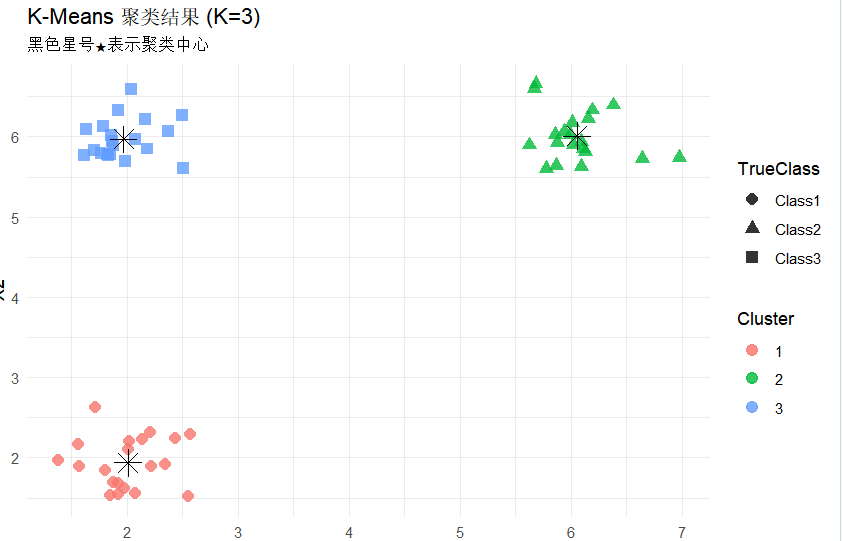
当然了,这是我随机生成的数据,即便是这样,依然调整了才让K-means筛选过的中心点符合数据特点,这说明在实际应用中,我们往往需要先观察数据特点再用方法(例如直接打印散点图)。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








