从0开始学习机器学习--Day12--初识神经网络

神经网络算法解决高特征量学习问题

最新推荐文章于 2025-11-24 19:50:57 发布

原创最新推荐文章于 2025-11-24 19:50:57 发布 · 717 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #学习 #神经网络

非线性假设(Non-linear hypotheses)

在之前所遇到过的学习问题中，所看到的特征量基本都是两到三个，所以我们在处理问题的时候可以很轻易地通过逻辑回归或者线性回归来解决问题，但当特征量多起来的时候，可能单纯地分离正负样本都是一件很难的事。如下是一张非线性假设的图，假如，只有 $x_{1},x_{2}$ 两个特征，我们可以通过逻辑回归，构建有多个二次项的假设函数来解决它，如下：

非线性分类问题的数据点以及假设函数

但如果特征量有很多（例如100），那我们的多项式可能要去到10000个，既不能较少特征量来简化模型，这会丢失很多重要信息，又不能直接计算，这会让特征空间急剧膨胀，且多分类需要每个特征函量都有一个假设函数，工作量很大，这对我们来说是进退两难。

而对于许多实际的机器学习问题来说，特征个数是很大的，我们举一个计算机视觉的例子来说明这个。假设我们想要通过使用机器学习算法来训练一个分类器，使其可以检测图像来判断图像是否是一辆汽车。与人类评价肉眼判断图像不同的是，实际上在计算机的视角里，他们看到的是一个很大的像素点亮度矩阵，这里截取一小部分，如下：

计算机视角里汽车图像的像素点亮度矩阵

通过图片里这个矩阵的一个个亮度数值，计算机才能判断出这代表着一个汽车的门把手。而在实际解决这种问题时，我们往往是提供一个带标签的数样本集，其中一部分样本是各类汽车，而另一部分则不是汽车。将这个样本集输入给算法来训练处一个分类器，然后再通过提供一张新的图片来测试分类器的准确性。

假如我们在图像上截取两个区域，通过其像素强度，也就是那个区域的亮度来在坐标系上标点，将不同的照片在坐标系上标出来，通过正负号来区分是否是汽车，画出来的图就是这样：

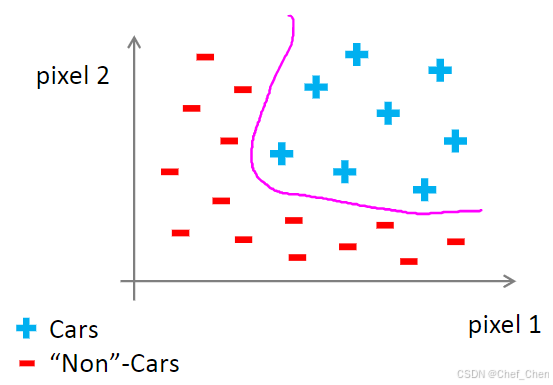
汽车样本集中的数据点分布

假设每张图片是50×50的像素，一个特征量的空间就是2500个像素点，这还只是黑白照片，如果是彩色图片，还要在此基础上乘3。仅仅只是黑白照片，我们就要需要 $(x_{i}\times x_{j})$ 大概3百万个特征。这个数量对于我们来说实在是有点太大了，极大地提高了运算的成本。基于此，神经网络算法应运而生。在讨论神经网络如何运用前，我们先来了解一下神经网络的背景知识，方便我们更好地去理解它。

神经元与大脑(Neurons and the brain)

神经网络的起源来自于人们想尝试设计出模仿大脑的算法，这个想法的理念是，如果我们想要建立一个学习系统来解决问题，那么最好的模仿对象就是人类的大脑，这是我们所认识的最神奇的学习机器。但模仿大脑是不是意味着要写成千上万个软件来实现大脑所学会的各种技能呢？关键就在于“学会”二字。既然大脑是通过学习来获取技能，那么我们设计来模仿大脑的学习系统理论上也只需要一个学习算法就能实现这些功能了。

实际上，生物学家们通过在动物身上做实验发现，如果将听觉或者触觉的神经皮层的神经切断，转而连接视觉的神经，那么被切断的皮层最终能够处理眼睛所带来的信息，也就是学会了“看”，这进一步说明模仿大脑最关键的是找到或设计出一个学习算法。这也说明了另一个现象：似乎只要来自于外界的信号被身体感知到并通过类似传感器的神经将其传输给大脑，大脑就会试着去处理信号，尝试去定义和解读它。基于此，科学家发明了许多帮助残障人士的机器，像人体声呐、触觉皮带还有BrainPort都能让失明的人能够对外界的信号作出处理，从而能尝试像正常人一样去安全地走路。

模型展示I(Model representation I)

神经网络的设计，跟大脑神经元之间信息的传递方式一致，都是通过树突，输入通道来接受一定数目的信息并作相关的计算，再通过轴突传递给其他节点，不同神经元之间通过发出微弱的电流通过输出通道传递信息给下一个神经元，下面我们来看看人工的神经网络是怎样的。

在了解之前，我们需要知道，在人工神经网络中，我们通常只会画出三个输入： $x_{1},x_{2},x_{3}$ ， $x_{0}$ 被称为偏置单元或偏置神经元，由于其一直等于1，我们一般会省略不画。而在逻辑回归中的 $g(z)$ ， $\theta$ 一般还是叫做参数，有时候会在神经网络的有关文献中看到其被称为权重。

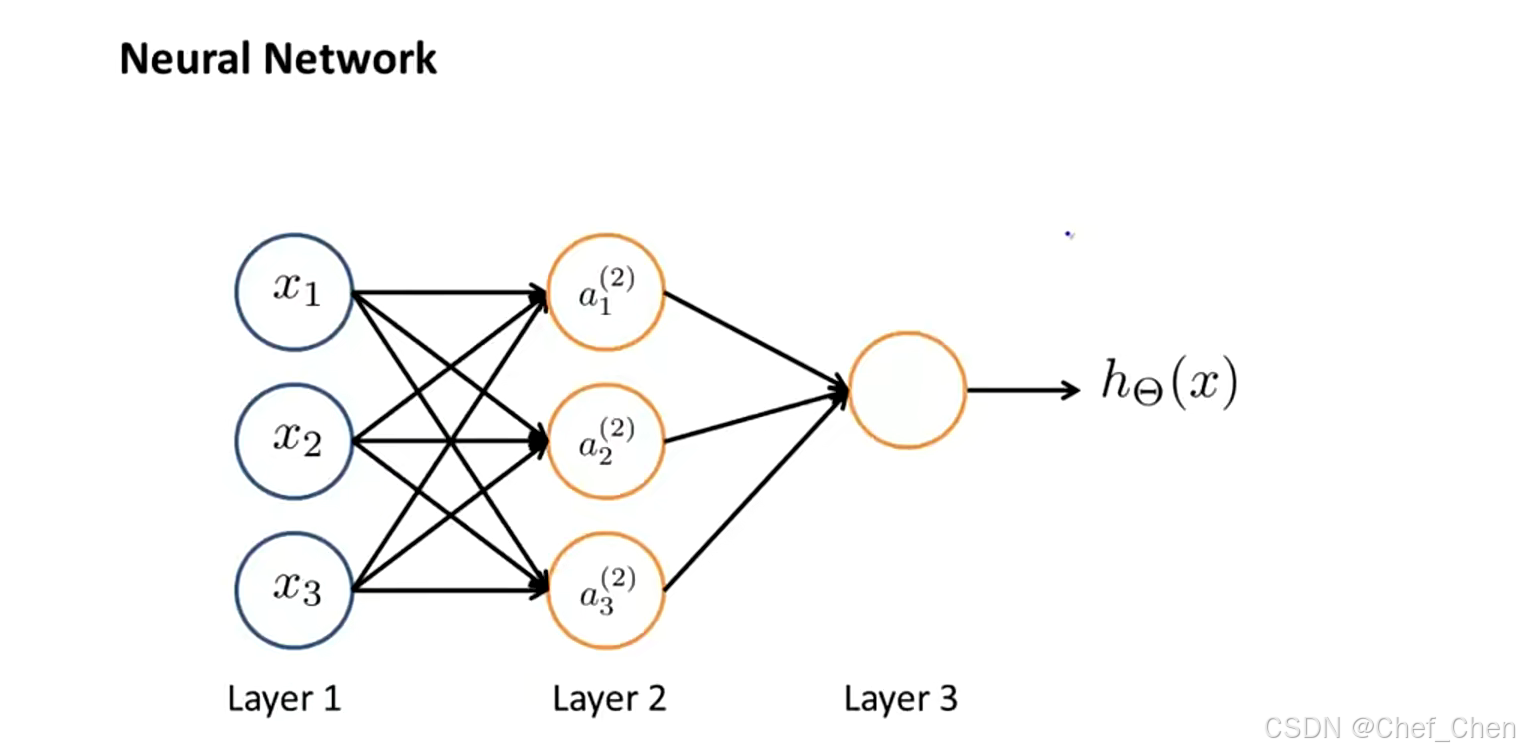
神经网络示意图

如上图所示，神经网络就是一组神经元连接在一起的集合。通常来说，神经网络分为三层，分别是输入层、隐藏层（由于在计算的过程中我们只看到输入和输出的值，中间这层计算得出的值我们是看不到的，故将其成为隐藏层，通常来说神经网络可以有不止一个隐藏层）和输出层。在神经网络中，用 $a_{i}^{j}$ 来表示第j层第i个神经元或单元的激活项，激活项的意思是有一个具体的神经元计算并输出的值， $\theta_{j}$ 代表权重矩阵，控制着第j层和j+1层之间的映射。下图是每个激活项的计算过程以及假设函数的表达：

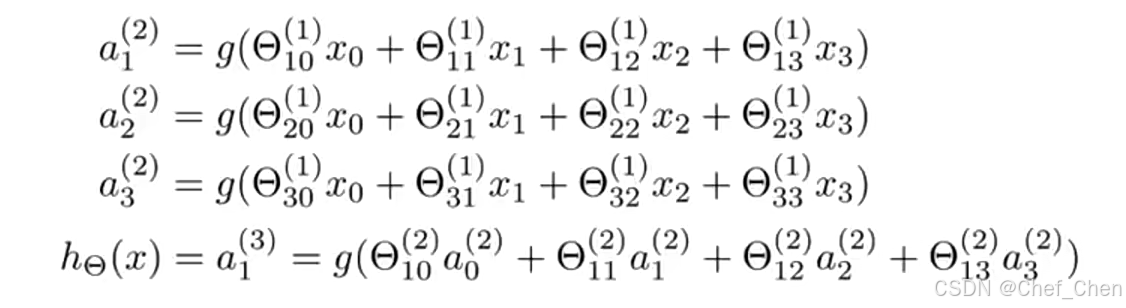
激活项和假设函数的表达

其实这里的表达，简单理解来说就是把每一层的一个神经元都当做一个小的假设函数通过作 $g(\theta^{T}X)$ 的运算得来的。注意这里的 $\theta^{j}$ 的维度计算和之前理解的不太一样，假设j层有 $s_{j}$ 个神经元，j+1层有 $s_{j+1}$ 个，则权重矩阵 $\theta^{j}$ 的维度为 $s_{j+1}\times (s_{j}+1)$ 。

模型展示II(Model representation II)

在上面我们说到可以把每个神经元的输出都当做一个小的假设函数，那么我们不妨设 $z^{(2)}=\begin{bmatrix} z_{1}^{(2)} \\ z_{2}^{(2)} \\ z_{3}^{(2)} \end{bmatrix}$ ，其中每一个 $z_{i}^{j}$ 代表的是第j层第i个激活项的输出，从而我们能写出 $z^{(2)}=\theta^{(1)}a^{(1)}$ ， $a^{2}=g(z^{(2)})$ ， $a^{(1)}$ 其实就是之前的输入，只是为了统一形式写成了这样。注意这里的 $a^{(2)}$ 是四维的，里面还有一个偏置单元 $a_{0}^{(2)}=1$ 。我们把这样计算 $h(x)$ 的过程称之为前向传播，意思是从输入单元的激活项开始，进行前向传播给隐藏层的激活项，再计算输出层的激活项从而得出函数的结果。

假如我们遮住输入层，单看隐藏层和输出层的话，这很像是通过输出层这个逻辑回归节点来预测 $h(x)$ 的值，只是区别在于不是直接输入特征量，而是通过隐藏层的激活项计算后再输入的新的特征量。换句话来说，就是进行了两次逻辑回归，多筛选了一次参数可以获得更好的假设函数，这可以帮助我们得到更多关于模型的信息。

学习内容来自于b站吴恩达大佬课程：https://www.bilibili.com/video/BV1By4y1J7A5?spm_id_from=333.788.player.switch&vd_source=867b8ecbd62561f6cb9b4a83a368f691&p=1