从0开始机器学习--Day6--逻辑回归自己决策界限

原创已于 2024-10-29 21:31:01 修改 · 745 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能

于 2024-10-26 19:07:18 首次发布

假设陈述（Hypothesis representation）

在上一篇的最后，我们提到想要解决分类问题，我们想要函数的输出保持在[0,1]里，为了解决这个问题，我们提出一个假设函数： $h_{\theta}(x)=g(\theta^{T}x)$ ，其中将 $g$ 函数定义为：如果 $z$ 是一个实数，那么 $g(z)=\frac{1}{1+e^{-z}}$ ，这个函数就叫做sigmoid函数或logistic函数，将其带入到假设函数中，我们会得到： $h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T}x}}$ ，而 $g$ 函数图像如下图所示：

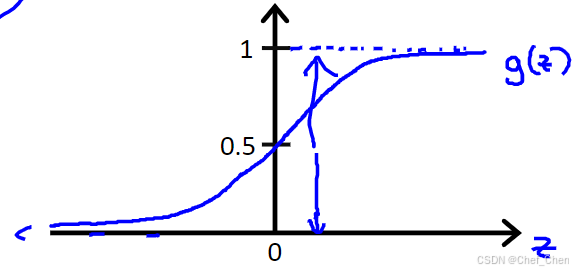
$g$ 函数图像

如图，我们可以观察到图像是一条过点(0,0.5)的曲线，最重要的是，他有我们想要应用在分类问题上的输出：他的 $y$ 值始终在(0,1)之间。

回到之间所说的肿瘤问题，假设我们将一个特征量x喂给我们的假设函数，即 $\begin{bmatrix} x_{0}\\ x_{1} \end{bmatrix} = \begin{bmatrix} 1 \\ tumorSize \end{bmatrix}$ ，假设输出是0.7，这就代表输入了这个肿瘤的信息之后，函数告诉我们这个肿瘤有70%的可能性是恶性肿瘤。如果用概率的方式来表达则是 $h_{\theta}(x)=P(y=1|x;\theta)$ ，意思是在给定 $x$ 的条件下 $y=1$ 的概率，概率的参数是 $\theta$ 。由于 $y$ 的值只可能是0或1，所以 $P(y=0|x;\theta)=1-P(y=1|x;\theta)$ 。

决策界限（Decision boundary）

对于上面提到的假设函数，我们把其分成两种情况可能以便我们对 $y$ 值进行预测：若 $h_{\theta}(x)\geq0.5$ ，认为 $y$ 更有可能偏向1而不是0；反之若 $h_{\theta}(x)<0.5$ ，则认为其更偏向0。但问题的关键在于，什么时候 $h_{\theta}(x)\geq0.5$ 呢？

从 $g$ 函数的图像我们可以看到，当 $z\geq0$ ， $g(z)\geq0.5$ ，也就意味着只要 $\theta^{T}x\geq0$ ，就能满足我们所说的 $h_{\theta}(x)\geq0.5$ ，从而预测 $y=1$ 。类似的，当 $\theta^{T}x<0$ 时，我们也能预测到 $y=0$ 。

假设我们有这样一个已经拟合好的数据集，他满足假设函数 $h_{\theta}(x)=g(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2})$ ，拟合后的参数 $\theta = \begin{bmatrix} -3\\ 1 \\ 1 \end{bmatrix}$ ，那么按照我们上面所说，只要满足 $-3+x_{1}+x_{2}\geq0$ ，就能得到 $y=1$ 的预测值。也就是说，我们画出训练集的坐标图，以 $x_{1}+x_{2}=3$ 为分界线，在线的右边便是满足条件的点，而这条线也就被叫做决策边界，如图：

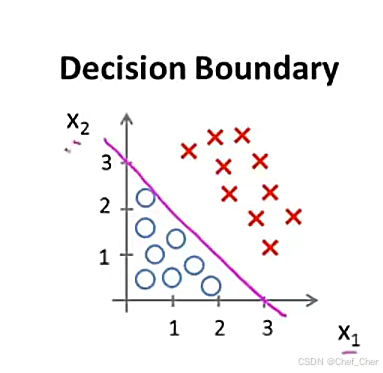
将正负样本通过决策边界划分出来

需要注意的是，决策边界是由假设函数的参数决定的，与数据集本身无关，即使去掉了这些数据点，决策边界以及划分的区域依然存在。

我们接着来看一个更复杂的例子，还是跟之前一样用×代表证样本，圆圈代表负样本，横坐标轴是 $x_{1}$ ，纵坐标轴是 $x_{2}$ ，如图：

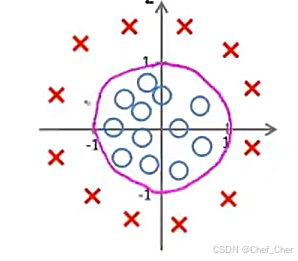
复杂函数的决策边界

其假设函数为 $h_{\theta}(x)=g(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\theta_{3}x_{1}^{2}+\theta_{4}x_{2}^{2})$ ，假设我们已经使用某种算法去拟合，得到的参数 $\theta=\begin{bmatrix} -1 \\ 0 \\ 0 \\ 1 \\ 1 \end{bmatrix}$ ，，也就是说当 $x_{1}^{2}+x_{2}^{2}\geq1$ ，预测值 $y=1$ ，显然，这个直线的意义便是取圆心为原点，半径为1的圆线上及圆以外的点，其预测值 $y=1$ 。