从0开始学习机器学习--Day5--作业总结及初步了解分类问题

吴恩达第一次机器学习作业反思及经验：

尽管学了梯度下降以及正规方程，解决线性回归仍是运用sklearn的线性回归模型解决，而通过用梯度下降去解决，更深刻地认识到了之前视频所学的参数定义，代价函数推导、必要的操作（归一化、数据转化成矩阵、向量的形式等等）以及在运用过程中各种严格的定义，而且老师所讲的各种限制以及过程中涉及到的矩阵、向量和函数的关系都有所体现，希望在下次作业中先试着先用梯度下降或者正规方程去解决。

矢量(Vectorization)

在写代码的过程中，将变量通过库来矢量化可以简化代码，让其看起来不那么冗杂的同时跑起来更加顺畅。

例如之前的假设函数，可以写成，的形式，前者是一系列数据的和，后者是两个向量相乘，体现在代码上则是：

相同函数用不同代码表达

类似的，我们也能将梯度下降公式转化为向量与向量之间的运算，再结合成矩阵，继而推导出 ,详细推导请看上一篇文章末尾链接。

分类（Classification）

提到分类问题，像之前说的垃圾邮件、网络上的欺诈性新闻以及肿瘤的好坏，尝试预测变量y都可以有两个取值的变量0或1，0叫做负类，1叫做正类。把哪类结果分成1都可以，但一般会把要寻找的那一类归为1，如良性肿瘤，垃圾邮件等等。

加入给出一个肿瘤的训练集，把之前学过的线性回归算法应用在这个数据集上，用直线对数据进行拟合，可能会得到这样的一条直线，如下：

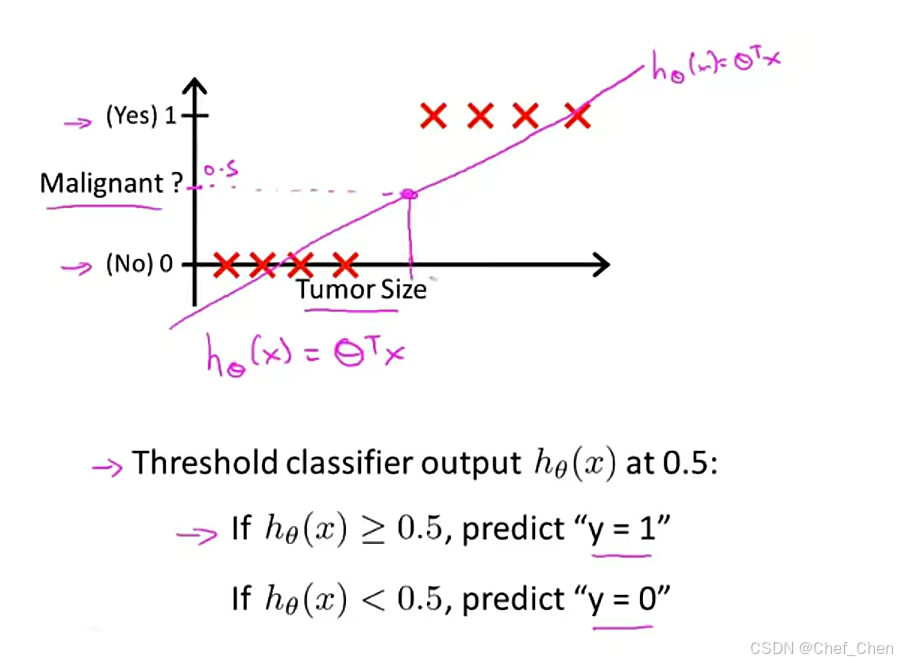
用线性回归拟合分类问题

在这种情况中，由于数据看起来分布较均匀，线性回归的结果是通过0.5将其分成了两类，但如果把横轴拉长，且发现有一个点出现在一个很远的地方呢？这样会得到另一条直线，此时作为分界线的点也被迫拉到右边，此时得到的结果就跟之前不一样了：模型为了将右边的点纳入1，而被迫将左边的点归入到了0，这显然不符合我们的预期。

由此，我们提出一个分类算法：logistics回归算法，可以使得输出值始终在[0,1]之间，从而可以在将所有结果进行分类的同时不改变原本结果的分类。

学习内容来自于b站吴恩达大佬课程：https://www.bilibili.com/video/BV1By4y1J7A5?spm_id_from=333.788.player.switch&vd_source=867b8ecbd62561f6cb9b4a83a368f691&p=1