【S9-分支限界】

前言

分支限界法与回溯法类似，都是在解空间树中寻找问题解的算法。
两者本质区别在于搜索策略即结点生成次序不同：

• 回溯：当前E-结点生成任一个儿子结点后，该儿子结点立即成为新的E结点，深度优先次序。
• 分支限界：当前E-结点生成所有儿子结点后，再生成其他活结点的儿子结点且借助限界函数避免生成不包含答案结点子树的状态空间，广度优先（FIFO 队列实现）、D-检索（LIFO 堆栈实现）、LC-检索。
  分支限界法搜索答案节点步骤：

9.1.1 LC-检索

定义：用成本估计函数来选择下一个E结点的检索策略。

LC检索的提出：

成本函数c(X):
得到成本函数常常是比较困难的，所以采用估计函数g(X)来代替成本函数。
估计函数g(X):
用来估计由X到达一个答案节点所需要的成本。

而仅考虑估计函数g(X)则会导致检索偏向于纵向检索，因此不仅考虑结点X到一个答案结点的估计成本值ĝ(X)，还应考虑由根结点到结点X的成本h(X)
即：ĉ(X)=f(h(X))+ĝ(X)其中，f(.)是一个非降函数，不妨将f的作用理解为调整h和ĝ在成本估计函数ĉ中的影响比例。使f(.)不等于0，可以减少算法作偏向于纵深检查的可能性，使算法优先检索更靠近答案结点且又离根较近的结点。

LC-检索的特殊情况

• 
  

9.1.1 15-谜问题

定理9.1

判断15-谜问题能否由初始状态到达目标状态：

其中 LESS(X)和X的取值如下：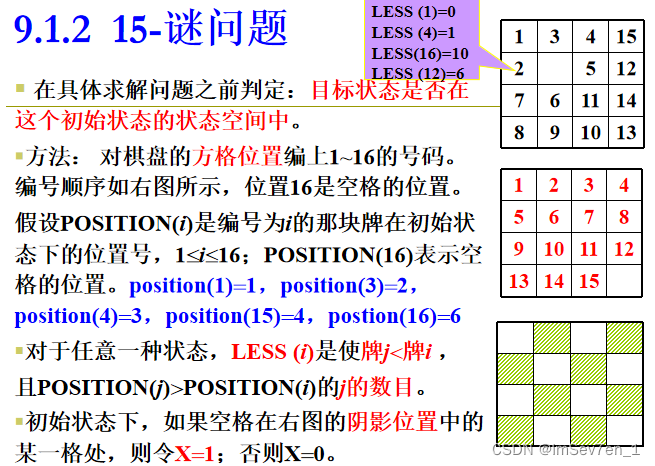

15-谜问题的求解方法

空白牌的移动顺序依次为：上、右、下、左

• 法1：FIFO检索

• 

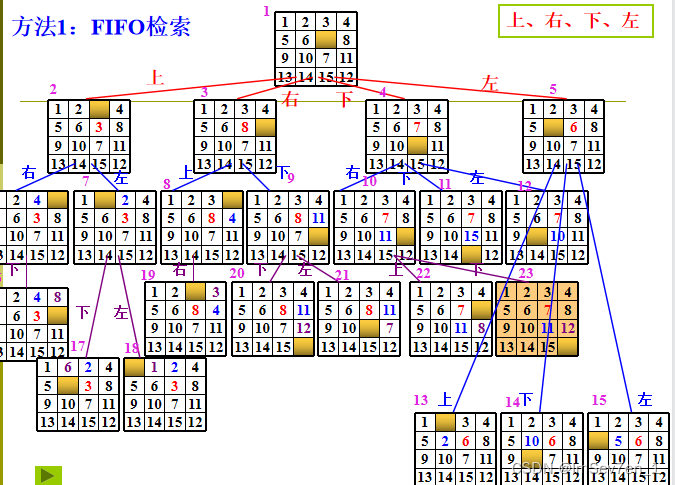
• 法2：深度优先检索

• 

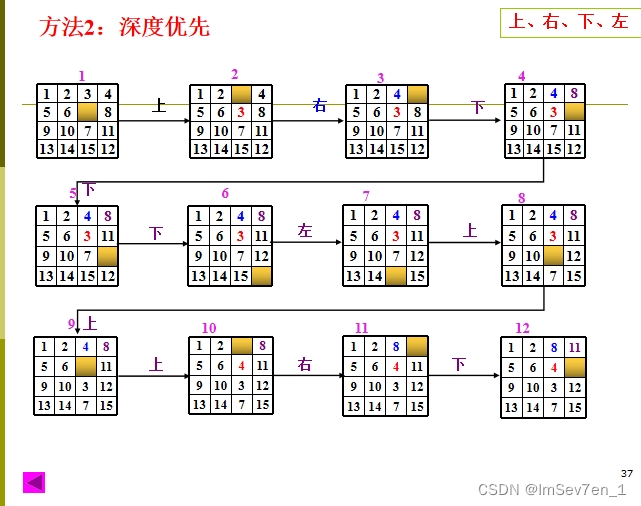
• 法3：LC检索

• 

• 

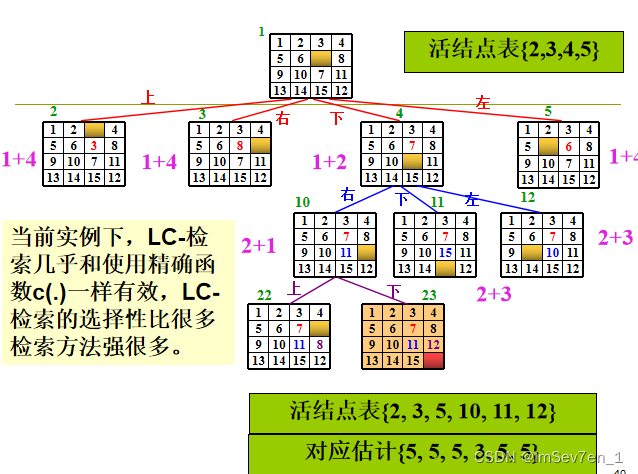
9.1.1 LC-检索的抽象化控制

c(.)、c(X)、c(T)
LC算法搜索一个答案结点，具体步骤：

算法9.1 LC-检索

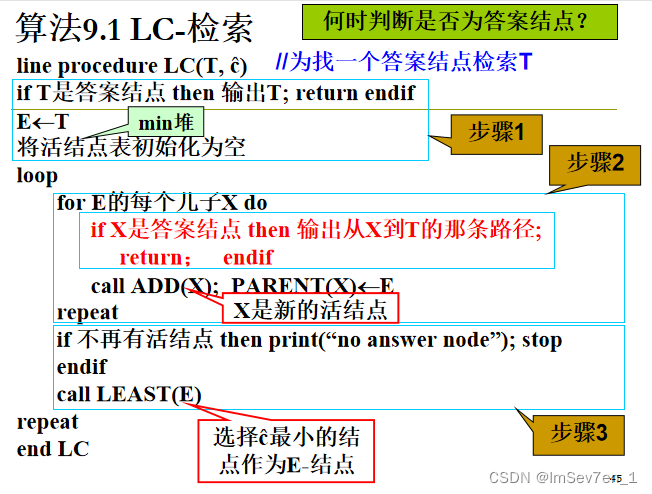
9.1.1 LC-检索的特性

定理9.2

理论上如何使得算法LC在到达一个最小成本的答案结点终止：
证明：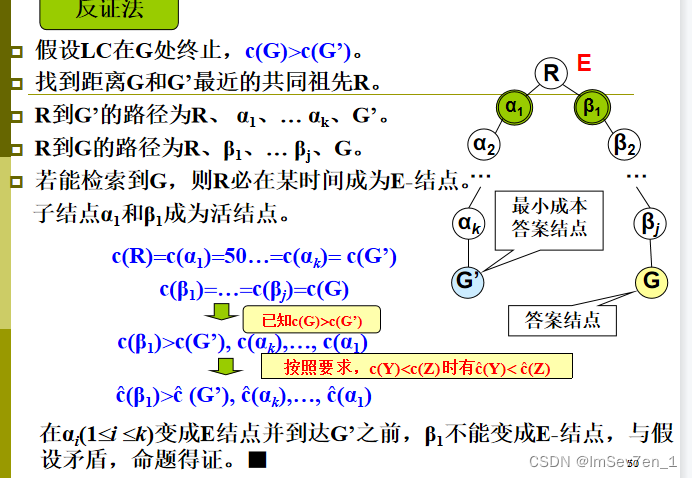

改进算法LC

上述的成本函数常常难以得到。

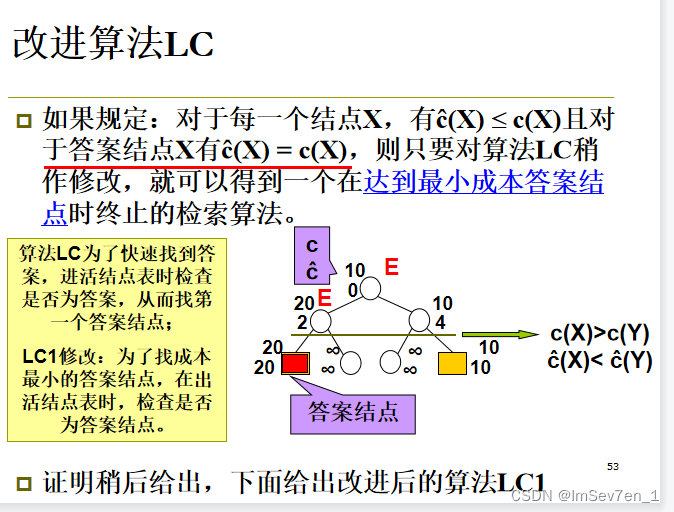
改进算法与LC算法不同之处

算法9.2 改进LC算法

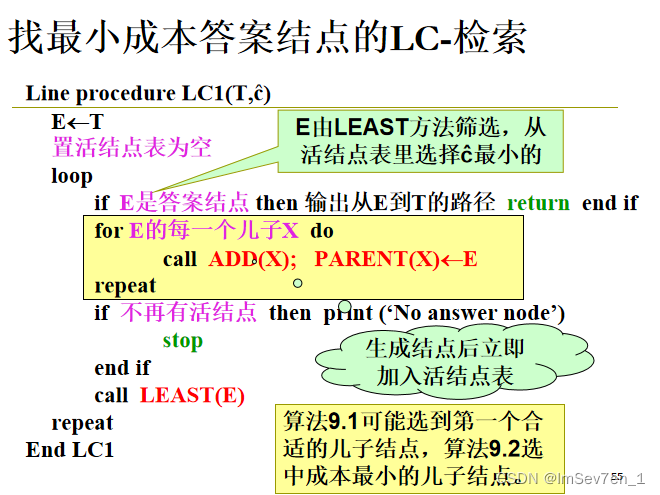
定理9.3

证明：

LC-检索的总结

分支限界与回溯的比较

分支限界法解决问题

带有限期的作业排序问题

问题描述：
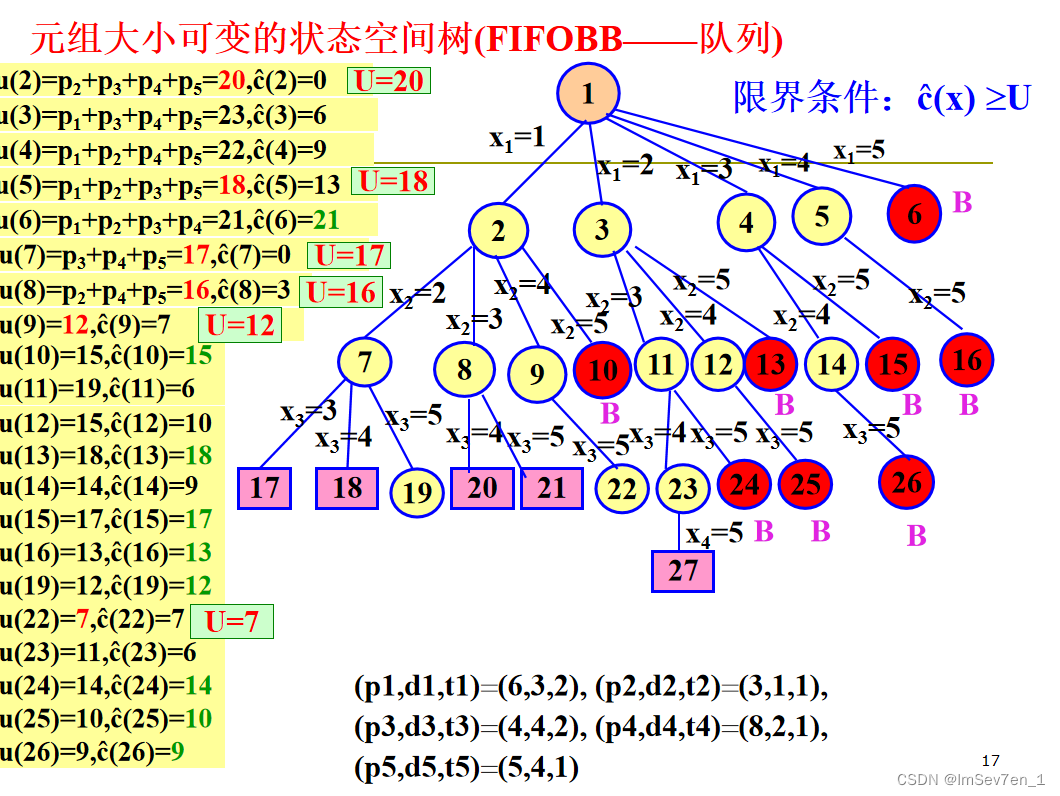
使用分支限界法，分别借助成本的估计函数ĉ (.)为c(X)的下界，同时设置最小成本的上界U（当前找到的最小成本），把ĉ(X) >U活结点杀死

简单说明，成本的估计函数ĉ (.)即为本应在Sx中但未在Sx中的作业罚款总和，上界u(x)为所有未在Sx中的作业罚款总和，U为所有u(x)中的最小值，注：所有结点在进入活结点表或出活结点表时候均需检查是否被限界（因为上界U不断在更新）
剪枝条件：c(X)>U

FIFOBB处理带有期限的作业问题

LIFOBB处理带有期限的作业问题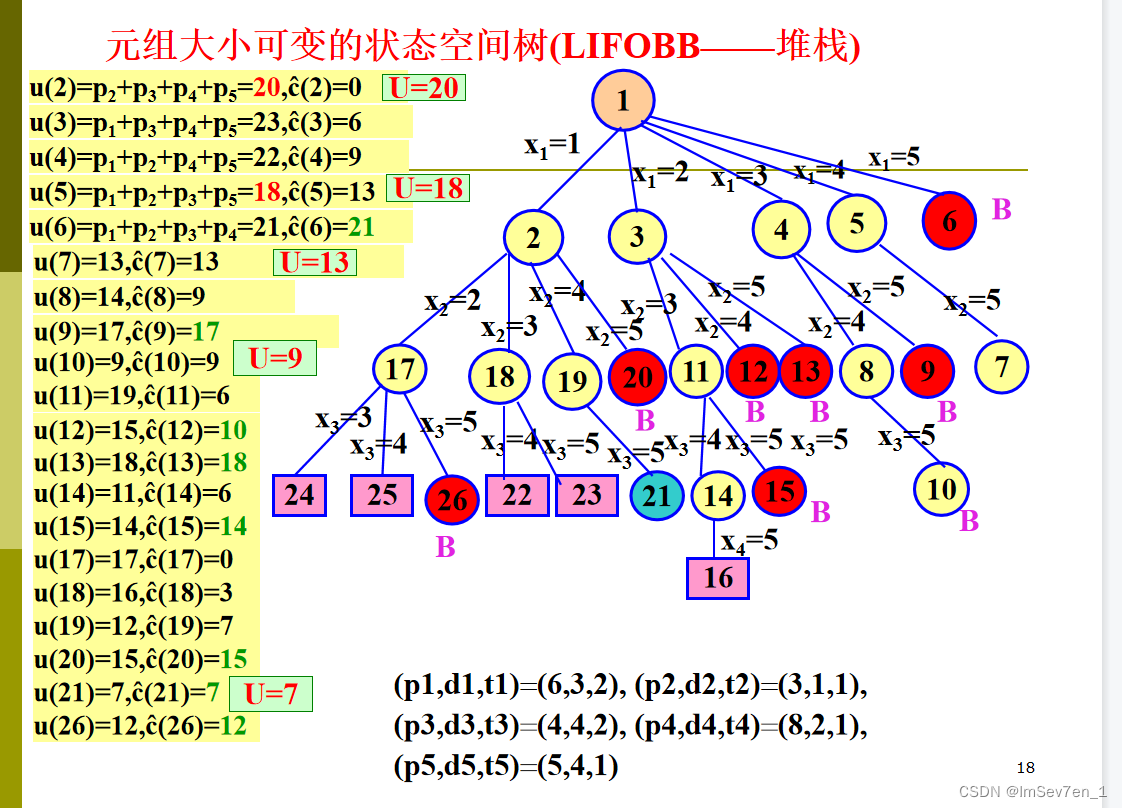

LCBB处理带有期限的作业问题

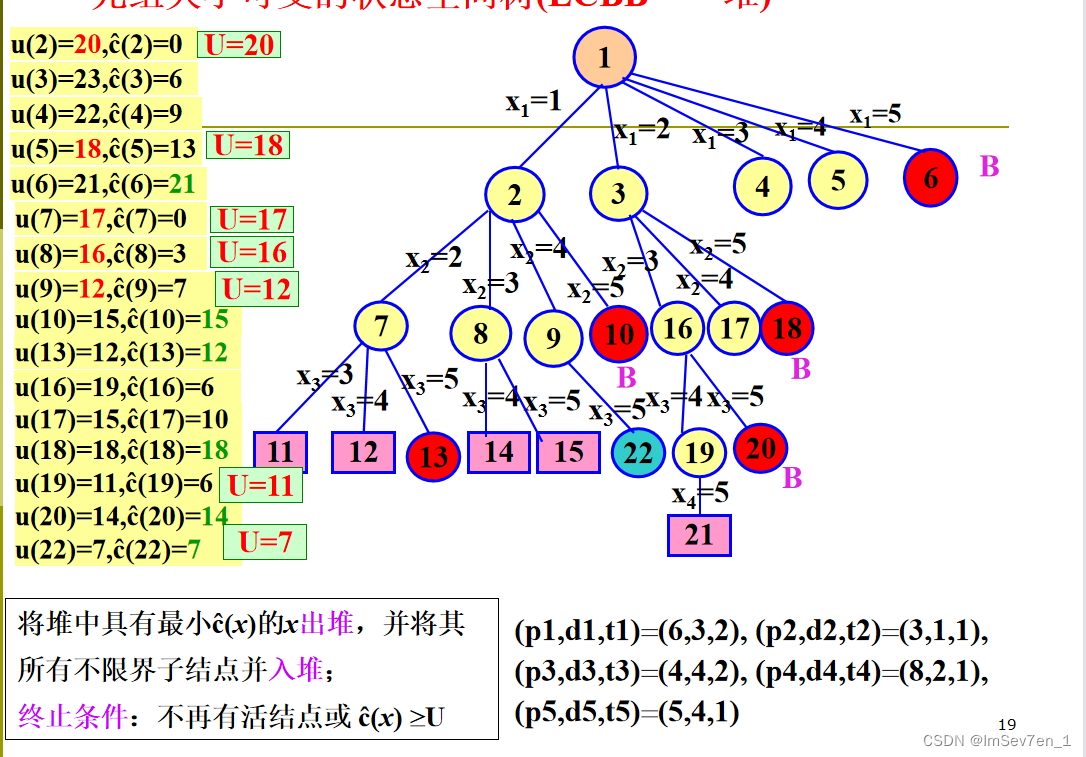
9.1.6效率分析

定理9.4

设U1和U2是状态空间树T最小成本答案结点的两个初始上界且U1<U2，那么FIFO，LIFO，和LC-分支限界算法在以U1为上界初始值时所生成的结点数不会多于以U2为上界初始值时所生成的结点数。

定理9.5

设U是状态空间树T最小成本答案结点的当前上界，由FIFO，LIFO，和LC-分支限界算法所生成的结点数不因拓展ĉ(X)>U的结点X而减少。

定理9.6

在FIFO，LIFO分支限界算法中使用一个更好的成本估计函数ĉ(.)不会增加其生成的结点数。

定理9.7

在LC-分支限界算法中使用一个更好的成本估计函数ĉ(.)可能会增加其生成的结点数。