这篇博客整理了离散数学部分的重要问答题,更偏向于二元关系与函数的理解,在面试时靠这个方向回答。
-
一、命题逻辑
- 什么是命题?
- 回答:命题是能判断真假的陈述句。例如,“3 是奇数” 是命题,其真值为真;而 “请把门关上” 不是命题,因为它不是陈述句。
- 什么是永真式、永假式和可满足式?
- 回答:若一个命题公式在所有赋值下取值均为真,则称该命题公式为重言式或永真式;若一个命题公式在所有赋值下取值均为假,则称该命题公式为矛盾式或永假式;若一个命题公式至少存在一组成真赋值,则称该命题公式为可满足式。例如,“p∨¬p” 是永真式,“p∧¬p” 是永假式,“p→q” 是可满足式。
- 怎样判断两命题公式等值?什么是等值演算?
- 什么是命题?
-
二、谓词逻辑
- 什么是指导变元,什么是自由出现和约束出现?
- 回答:在合式公式∀xA 和∃xA 中,称 x 为指导变项,A 为相应量词的辖域;x 的所有出现为约束出现,A 中不是约束出现的其他变项的出现为自由出现。例如,在公式∀x (P (x)→Q (x)) 中,x 是指导变元,P (x)→Q (x) 是辖域,x 在 P (x) 和 Q (x) 中的出现都是约束出现;而在公式∃xP (x)∧Q (y) 中,x 是指导变元,P (x) 是辖域,x 在 P (x) 中的出现是约束出现,y 在 Q (y) 中的出现是自由出现。
- 换名规则是什么?
- 回答:换名规则是将一个指导变项及其在辖域中所有约束出现替换成公式中没有出现的个体变项符号。例如,对于公式∀x (P (x)→Q (x)),可以将 x 换名为 y,得到∀y (P (y)→Q (y)),这两个公式是等值的。
- 什么是前束范式?
- 回答:设 A 为一谓词公式,如果 A 具有如下形式:Q1x1Q2x2…QkxkB,称 A 为前束范式,其中每个 Qi 为∀或∃,B 为不含量词的谓词公式。例如,∀x∃y (P (x,y)→Q (x,y)) 是前束范式,而∀x (P (x)→∃yQ (x,y)) 不是前束范式,但可以通过等值演算将其化为前束范式。
- 什么是指导变元,什么是自由出现和约束出现?
-
三、集合的基本概念和运算
- 什么是幂集?
- 回答:设 A 为集合,把 A 的全体子集构成的集合称作 A 的幂集,记作 P (A)。例如,若 A={1,2},则 P (A)={∅,{1},{2},{1,2}}。幂集的元素个数为 2 的集合 A 的元素个数次方,即 | P (A)| = 2^|A|。
- 证明集合恒等式的方法有哪些?
- 回答:证明集合恒等式的方法有命题演算法(两个方向的包含)、恒等变形法、反证法等。例如,要证明 A∪(B∩C)=(A∪B)∩(A∪C),可以使用命题演算法,分别证明 A∪(B∩C)⊆(A∪B)∩(A∪C) 和 (A∪B)∩(A∪C)⊆A∪(B∩C);也可以使用恒等变形法,根据集合运算的基本算律对等式两边进行变形,直到得到相同的表达式;还可以使用反证法,假设等式不成立,然后推出矛盾。
- 什么是幂集?
-
四、二元关系与函数(重要)
- 什么是集合的笛卡尔积?
- 回答:设 A,B 为两个集合,用 A 中元素作为第一元素,B 中元素为第二元素都成有序对。所有这样的有序对组成的集合为 A 和 B 的笛卡尔积,记作 A×B。例如,若 A={1,2},B={a,b},则 A×B={(1,a),(1,b),(2,a),(2,b)}。笛卡尔积的元素个数为集合 A 的元素个数乘以集合 B 的元素个数,即 | A×B| = |A|×|B|。
- 什么是二元关系?
- 回答:如果一个集合为空集或者它的元素都是有序对,则称这个集合是一个二元关系,一般记作 R。例如,在集合 A={1,2,3} 上的小于关系 R={(1,2),(1,3),(2,3)},就是一个二元关系。
- 如何表示二元关系?
- 回答:二元关系可以用集合表达式、关系矩阵、关系图来表示。例如,对于集合 A={1,2,3} 上的关系 R={(1,2),(2,3),(3,1)},其集合表达式为 R={(1,2),(2,3),(3,1)};关系矩阵为 MR = [0 1 0; 0 0 1; 1 0 0];关系图为以 1,2,3 为顶点,有向边分别为 (1,2),(2,3),(3,1) 的图。
- 介绍关系的性质。
- 回答:关系的性质包括自反性、反自反性、对称性、反对称性、传递性。对于给定集合A中的关系R,
- 自反性是指对于集合 A 中的任意元素 x,都有 (x,x)∈R,关系矩阵的特点是主对角线元素全为1,关系图的特点是每一顶点都有环;
- 反自反性是指对于集合 A 中的任意元素 x,都有 (x,x)∉R;关系矩阵的特点是主对角线元素全为0,关系图的特点是每一个顶点都没有环;
- 对称性是指对于集合 A 中的任意元素 x 和 y,如果 (x,y)∈R,则 (y,x)∈R;关系矩阵的特点是矩阵沿主对角线对称,关系图的特点是若两个顶点之间有边,则一定是一对方向相反的边;
- 反对称性是指对于集合 A 中的任意元素 x 和 y,如果 (x,y)∈R 且x≠y,则 (y,x)∉R;关系矩阵的特点是如果一个元素等于1,并且这个元素不是对角线上的元素,那么这个元素的行标列标互换的话,其值等于0;关系图的特点是若两个顶点之间有边,则一定是一条有向边;
- 传递性是指对于集合 A 中的任意元素 x、y 和 z,如果 (x,y)∈R 且 (y,z)∈R,则 (x,z)∈R。关系图的特点是若顶点xi到xj有边且xj到xk有边,则xi到xk有边。
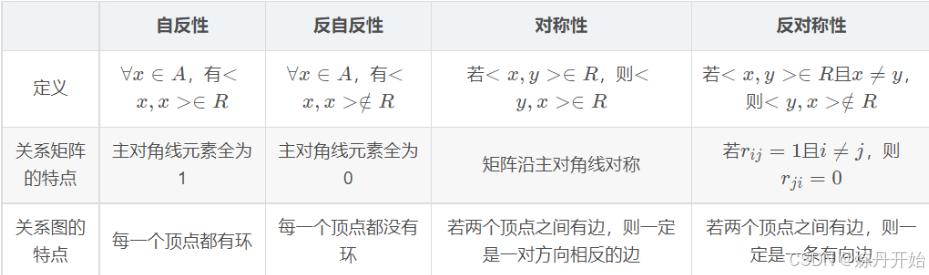
- 回答:关系的性质包括自反性、反自反性、对称性、反对称性、传递性。对于给定集合A中的关系R,
- 介绍关系的自反(对称,传递)闭包,以及如何求各闭包?
- 回答:x
- 什么是集合上的等价关系?
- 回答:设 R 为非空集合 A 上的关系,如果 R 是自反的,对称的和传递的,则称 R 为 A 上的等价关系。例如,在整数集上的模 n 同余关系。
- 什么是等价类和商集?
- 回答:设 R 是非空集合 A 上的等价关系,A上相互等价元素构成的若干个子集就是等价类。 任何等价类就是集合A的非空子集,所有等价类的并集就是A。
- 什么是集合上的偏序关系?
- 回答:设 R 为非空集合 A 上的关系,如果 R 是自反的,反对称的和传递的,则称 R 为 A 上的偏序关系。例如,实数集上的小于等于关系≤、集合的包含关系⊆都是偏序关系。
- 什么是偏序集,什么是全序集?
- 回答:一个集合 A 和 A 上的偏序关系 R 一起被称作偏序集,记作 <A,R>。
- 如何描述偏序集?
- 回答:对于有穷的偏序集 <A,≤> 可以用哈斯图来描述,实际上哈斯图是简化的关系图,在哈斯图中每个结点表示 A 中的一个元素,结点位置按他们在偏序中的次序从底向上排列。
- 介绍集合的最小元,最大元,极小元,极大元的概念。
- 回答:设 <B,≤> 是偏序集,B 是 A 的子集。
- 若对任意 x∈B,都有 b≤x,则称 b 为 B 的最小元;
- 若对任意 x∈B,都有 x≤b,则称 b 为 B 的最大元;
- 极小元、极大元就是可以取到的那个元素。
- 介绍集合的上界,下界,上确界,下确界的概念。
- 回答:x
- 介绍下列函数的性质:满射,单射,双射。
- 回答:设函数f:A->B (读作:设函数f 是从A到B的函数)(B为陪域,f(A)值域)
(1)函数的值域等于陪域,则称f是满射的;
(2)若对于任何的x1,x2∈A,x1≠x2,都有f(x1)≠f(x2),则称f是单射的;
(3)若f既是满射的又是单射的,则称f是双射的。
- 回答:设函数f:A->B (读作:设函数f 是从A到B的函数)(B为陪域,f(A)值域)
- 什么是集合的笛卡尔积?
-
五、图(重要)
- 简述并证明握手定理。
- 回答:握手定理是指任何图中所有顶点的度数之和等于边数的 2 倍。
- 图的几种矩阵表示
- 答:
- 关联矩阵(表示的是点和边关联的关系,对于无向图,点和边关联值为1,不关联就为-1)
- 邻接矩阵(表示的是点和点邻接的关系,有边相连就为1,无边相连就为0)
- 可达矩阵(是邻接矩阵的plus版,表示的不仅是点和点的邻接关系,还表示了某个点是否可以到达另一个点,点到点能到达就为1,否则为0)
- 简述并证明握手定理。
 离散数学重要问答整理
离散数学重要问答整理





















 1066
1066

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








