AcWing 第 57 场周赛

最新推荐文章于 2025-12-20 17:21:30 发布

原创最新推荐文章于 2025-12-20 17:21:30 发布 · 315 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #图论 #c++

算法竞赛专栏收录该内容

31 篇文章

订阅专栏

这篇博客探讨了两个数学问题。第一个问题是对比两个数组元素之和的大小，通过读取并累加数组元素来判断。第二个问题涉及对整数进行一系列操作，包括乘以任意正整数和开平方，寻找最小可能值和所需操作次数。解决这个问题的关键在于质因数分解，通过试除法找到所有质因子及其指数，然后利用操作减少质因子的次数。

4485. 比大小

给定一个长度为 n 的数组 a1,a2,…,an 和一个长度为 n 的数组 b1,b2,…,bn。

请你计算，数组 a 的所有元素之和是否大于或等于数组 b 的所有元素之和。

输入格式
第一行包含整数 n。

第二行包含 n 个整数 a1,a2,…,an。

第三行包含 n 个整数 b1,b2,…,bn。

输出格式
如果数组 a 的所有元素之和大于或等于数组 b 的所有元素之和，则输出 Yes，否则输出 No。

数据范围
前三个测试点满足 1≤n≤5。
所有测试点满足 1≤n≤50，0≤ai,bi≤1000。

输入样例1：
5
1 2 3 4 5
2 1 4 3 5
输出样例1：
Yes
输入样例2：
5
1 1 1 1 1
1 0 1 0 1
输出样例2：
Yes
输入样例3：
3
2 3 9
1 7 9
输出样例3：
No

签到

// Author: Changersh
// Problem: 比大小
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/4488/
// When: 2022-06-29 14:28:38
// 
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 


#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include<tr1/unordered_map>
#include <tr1/unordered_set>

using namespace std::tr1;
using namespace std;
typedef long long ll;
const int N = 5e4 + 50;
const int MOD = 1e9 + 7;

int n, a, b, sum1, sum2;
int main() {
	// scanf("%d", &T);while (T--)solve();
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d", &a);
		sum1 += a;
	}
	for (int i = 0; i < n; i++) {
		scanf("%d", &b);
		sum2 += b;
	}
	if (sum1 >= sum2)printf("Yes\n");
	else printf("No\n");
	return 0;
}

4486. 数字操作

给定一个整数 n，你可以对该数进行任意次（可以是 0 次）变换操作。

每次操作为以下两种之一：

将整数 n 乘以任意一个正整数 x。
将整数 n 替换为 n√（执行此操作的前提是 n√ 为整数）。
请你计算，通过上述操作，n 能达到的最小可能值，以及达到最小可能值所需要的最少操作次数。

输入格式
一个整数 n。

输出格式
一行，两个整数，分别为 n 能达到的最小可能值，以及达到最小可能值所需要的最少操作次数。

数据范围
所有测试点满足 1≤n≤106。

输入样例1：
20
输出样例1：
10 2
输入样例2：
5184
输出样例2：
6 4

数论分解质因子

质因数分解定理：一个数可以分解成它的质因子的不同/相同次方的乘积
两种操作，一个是乘以一个数x，这个不会改变质因子的种类数
二是开平方，其实就是每个质因子的次数都除以二，也不会改变质因子的种类数
所以最小的可能值就是所有质因子的乘积。

取一个 2^m，大于所有的次数，因为操作二，开根号其实就是所有质因子次数除以二而已。

又在需要乘的每一步都乘一下 x 其实等于最开始先乘一个总的 x ，这样步数少，所以把它放在第一步
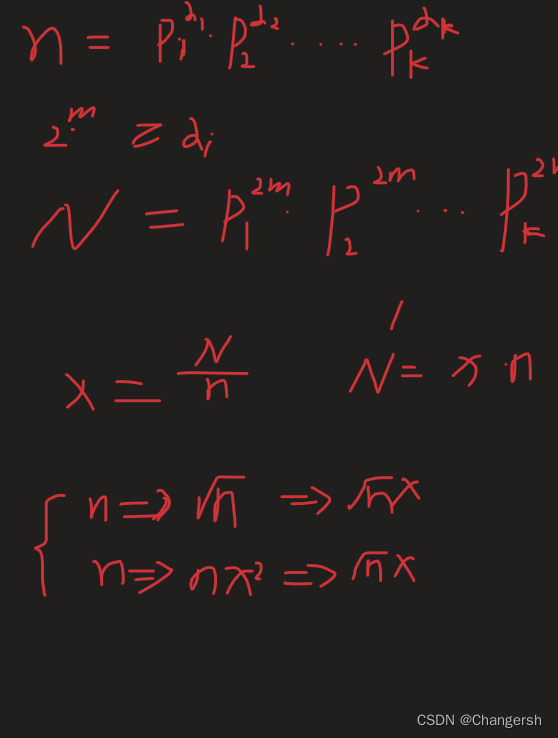
在这里插入图片描述

其实次数就是 m 的值，因为你要开二次根号，开m次。
用试除法求质因子，记得把质因子除尽，计算出当前质因子的指数，2^m>= 最大的指数。
之后，如果n>1，说明 n 本身就是自己的质因子，指数是 1 .
前面这个内容等于是默认所有的质因子指数都一样，但是一般是不一样的，只要有一个质因子小于 2^m，就代表这个n 小于我们构造出来的N，所以需要乘以一个总的 X，步数 + 1，m++

// Author: Changersh
// Problem: 数字操作
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/4489/
// When: 2022-06-29 14:58:27
//
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <map>
#include <set>
#include <string>
#include <tr1/unordered_map>
#include <tr1/unordered_set>
#include <vector>

using namespace std::tr1;
using namespace std;
typedef long long ll;
const int N = 5e4 + 50;
const int MOD = 1e9 + 7;

// 分解质因子

int main() {
  int n;
  scanf("%d", &n);
  vector<int> s;  // 存质因子的次数
  int res = 1;
  int m = 0; // 最高次数应该小于等于 2的整数次方
  // 试除法分解质因子
  for (int i = 2; i * i <= n; i++) {
    if (n % i == 0) {
    	int c = 0;  // 次数
    	while (n % i == 0) n /= i, c++;
    	res *= i; // 结果
    	s.push_back(c);
    	while (1 << m < c) m++;
    }
  }
  if (n > 1) { // 说明 n 是质数
  	res *= n;
  	s.push_back(1);
  	while (1 << m < 1) m++;
  }
  for (auto x : s) {
  	if (x < 1 << m) {
  		m++;
  		break;
  	}
  }
	printf("%d %d", res, m);
	
	
  return 0;
}