Python复变函数多值函数的直观表现_python绘制复变函数-优快云博客

本文链接：https://blog.youkuaiyun.com/Chandler_river/article/details/126862264

该博客介绍了如何使用Python进行复变函数的可视化，特别是根式函数的动态展示。作者通过创建一个`complex_number`类来表示复数，并提供了一个`fun`函数用于绘制复数轨迹。`Shine`函数则实现了根式函数的分支映射。博客还展示了如何用matplotlib创建动画效果，尽管作者提到自己不擅长此领域。代码示例中，`start`变量定义了复数起点，`R_step`控制半径增加量，而`Shine`函数的参数`k`决定了开方的次数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

好习惯，讲问题先上效果图

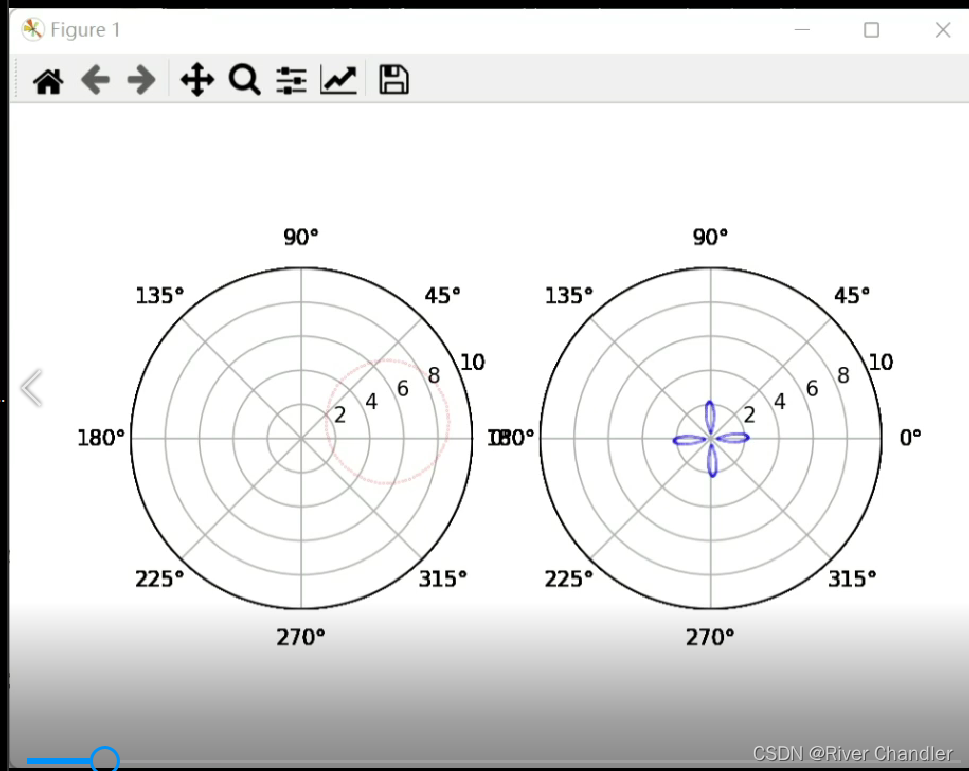
你问博主为什么不把它整成一个动画，简单，博主不会

好习惯二讲问题先上全部代码

#复变函数的可视化  根式函数的可视化
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation
import numpy as np
import multiprocessing as mp

#tip1:Github 上有很好的例子
#tip2:Python 中是有complex()这个函数的
#tip3:正经人谁搞个复数还要面向对象......
#tip4:数理方法，笑死，根本不懂
#tip5:复变函数是复平面到复平面的对应
     #如果你想实现如实变函数一样的效果 什么(z-z**2)**1.5+z*(z*0.5)
     #可能略有难度...

     
class complex_number():

    def __init__(self,Mod,Arg):
        self.Mod = Mod
        self.Arg = Arg


def fun(R,steps=100):
    global start
    d_theta = 2*np.pi/steps
    this_list = []
    for step in range(steps):
        theta = step * d_theta
        x,y = start[0]+R*np.cos(theta),start[1]+R*np.sin(theta)
        r = (x**2+y**2)**0.5
        t = np.arctan(y/x)
        if x<0:
            t = t + np.pi
        this_list.append(complex_number(r,t))

    ax1 = fig.add_subplot(1,2,1,projection="polar")
    ax1.set_ylim([0,10])
    for i in this_list:
        plt.polar(i.Arg,i.Mod,"ro",ms=0.1)
        
    return this_list

def Shine(this_list,k=2):
    shine_dict = {}     #shine 表示映射

    for i in range(k):  #为什么是k呢，根式函数开几次方就几个branch 你要问1.5次方呢？综值的问题吧
        shine_dict[i] = []   #这叫做提前分配内存  虽然我们不太可呢遇上什么 开50000次方的问题
    shine_dict["Mod_list"] = [] #但这是好习惯

    ax2 = fig.add_subplot(1,2,2,projection="polar")
    ax2.set_ylim([0,10])
    for this in this_list:
        args = [this.Arg/k+i*2*np.pi/k for i in range(k)]
        shine_dict["Mod_list"].append(this.Mod/k)
        shine_dict[this_list.index(this)] = args

        for ARG in args:
            plt.polar(ARG,this.Mod/k,"bo",ms=0.1)
        

if __name__ == "__main__":
    frames = []
    start = [5,1]
    R_range = [0.1,0.7]
    R_step = 0.2
    fig = plt.figure()
    for i in range(100):
        Shine(fun(0.2+i*R_step),4)
        plt.pause(0.1)