11-411/611NLP Lecture 4.Words and Morphology

Morphology(形态学)

words are not atoms

单词并不是语言的最小单位，它们由更深的内部结构语素(Morphems)构成。

单词就好比化学中的分子虽然是一个整体，而但可以将其拆分为原子，而语素就是够成它的原子。
[example]

• mis-undersatnd-ing-s
• 同志们

Morphemes(语素)

Concatenative morphology(毗邻语素)

每个单词由若干语素毗邻组成

• Roots(词根)
  • 单词的中心语素，是单词的含义
• Affixes(词缀)
  • Prefixes(前缀)
    • pre-nuptual
    • ir-regular
  • Suffixes(后缀)
    • determin-ize
    • iterat-or
  • Infixes(中缀)
    • Pennsyl-f**kin-vanian
  • Circumfixes(位缀)
    • ge-sammel-t

Nonconcatenative morphology(非毗邻语素)

• Umlaut(元音变音)
  • foot:feet
  • tooth:teeth
• Ablaut(元音变换)
  • sing:sang:sung
• Root-and-pattern morphology(词根与模式语素) or templatic morphology(模板语素)
  • 常见于Arabic(阿拉伯),Hebrew(希伯来),other Afroasiatic(亚非语系)语言中
  • 辅音构成词根，再推入元音
• Infixation(中缀)
  • Gr-um-adwet

Words(词)

语素构成单词的方法主要为两类：inflrction(屈折)、derivation(派生)。

Inflectional morphology(屈折形态学)

将与上下文相关的信息添加到单词中。这类词之间一般语义相同。
例如上下文中名词的数量、动词的第三人称单数形式等,在句子中表示主谓宾位置的变化等。
[example]

• Number(singular versus plural)
  • automaton:automata
  • walk:walks
• Case(nominative versus accusative versus…)
  • he:him:his…

Derivation morphology(派生形态学)

将单词与词缀组合构成新词。这类词之间一般语义不同。
[example]

• parse:parse
• repulse:repulsive

Irregularity(不规则性)

屈折形态一般与其词根有关
相同的派生词素根据它所依附的词根可能具有不同的含义与功能

• Formal irregularity(形式不规则)
  • walk:walked:walked
  • sing:sang:sung
• Semantic irregularity/unpredictability(语义不规则/不可测)
  • a king-ly old man(使用正确)
  • a slow-ly old man(使用错误)

Finite State Transducers(有穷状态转换器)

Finati State Automata(有穷状态自动机)

正则语言(regular language)：能被FSA识别的语言。大多数自然语言都能被表示为正则语言。
形式语言(formal lauguage)：一种能被自动机生成或识别的不同于自然语言的语言

• Q：a finite set of states(有穷状态集)
• $q_0$∈Q：a special start state(特殊的开始状态)
• F$\subseteq$Q：a set of final states(结束状态集，是Q的子集)
• $\Sigma$：a finite alphabet(有穷字母集)
• Trancitions(过渡)：
  
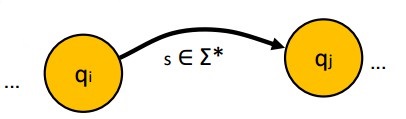
• Encodes a set of strings that can be recongnized by following paths from $q_0$ to some state in F.

[example]
关于羊的语言‘baaaa!’的FSA识别过程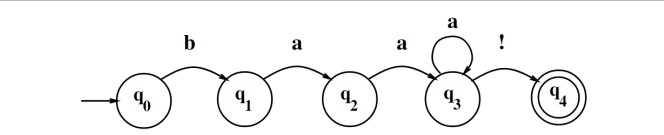
它可以识别

baa!
baaa!
baaaa!
...

对应的正则表达式为’baa+!’

[example]
FSA for English Derivational Morphology

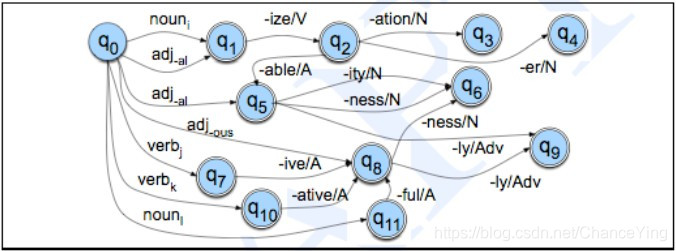
FSAs and regular expressions(正则表达式)

• 正则表达式是描述FSA的一种方法
• 任何正则表达式都可以用FSA来实现
• 任何FSA都可以用正则表达式来描述

在某些编程语言(如Perl、Python)中出现的正则表达式的功能经常超越了真正的正则表达式

Morphology Parsing(形态剖析)

输入：单词
输出：由其他语素表达的词干、特征
[example]

• geese: {goose+N+PI}
• gooses: {goose+V+3P+Sg}
• dog: {dog+N+Sg, dog+V}
• leaves: {leaf+N+PI, leave+V+3P+Sg}

形态分析方法

• Table(查表)
  • 优点：快速查找
  • 缺点：占用空间大，建立数据库消耗资源大
• Trie(字典树)
  • 优点：灵活性高
  • 缺点：冗余高
• Final-state transducer(有穷状态转换机)

Finite State Transducers(有穷状态转换器)

• Q：a finite set of states(有穷状态集)
• $q_0\in$Q：a special start state(特殊的开始状态)
• F$\subseteq$Q：a set of final states(终止状态集，是Q的子集)
• $\Sigma$ and $\Delta$：two finite alphabets(两个有穷字母集)
• Transitions(过渡)：
  
  [example]
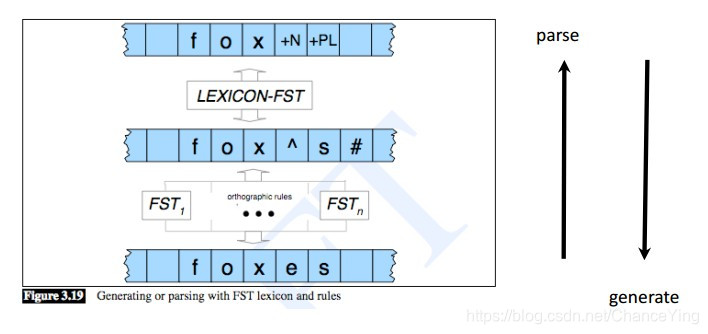
  通过FSTs进行的形态分析
  
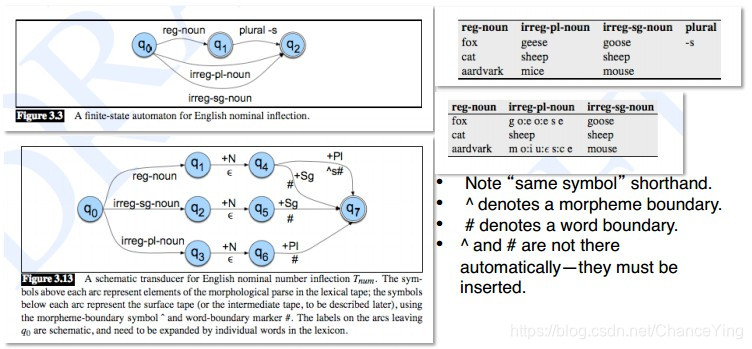
  形态分析器(morphological analyzer)的构成
• Morphotactics(形态顺序规则)
  • 建立语素间顺序的模型与映射
• Allomorphic rules(同构规则)
  • 建立词汇层与表层的映射。如，“zoch^s#” <-> “zoches”
• orthographic rule(正词法规则)
  • 

[example]
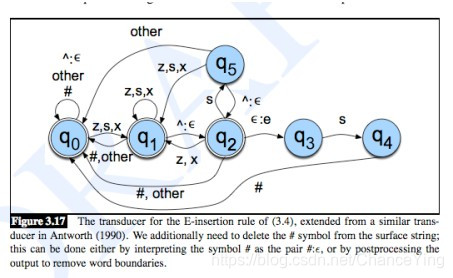
一个关于E Insertion rule的FST例子

$ϵ⟶e/\left\{\begin{array}{c}s\\ x\\ z\end{array}\right\}$^___s#

FST and FSA

FSA的主要表现形式是正则表达式，用于识别(recongnize) 语言。
FST不仅可以识别语言，还能产生(generates) 语言。分析(parse)输入、转化(transform)文字为新的形式

Stemming(词干提取)

Input: a word
Output: the word’s stem (approximately)
[example]

• -sses$\to$-ss
• -ies$\to$-i
• -ss$\to$-s
  

Tokenization(分词)

Input: raw text
Output: sequence of tokens normalized for easier processing

Algorithem(算法)

Weighted Finite State Transducers